Codeforces Round #498 (Div. 3）ABCDE

A 签到

奇数不变，偶数减一

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+10;
int n, a[N], b[N], tot;
int M = 1e9;
int main() {
    cin >> n;
    for(int i = 0; i < n; i ++) {
        cin >> a[i];
    }
    for(int i = 0; i < n; i ++) {
        if(a[i]&1) printf("%d ",a[i]);
        else printf("%d ",a[i]-1);
    }
    return 0;
}

B. Polycarp's Practice

n个数，去k个区间，是的区间的最大值之和最大。

直接去最大的k个数就行。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+10;
int n, k, a[N], x;
struct Nod{
    int id, num;
}e[N];
bool cmp(Nod a, Nod b) {
    return a.num > b.num;
}
int main() {
    cin >> n >> k;
    for(int i = 1; i <= n; i ++) {
        cin >> x;    
        e[i].id = i;
        e[i].num = x;
    }
    sort(e+1,e+1+n,cmp);
    int ans = 0;
    for(int i = 1; i <= k; i ++) {
        a[i] = e[i].id;
        ans += e[i].num;
    }
    printf("%d
",ans);
    if(k==1) return 0*printf("%d
",n);
    sort(a+1,a+1+k);
    for(int i = 1; i < k; i ++) {
        printf("%d ",a[i]-a[i-1]);
    }
    printf("%d
",n-a[k-1]);
    return 0;
}

C. Three Parts of the Array

n个数，划分为三个区间，可以为空，求第一个区间之和与第三区间之和相同时，最大值是多少。

1至n，遍历下，求出前i个数之和，判断是否[j,n]之和等于前面的就行，二分查找。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5+10;
ll n, a[N], sum[N], pre[N];
bool ok(int l, int r, ll cnt) {
    while(l <= r) {
        int m = (l+r) >> 1;
        if(pre[m] == cnt) return true;
        if(pre[m] > cnt) l = m+1;
        else r = m-1;
    }
    return false;
}
int main() {
    cin >> n;
    for(int i = 1; i <= n; i ++) {
        cin >> a[i];
        sum[i] = sum[i-1] + a[i];
    }
    for(int i = n; i >= 0; i --) pre[i] = pre[i+1] + a[i];
    ll MAX = 0;
    for(int i = 1; i <= n; i ++) {
        ll ans = sum[i];
        if(ok(i+1,n, ans)) {
            MAX = ans;
        }
    }
    printf("%lld
",MAX);
    return 0;
}

D. Two Strings Swaps

You are given two strings $\mathrm{aa and bb consisting\; of\; lowercase\; English\; letters,\; both\; of\; length nn.\; The\; characters\; of\; both\; strings\; have\; indices\; from 11 to nn,\; inclusive.}$

You are allowed to do the following changes:

• Choose any index $\mathrm{ii (1\le i\le n1\le i\le n)\; and\; swap\; characters aiai and bibi;}$
• Choose any index $\mathrm{ii (1\le i\le n1\le i\le n)\; and\; swap\; characters aiai and an-i+1an-i+1;}$
• Choose any index $\mathrm{ii (1\le i\le n1\le i\le n)\; and\; swap\; characters bibi and bn-i+1bn-i+1.}$

Note that if $\mathrm{nn is\; odd,\; you\; are\; formally\; allowed\; to\; swap a\lceil n2\rceil a\lceil n2\rceil with a\lceil n2\rceil a\lceil n2\rceil (and\; the\; same\; with\; the\; string bb)\; but\; this\; move\; is\; useless.\; Also\; you\; can\; swap\; two\; equal\; characters\; but\; this\; operation\; is\; useless\; as\; well.}$

You have to make these strings equal by applying any number of changes described above, in any order. But it is obvious that it may be impossible to make two strings equal by these swaps.

In one preprocess move you can replace a character in $\mathrm{aa with\; another\; character.\; In\; other\; words,\; in\; a\; single preprocess\; move you\; can\; choose\; any\; index ii (1\le i\le n1\le i\le n),\; any\; character cc and\; set ai:=cai:=c.}$

Your task is to find the minimum number of preprocess moves to apply in such a way that after them you can make strings $\mathrm{aa and bb equal\; by\; applying\; some\; number\; of changes described\; in\; the\; list\; above.}$

Note that the number of changes you make after the preprocess moves does not matter. Also note that you cannot apply preprocess movesto the string $\mathrm{bb or\; make\; any preprocess\; moves after\; the\; first change is\; made.}$

Input

The first line of the input contains one integer $\mathrm{nn (1\le n\le 1051\le n\le 105)\; —\; the\; length\; of\; strings aa and bb.}$

The second line contains the string $\mathrm{aa consisting\; of\; exactly nn lowercase\; English\; letters.}$

The third line contains the string $\mathrm{bb consisting\; of\; exactly nn lowercase\; English\; letters.}$

Output

Print a single integer — the minimum number of preprocess moves to apply before changes, so that it is possible to make the string $\mathrm{aa equal\; to\; string bb with\; a\; sequence\; of changes from\; the\; list\; above.}$

Examples

input

Copy

7
abacaba
bacabaa

output

Copy

4

input

Copy

5
zcabd
dbacz

output

Copy

0

Note

In the first example preprocess moves are as follows: ${\mathrm{a1:=a1:=\text{'}b\text{'}, a3:=a3:=\text{'}c\text{'}, a4:=a4:=\text{'}a\text{'}\; and a5:=a5:=\text{'}b\text{'}.\; Afterwards, a=a="bbcabba".\; Then\; we\; can\; obtain\; equal\; strings\; by\; the\; following\; sequence\; of changes: swap(a2,b2)swap(a2,b2) and swap(a2,a6)swap(a2,a6).\; There\; is\; no\; way\; to\; use\; fewer\; than 44preprocess\; moves before\; a\; sequence\; of changes to\; make\; string\; equal,\; so\; the\; answer\; in\; this\; example\; is 44.}}^{}$

In the second example no preprocess moves are required. We can use the following sequence of changes to make $\mathrm{aa and bb equal: swap(b1,b5)swap(b1,b5), swap(a2,a4)swap(a2,a4).}$

$\mathrm{两个长度为n的字符串，需要让两个字符串变成相同时的最小修改数。有三个操作和一个修改。}$

$\mathrm{1、交换ai与bi}$

$\mathrm{2、交换ai与an-i+1}$

$\mathrm{3、交换bi与bn-i+1}$

$\mathrm{将ai修改成任意字符}$

有几种情况，

当为 a a   不需要改变   a c   改变一次    a a   改变两次

        b b                        b a                     b c 

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5+10;
int n;
set<char> st;
char str1[N], str2[N];
int main() {
    cin >> n >> str1+1 >> str2+1;
    int ans = 0;
    for(int i = 1, j = n; i < j; i ++, j--) {
        int now = min((str1[i]!=str2[i])+(str1[j]!=str2[j]), (str1[i]!=str2[j])+(str1[j]!=str2[i]));
        if(str2[i]==str2[j]) now = min(now, int(str1[i]!=str1[j]));
        ans += now;
    }
    ans += (n%2==1&&str1[(n+1)/2]!=str2[(n+1)/2]);
    printf("%d
",ans);
    return 0;
}

E. Military Problem

In this problem you will have to help Berland army with organizing their command delivery system.

There are $\mathrm{nn officers\; in\; Berland\; army.\; The\; first\; officer\; is\; the\; commander\; of\; the\; army,\; and\; he\; does\; not\; have\; any\; superiors.\; Every\; other\; officer\; has\; exactly\; one\; direct\; superior.\; If\; officer aa is\; the\; direct\; superior\; of\; officer bb,\; then\; we\; also\; can\; say\; that\; officer bb is\; a\; direct\; subordinate\; of\; officer aa.}$

Officer $\mathrm{xx is\; considered\; to\; be\; a\; subordinate\; (direct\; or\; indirect)\; of\; officer yy if\; one\; of\; the\; following\; conditions\; holds:}$

• officer $\mathrm{yy is\; the\; direct\; superior\; of\; officer xx;}$
• the direct superior of officer $\mathrm{xx is\; a\; subordinate\; of\; officer yy.}$

For example, on the picture below the subordinates of the officer $\mathrm{33 are: 5,6,7,8,95,6,7,8,9.}$

The structure of Berland army is organized in such a way that every officer, except for the commander, is a subordinate of the commander of the army.

Formally, let's represent Berland army as a tree consisting of $\mathrm{nn vertices,\; in\; which\; vertex uu corresponds\; to\; officer uu.\; The\; parent\; of\; vertex uucorresponds\; to\; the\; direct\; superior\; of\; officer uu.\; The\; root\; (which\; has\; index 11)\; corresponds\; to\; the\; commander\; of\; the\; army.}$

Berland War Ministry has ordered you to give answers on $\mathrm{qq queries,\; the ii-th\; query\; is\; given\; as (ui,ki)(ui,ki),\; where uiui is\; some\; officer,\; and kiki is\; a\; positive\; integer.}$

To process the $\mathrm{ii-th\; query\; imagine\; how\; a\; command\; from uiui spreads\; to\; the\; subordinates\; of uiui.\; Typical\; DFS\; (depth\; first\; search)\; algorithm\; is\; used\; here.}$

Suppose the current officer is $\mathrm{aa and\; he\; spreads\; a\; command.\; Officer aa chooses bb —\; one\; of\; his\; direct\; subordinates\; (i.e.\; a\; child\; in\; the\; tree)\; who\; has\; not\; received\; this\; command\; yet.\; If\; there\; are\; many\; such\; direct\; subordinates,\; then aa chooses\; the\; one\; having\; minimal\; index.\; Officer aa gives\; a\; command\; to\; officer bb.\; Afterwards, bb uses\; exactly\; the\; same\; algorithm\; to\; spread\; the\; command\; to\; its\; subtree.\; After bb finishes\; spreading\; the\; command,\; officer aa chooses\; the\; next\; direct\; subordinate\; again\; (using\; the\; same\; strategy).\; When\; officer aa cannot\; choose\; any\; direct\; subordinate\; who\; still\; hasn\text{'}t\; received\; this\; command,\; officer aa finishes\; spreading\; the\; command.}$

Let's look at the following example:

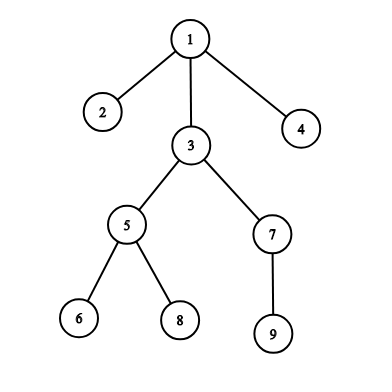
If officer $\mathrm{11 spreads\; a\; command,\; officers\; receive\; it\; in\; the\; following\; order: [1,2,3,5,6,8,7,9,4][1,2,3,5,6,8,7,9,4].}$

If officer $\mathrm{33 spreads\; a\; command,\; officers\; receive\; it\; in\; the\; following\; order: [3,5,6,8,7,9][3,5,6,8,7,9].}$

If officer $\mathrm{77 spreads\; a\; command,\; officers\; receive\; it\; in\; the\; following\; order: [7,9][7,9].}$

If officer $\mathrm{99 spreads\; a\; command,\; officers\; receive\; it\; in\; the\; following\; order: [9][9].}$

To answer the $\mathrm{ii-th\; query (ui,ki)(ui,ki),\; construct\; a\; sequence\; which\; describes\; the\; order\; in\; which\; officers\; will\; receive\; the\; command\; if\; the uiui-th\; officer\; spreads\; it.\; Return\; the kiki-th\; element\; of\; the\; constructed\; list\; or -1 if\; there\; are\; fewer\; than kiki elements\; in\; it.}$

You should process queries independently. A query doesn't affect the following queries.

Input

The first line of the input contains two integers $\mathrm{nn and qq (2\le n\le 2\cdot 105,1\le q\le 2\cdot 1052\le n\le 2\cdot 105,1\le q\le 2\cdot 105)\; —\; the\; number\; of\; officers\; in\; Berland\; army\; and\; the\; number\; of\; queries.}$

The second line of the input contains $\mathrm{n-1n-1 integers p2,p3,\dots ,pnp2,p3,\dots ,pn (1\le pi<i1\le pi<i),\; where pipi is\; the\; index\; of\; the\; direct\; superior\; of\; the\; officer\; having\; the\; index ii.\; The\; commander\; has\; index 11 and\; doesn\text{'}t\; have\; any\; superiors.}$

The next $\mathrm{qq lines\; describe\; the\; queries.\; The ii-th\; query\; is\; given\; as\; a\; pair\; (ui,kiui,ki)\; (1\le ui,ki\le n1\le ui,ki\le n),\; where uiui is\; the\; index\; of\; the\; officer\; which\; starts\; spreading\; a\; command,\; and kiki is\; the\; index\; of\; the\; required\; officer\; in\; the\; command\; spreading\; sequence.}$

Output

Print $\mathrm{qq numbers,\; where\; the ii-th\; number\; is\; the\; officer\; at\; the\; position kiki in\; the\; list\; which\; describes\; the\; order\; in\; which\; officers\; will\; receive\; the\; command\; if\; it\; starts\; spreading\; from\; officer uiui.\; Print\; "-1"\; if\; the\; number\; of\; officers\; which\; receive\; the\; command\; is\; less\; than kiki.}$

You should process queries independently. They do not affect each other.

Example

input

Copy

9 6
1 1 1 3 5 3 5 7
3 1
1 5
3 4
7 3
1 8
1 9

output

Copy

3
6
8
-1
9
4


求从u考试按深度遍历第k个数是多少，没有则为-1
1为根，从根遍历求的顺序储存，其它的点遍历一定在根遍历的子序列中，所以只要求下从u开始遍历有多少个，并且开始的位置再根遍历的序列中的第几位就行了。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5+10;
std::vector<int> v[N];
int n, q, x, ans = 1, tot;
int a[N], cnt[N];
map<int,int> mp;
void dfs(int u) {
    int tmp = ans;
    for(int i = 0; i < v[u].size(); i ++) {
        ans++;
        a[tot++] = v[u][i];
        dfs(v[u][i]);
    }
//    printf("%d %d %d
",u,ans,tmp );
    cnt[u] = ans - tmp+1;
}
int main() {
    cin >> n >> q;
    for(int i = 2; i <= n; i ++) {
        scanf("%d", &x);
        v[x].push_back(i);
    }
    a[tot++] = 1;
    cnt[1] = n;
    dfs(1);
    for(int i = 0; i < tot; i ++) {
        mp[a[i]] = i;
    }
    // for(int i = 1; i <= tot; i ++) printf("%d ", cnt[i]);printf("
");
    while(q--) {
        int u, x;
        scanf("%d%d",&u, &x);
        if(cnt[u] < x) printf("-1
");
        else {
            printf("%d
",a[mp[u]+x-1]);
        }
    }
    return 0;
}