树状数组的概念:
树状数组(Fenwick Tree,又称二叉索引树)是一个查询和修改复杂度都为log(n)的数据结构,它是利用二进制的一些特点来实现。它的功能有局限性,主要是用来动态查询连续和(或者是前缀和)的问题。它利用O(n)的附加空间复杂度,将线性的数列结构转化成树状结构从而进行跨越扫描,高效完成查询连续和。
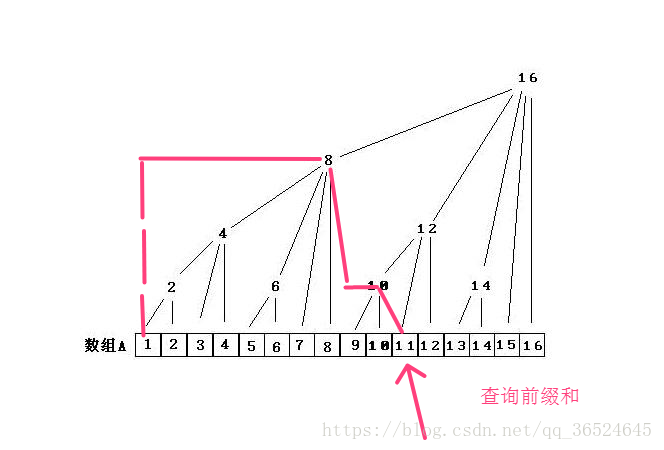
看图来推导一下他们的对应关系:
C2=A1+A2 C4=C2+A3+A4=A1+A2+A3+A4 C6=A5+A6.......
这里就不一一列出所有对应关系了,读者可以非常明白的看到是如何对应的。
经典例题与分析:
那么这里给出一例:给出一个n个元素的数组A1,A2,A3...An,要求对他们进行两种操作: 1、Add操作:Add(x,d)让Ax加上d。2、Query操作:Query(L,R)计算Al+A(l+1)+...+Ar。
这是一个很典型的动态查询区间和问题,如果按朴素前缀和递推的算法,那么每次修改一个参数后都要重新计算后面所有的前缀和数组S的值,修改m次值,每次递推重新计算前缀和数组S,时间复杂度为T(n)=O(m*n)(m为执行指令Add的次数),那么当m、n均大于10000时将无法承受时间复杂度,那么就要靠树状数组了!
在学习树状数组前,要先介绍一个新函数lowbit(x),他的作用是将x转换为二进制之后从右往左第一个1的位置。这个函数很重要,是建树的索引,那么如何实现这样一个函数呢?给出公式:lowbit ( x ) = x & ( -x )
为什么x&(-x)可以实现这个功能?在计算机中负号具体运算规则为:按位取反(包括首位表示符号的一位),末尾加1之后的结果,还是给读者举上一例:8转化为二进制:0 1000 取反:1 0111 加一:1 1000 转回十进制:(符号1为负数)-8。这是‘-’取反的意义,那么‘&‘意义是将两个数字二进制进行比较,相同位数字都为则为1,否则为0,那么最后他们取&,算出的不就是从右往左1最先出现的位置了么。这个函数介绍完了,就可进入正题了,请读者观察上图联系刚刚介绍的lowbit函数,有什么发现呢?无论是在叶子上,还是在中间的节点上,对于左子节点,它的父亲节点编号是i+lowbit(i),对于右子节点,它的父亲节点编号是i-lowbit(i),而且还有一个很重要的发现,那就是C数组的覆盖范围:C[x]的区间是[x-lowbit(x)+1,x],读者可以自行验算。
有了以上理论支持,问题便不难分析了,我要计算A1+A2+A3+...+A11,也就是A11的前缀和,如何计算?从11开始向左边走,用C对应的数组不重复也不漏地走到A1,所加起来的和便是所要的答案,具体可以见上图中红色标记,A11的前缀和=A11+C10+C8,明白了么?
有了计算的方法,那么修改一个叶子上的值会变化哪些值呢?只需同刚才使用的方法,将上面的根节点都加上d即可完成修改。也就是说修改的值就很少了,时间复杂度T(n)=O(logn)。
本题还有一个问题,非常简单,就是要求计算的是闭合区间[L,R]的和,而树状数组算出的却是前缀和,那如何才能转换过来呢?数学中学过的集合,用A表示Ar的前缀和,用B表示Al的前缀和,则B⊆A&&A!=B,那么[L,R]=A为全集的B的补集,用pre_sum(x)表示前缀和,则闭合区间[L,R]中元素的和为pre_sum[R]-pre_sum[L-1]。
接下来上代码:
#include <bits/stdc++.h> using namespace std; const int MAXN=500005; int C[MAXN],N,M,num; int lowbit(int v){return v&(-v);} void Add(int x,int value){ while(x<=N){ C[x]+=value; x+=lowbit(x); } return; } int pre_Query(int k){ int sum=0; while(k>0){ sum+=C[k];k-=lowbit(k); } return sum; } int pre_sum(int L,int R){ return pre_Query(R)-pre_Query(L-1); } int main(){ cin>>N>>M; for(int i=1;i<=N;i++){ cin>>num; Add(i,num); } for(int i=1;i<=M;i++){ int code,par1,par2; scanf("%d",&code); if(code==1){scanf("%d%d",&par1,&par2);Add(par1,par2);} if(code==2){ scanf("%d%d",&par1,&par2); printf("%d ",pre_sum(par1,par2)); } } return 0; }