这道题引入了一个新的概念:出租车几何,不过在题目中已经给出了他的定义,我们先来看一下这道题。
题目:19世纪的德国数学家赫尔曼·闵可夫斯基(Hermann Minkowski)研究了一种名为出租车几何学的非欧几何。 在出租车几何里T1(x1,y1) T2(x2,y2)两点之间的距离被定义为dis(T1,T2)=∣x1−x2∣+∣y1−y2∣(曼哈顿距离)。 其他定义均与欧几里得几何相同。例如圆的定义:在同一平面内,到定点(圆心)的距离等于定长(半径)的点的集合。
我们对欧几里得几何与出租车几何两种定义下半径为R的圆的面积很感兴趣。解决这个问题的重担就落在你身上了。
第一行输出欧几里得几何下半径为R的圆的面积,第二行输出出租车几何下半径为R的圆的面积。
注意:你的输出与标准答案绝对误差不超过0.0001将会被认为正确
这道题代码很简单,关键是如何去理解出租车几何中的圆。 首先我们来想想在欧几里得几何中圆的定义:
在同一平面内,到定点的距离等于定长的点的集合叫做圆。
不管在什么几何中,圆的定义是一样的,所以我们是要在平面直角坐标系中找到一个封闭图形使它上面任意一个点的横纵坐标之和等于R, 首先能明确的一点是在坐标轴上横纵坐标中总有一个为0,这点很关键任取一个R,可以在平面直角坐标系中先标出这四个点A,B,C,D,然后在OB上任意取一点F,过F做Y轴垂线EF,因为为了让OF+EF=OF+BF=OB,所以EF一定要等于BF,所以△BEF为等腰RT三角形,延长BE因为OA等于OB,所以∠ABO=∠EBF,A,E,B三点共线。于是可以证得E在○O上(出租车几何定义的圆),由此可以作出一整个圆,图形如下:
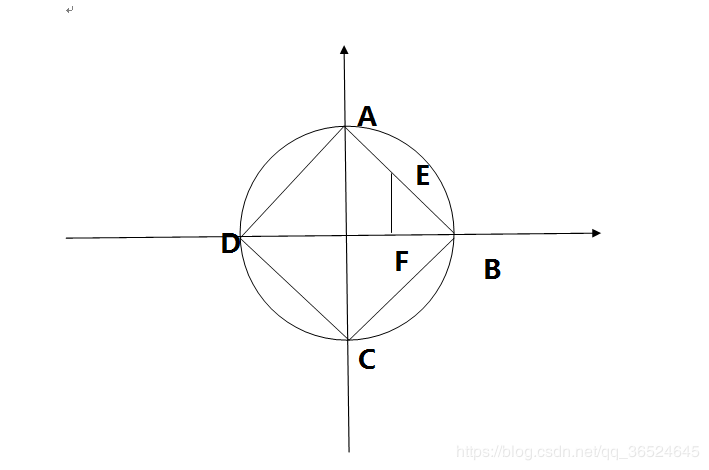
发现是一个正方形!既然如此,他的面积就等于R*R*2,这就不必多说了,那么代码实现很简单,无非就是把π的精度思考一下,包括输入输出的格式控制好就完事了,代码如下:
#include <bits/stdc++.h> using namespace std; double p=3.1415926535898; int main(){ double r; scanf("%lf",&r); printf("%.6lf %.6lf",r*r*p,r*r*2); return 0; }