二叉排序树的删除操作

算法思想

二叉排序树，删除操作主要针对三种情况。

1 叶子节点-直接删除就可以了

2 没有左孩子的节点-直接嫁接右子树就可以了(没有右孩子的节点-直接嫁接左子树就可以了)

3 如果左右子树都存在，则寻找删除节点的直接前驱（即左子树里面的最右的节点）

编程时需要注意，函数时针对指针的操作，因此为了修改指针，要使用二级指针传参才可以

例如：

void delete(BinaryTree **b){

　　....

}

int main(){

　　BinaryTree *b = (BinaryTree *)malloc(sizeof(BinaryTree));

　　delete(&b);

}

函数代码：

bool deleteTree(BTree **b,int key){
    if(!*b)
        return false;
    else{
        if((*b)->data == key){
            return deleteNode(&(*b));
        }
        else if((*b)->data > key)
            return deleteTree(&(*b)->lchild,key);
        else
            return deleteTree(&(*b)->rchild,key);
    }
}
bool deleteNode(BTree **b){
    BTree *p,*s;
    if((*b)->lchild == NULL ){
        p = (*b);
        (*b) = (*b)->rchild;
        free(p);
    }else if((*b)->rchild == NULL){
        p = (*b);
        (*b) = (*b)->lchild;
        free(p);
    }else{
        p = (*b);
        s = (*b)->lchild;
        while(s->rchild != NULL){
            p = s;
            s = s->rchild;
        }
        (*b)->data = s->data;
        if(p != (*b))
            p->rchild = s->lchild;
        else
            p->lchild = s->lchild;
        free(s);
        return true;
    }
}

全部代码：

  1 #include <stdio.h>
  2 #include <stdlib.h>
  3 typedef struct bTree{
  4     int data;
  5     struct bTree *lchild,*rchild;
  6 }BTree;
  7 
  8 void initialTree(BTree *b);
  9 bool insertTree(BTree *b,int key);
 10 int searchTree(BTree *b,int key,BTree *f,BTree *&p);
 11 void InOrderTree(BTree *b);
 12 bool deleteTree(BTree **b,int key);
 13 bool deleteNode(BTree **b);
 14 
 15 int main(){
 16     BTree *b = (BTree *)malloc(sizeof(BTree));
 17     b->data = 5;
 18     b->lchild = b->rchild = NULL;
 19     initialTree(b);
 20     InOrderTree(b);
 21     deleteTree(&b,4);
 22     InOrderTree(b);
 23     getchar();
 24     return 0;
 25 }
 26 bool deleteTree(BTree **b,int key){
 27     if(!*b)
 28         return false;
 29     else{
 30         if((*b)->data == key){
 31             return deleteNode(&(*b));
 32         }
 33         else if((*b)->data > key)
 34             return deleteTree(&(*b)->lchild,key);
 35         else
 36             return deleteTree(&(*b)->rchild,key);
 37     }
 38 }
 39 bool deleteNode(BTree **b){
 40     BTree *p,*s;
 41     if((*b)->lchild == NULL ){
 42         p = (*b);
 43         (*b) = (*b)->rchild;
 44         free(p);
 45     }else if((*b)->rchild == NULL){
 46         p = (*b);
 47         (*b) = (*b)->lchild;
 48         free(p);
 49     }else{
 50         p = (*b);
 51         s = (*b)->lchild;
 52         while(s->rchild != NULL){
 53             p = s;
 54             s = s->rchild;
 55         }
 56         (*b)->data = s->data;
 57         if(p != (*b))
 58             p->rchild = s->lchild;
 59         else
 60             p->lchild = s->lchild;
 61         free(s);
 62         return true;
 63     }
 64 }
 65 void InOrderTree(BTree *b){
 66     if( !b )
 67         return;
 68     InOrderTree(b->lchild);
 69     printf("%d ",b->data);
 70     InOrderTree(b->rchild);
 71 }
 72 
 73 void initialTree(BTree *b){
 74     insertTree(b,5);
 75     insertTree(b,3);
 76     insertTree(b,4);
 77     insertTree(b,6);
 78     insertTree(b,2);
 79     insertTree(b,1);
 80     insertTree(b,8);
 81 }
 82 int searchTree(BTree *b,int key,BTree *f,BTree *&p){
 83     if(!b){
 84         p = f;
 85         printf("++%d
",p->data);
 86         return 0;
 87     }
 88     else if( key == b->data){
 89         p = b;
 90         printf("--%d 
",p->data);
 91         printf("找到元素key:%d
",key);
 92         return 1;
 93     }
 94     else if(key > b->data)
 95         return searchTree(b->rchild,key,b,p);
 96     else
 97         return searchTree(b->lchild,key,b,p);
 98 }
 99 bool insertTree(BTree *b,int key){
100     BTree *p,*s;
101     if(!searchTree(b,key,NULL,p)){
102         printf("%d 没有出现在树中，可以插入在%d之后
",key,p->data);
103         s = (BTree *)malloc(sizeof(BTree));
104         s->data = key;
105         s->lchild = s->rchild = NULL;
106         if(!b){
107             b = s;
108         }
109         else if(key < p->data){
110             p->lchild = s;
111         }else{ 
112             p->rchild = s;
113         }
114         return true;
115     }else
116         return false;
117 }

View Code

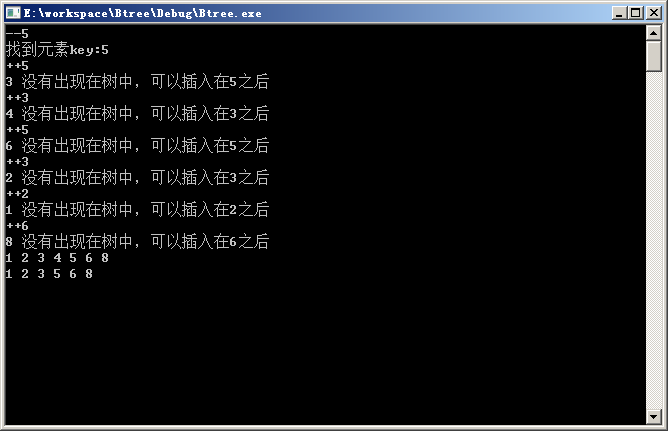
运行示例：

相关阅读:
c++ struct 使用
 c++数组、字符串操作
 c++ List、Vector、Stack、Queue使用
 十三、哈希表
 十二、234树
 十一、红黑树
 十、哈夫曼编码
 九、二叉树
 八、高级排序
 七、递归
原文地址：https://www.cnblogs.com/xing901022/p/3654333.html