一、时间序列定义
时间序列也成动态序列,是指将某种现象的指标数值按照时间顺序排列而成的数值序列。时间序列有两个组成要素构成:1、第一个要素是时间要素;2、第二个是数值要素。时间序列根据时间和数值性质的不同 ,可以分为时期时间序列和时点时间序列。
二、时间序列分解
时间序列数值变化背后必然蕴含着数值变换的规律性,一般情况下 ,时间序列的数值变化规律有以下四中:长期变动趋势、季节变动规律、周期变动规律和不规则变动。根据影响因素对时间序列数值变化趋势的不同影响情况,可以分为四中影响因素:长期趋势影响因素、季节变动影响因素、循环变动影响因素和不规则变动影响因素。
1、长期趋势
长期趋势指的是统计指标在相当长的一段时间内,受到长期趋势影响因素的影响,变现出持续上升或持续下降的趋势,通常用字母T表示。
2、季节变动
季节变动是指由于季节的转变使得指标数值发生周期性变动。指标数值的季节变动是以年为周期的,一般以月、季、周为时间单位,不能以年做单位,通常用S表示。有自然因素也有人为因素。
3、循环变动
循环变动与季节变动的周期不同,循环变动通常以若干年为周期,在曲线图上变现为波浪式的周期变动。这种周期变动的特征表现为增加和减少交替出现。最典型的周期案例就是市场经济的商业周期。
4、不规则变动
不规则变动是由某些随机因素导致的数值变化,这些因素的作用是不可预知和没有规律的,因此对数值的变化影响变形为不规则变动。
以上四种变动就是时间序列数值变化的分解结果。有时这些变动会同时出现在一个时间序列里面 ,有时也可能只出现一种或几种,这是由引起各种变动的影响因素决定的。四种变动与指标数值最终变动的关系可能是叠加关系,也可能是乘积关系。
叠加模型:如果四种变动之间是相互独立的关系,那么叠加模型可以表示为:
Y=T+S+C+I
Y表示指标数值的最终变动;
T表示长期趋势变动;
S表示季节变动;
C表示循环变动;
I表示不规则变动;
乘积模型:如果四种变动之间存在相互影响关系,那么应该使用乘积模型:
Y=T*S*C*I
反映在具体的时间序列图上,如果随着时间的推移,序列的季节波动边的越来越大,则反映各种变动之间的关系发生变化,建议使用乘积模型;反之,如果时间序列图的波动保持恒定,则可以之间使用叠加模型。
三、时间序列分析及分类
时间序列分析分为两种形式:1、传统的时间序列分析方法,研究时间序列是否能被分解成上面介绍的四种变动 ,并解析引起每种变动的影响因素。2、时间序列的模型解析法,常用时间序列模型有自回归(AR)模型、滑动平均(MA)模型、自回归滑动平均(ARMA)模型等。
根据平稳性的不同没时间序列可以分为平稳性时间序列和非平稳性时间序列
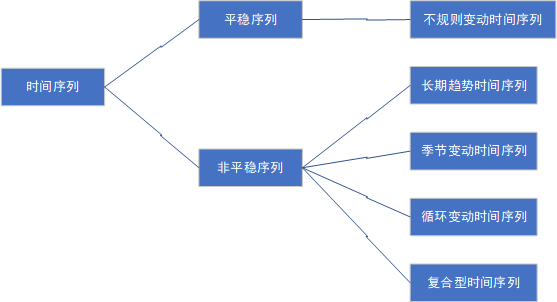
四、时间序列分析法
因为传统时间序列分析技术(时间序列分解法)的缺陷,所以统计学家开发出更为通用的时间序列分析方法,其中AR/MR/ARMR/ARIMA在这个发展过程中扮演课非常重要的角色,知道现在,他们都在实际工作生活发挥重要作用。这四种分析方法的共同特点都是跳出变动成分的分析角度,从时间序列本身出发,力求得出前期数据与后期数据的量化关系,从而建立前期数据为自变量,后期数据为因变量的模型,达到预测的目的。
AR/MR/ARMR/ARIMR是四种可以独立使用的分析方法,是互补的关系,适用于包含不同变动成分的时间序列。AR/MR/ARMA用于分析平稳时间序列,ARIMA通过差分可以用于处理非平稳时间序列。一般具有长期趋势的时间序列都是非平稳时间序列。根据趋势的不同,可以使用差分将具有长期趋势的时间序列转换成平稳时间序列。例如,线性增长的长期趋势,可以通过一阶差分形成新的平稳的时间序列。例如时间序列的数值为线性增长的(1,2,3,4,5,6,7,8),经过一阶差分以后,新的时间序列的数值为(1,1,1,1,1,1,1),就成为稳定的时间序列了。
根据长期趋势的发展趋势不同,可以进行差分的次数和方法也不相同,一般的规律如下:
1、一次差分的时间序列数值大体相同,配合直线趋势
2、二次差分的时间序列数值大体相同,配合二次曲线
3、对数的一次差分的时间序列数值大体相同,配合指数曲线
4、一次差分的环比值大体相同 ,配合修正指数曲线
5、对数一次差分的环比值大体相同,配合Gompertz曲线
6、倒数一次差分的环比值大体相同,配合Logistic曲线
五、AR/MA/ARMA模型
1、AR模型(auto regressive model)
如果某个时间序列的任意数值可以表示为下面的回归方程,那么该时间序列服从p阶的自回归过程,可以表示为AR(p):

可以发现,AR模型利用前期数值与后期数值的相关关系(自相关),建立包含前期数值和后期数值的回归方程,达到预测的目的,因此成为自回归过程。这里需要解释白噪声,大家可以将白噪声理解成时间序列数值的随机波动,这些随机波动的总和会等于0,例如前面统计基础文章中介绍的,某条饼干的自动化生产线,要求每包饼干为500克,但是生产出来的饼干产品由于随机因素的影响,不可能精确的等于500克,而是会在500克上下波动,这些波动的总和将会等于互相抵消等于0。
2、MA模型(moving average model)
如果某个时间序列的任意数值可以表示成下面的回归方程,那么该时间序列服从q阶的移动平均过程,可以表示为MA(q):

可以发现,某个时间点的指标数值等于白噪声序列的加权和,如果回归方程中,白噪声只有两项,那么该移动平均过程为2阶移动平均过程MA(2)。比较自回归过程和移动平均过程可知,移动平均过程其实可以作为自回归过程的补充,解决自回归方差中白噪声的求解问题,两者的组合就成为自回归移动平均过程,称为ARMA模型。
3、ARMA模型(auto regressive and moving average model)
自回归移动平均模型由两部分组成:自回归部分和移动平均部分,因此包含两个阶数,可以表示为ARMA(p,q),p是自回归阶数,q为移动平均阶数,回归方程表示为:
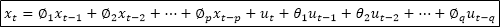
从回归方程可知,自回归移动平均模型综合了AR和MA两个模型的优势,在ARMA模型中,自回归过程负责量化当前数据与前期数据之间的关系,移动平均过程负责解决随机变动项的求解问题,因此,该模型更为有效和常用。
4、ARIMA 差分自回归移动平均模型
ARIMA模型能够用于齐次非平稳时间序列的分析,这里的齐次指的是原本不平稳的时间序列经过d次差分后成为平稳时间序列。差分自回归移动平均模型写成ARIMA(p,d,q)。p代表自回归阶数;d代表差分次数;q代表移动平均阶数。在spss软件中,有时输出的ARIMA模型包括6个参数:ARIMA(p,d,q)(P,D,Q),这是因为如果时间序列中包含季节变动成分的话,需要首先将季节变动分解出来,然后再分别分析移除季节变动后的时间序列和季节变动本身。这里小写的p,d,q描述的是移除季节变动成分后的时间序列;大写的P,D,Q描述的是季节变动成分。两个部分是相乘的关系。因此,ARIMA(p,d,q)(P,D,Q)也被称为复合季节模型。
总结
以上介绍了两个时间序列分析的体系:时间序列分解模型体系和AR/MA/ARMA/ARIMA模型体系。两者的分析原理是不同的,时间序列分解是力求将时间序列分解成不同的变动成分,分析每种变动成分的规律,然后在综合各种成分的规律用于预测;AR/MA/ARMA/ARIMA模型体系是从时间序列数值本身的相关关系出发,将移动平均技术、相关分析技术和平稳技术(差分)等纳入模型,力求建立时间序列数值之间的回归方程,从而达到预测的目的。