堆排序与快速排序,归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法。堆排序是跟二叉堆联系在一起的,它是利用二叉堆的性质设计的一种算法。所以它有父节点值总是大于(或小于其所有子节点)。一般情况下,二叉堆是如下所示的:
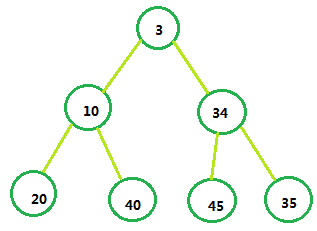 这是一个正序从小到大的序列。
这是一个正序从小到大的序列。
首先,肯定是插入问题了,我们首先要构造好一个堆。其实这里的插入用插入排序的方法就可以了。他的实现就是直接插入。。
1 void minHeapFixUp(int *arrayL, int newElementIndex) { 2 int fatherIndex = (newElementIndex - 1) / 2; 3 int temp = arrayL[newElementIndex]; 4 5 //当新加入的子节点的值小于父节点的时候,将其变为父节点... 6 //同时向上遍历找到最终的某个元素出现其父元素值大于这个新加入 7 //节点的时候停止 8 while (fatherIndex >= 0 && newElementIndex != 0) { 9 if (arrayL[fatherIndex] < temp) 10 break; 11 12 arrayL[newElementIndex] = arrayL[fatherIndex]; 13 newElementIndex = fatherIndex; 14 fatherIndex = (newElementIndex - 1) / 2; 15 } 16 arrayL[newElementIndex] = temp; 17 } 18 19 void insertElement(int* arrayL, int insertIndex, int value) { 20 arrayL[insertIndex] = value; 21 minHeapFixUp(arrayL, insertIndex); 22 }
二叉堆的堆化:什么叫二叉堆的堆化?也就是讲一个序列变成一个符合二叉堆的样子的序列,也就是从父节点要比所有子节点小(或大)。比如:
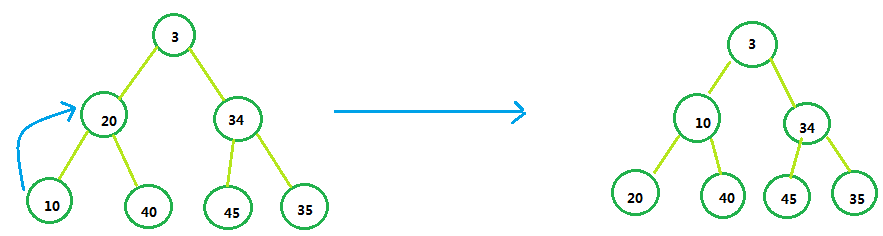
那应该如何用程序对一个序列进行堆化呢【一般情况下我们用数组储存元素】,首先我们要知道一点,父节点和子节点的下标的关系是:
fatherNode = (sonNode - 1) / 2;
sonNode1 = 2 * father + 1;
sonNode2 = 2 * fatherNode + 2;
有了这三条,我们就可以根据节点来对其子节点或父节点进行处理了。
下面我们来谈谈堆化数组:
堆化数组,就是将一个数组变成符合二叉堆性质的数组。那么要如何进行堆化呢,我们可以先将未堆化的数组看成一个二叉树。首先我们从树叶A开始将其与其父节点B变得有序,然后处理其父节点B与B的父节点...如此下去就可以将整个树变成二叉堆。
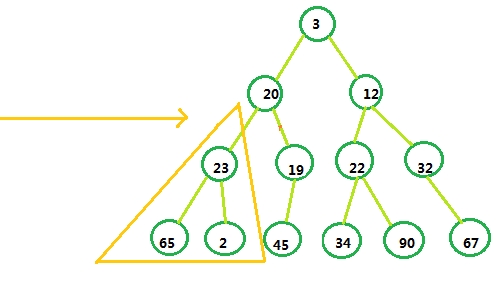
我们来看个例子:对数组 Array[3, 20, 12, 23, 45, 22, 32, 65, 2, 19, 34, 90, 67],用图表示如下:
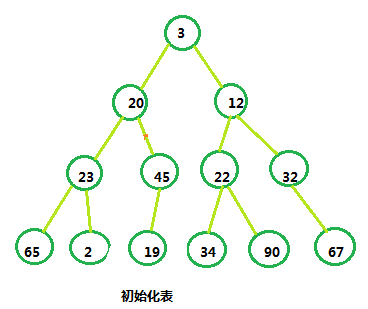
我们可以看出,有第二,第三个叶节点不满足堆的要求,而其他的在父节点和子节点之间已经满足对的条件。所以我们首先将Array[5]和Array[10]互换。Array[4]和Array[9]同理。
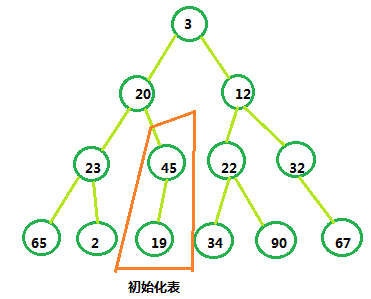

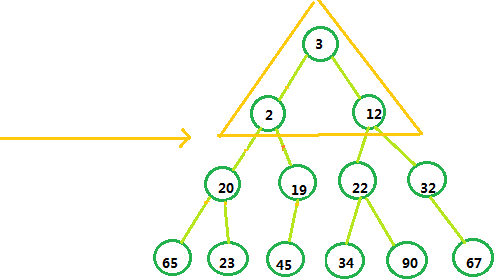
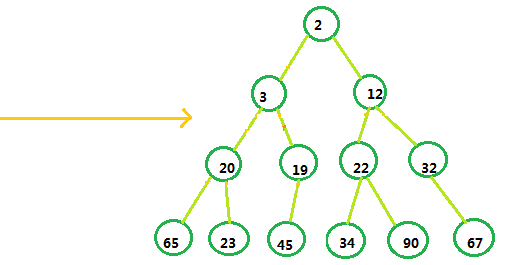 至此,堆化完毕,我们可以看到,这已经是一个有效的二叉堆了。
至此,堆化完毕,我们可以看到,这已经是一个有效的二叉堆了。
那么,我们改怎样用代码来实现呢?如下:
1 void minHeapFixDown(int *arrayL, int beginIndex, int totalNode) { 2 int temp = arrayL[beginIndex]; 3 int sonNode = beginIndex * 2 + 1; 4 5 while (sonNode < totalNode) { 6 //找到最小那个子节点(如果是两个的话) 7 if (sonNode + 1 < totalNode && arrayL[sonNode] > arrayL[sonNode + 1]) 8 sonNode++; 9 10 if (arrayL[sonNode] >= temp) 11 break; 12 13 a[beginIndex] = arrayL[sonNode]; 14 //向上遍历 15 beginIndex = sonNode; 16 sonNode = beginIndex * 2 + 1; 17 } 18 arrayL[beginIndex] = temp; 19 } 20 21 void makeMinHeap(int *arrayL, int len) { 22 //遍历每一个子节点,并与父节点比较,进行处理 23 for (int i = len / 2 - 1; i >= 0; i--) 24 minHeapFixDown(arrayL, i, len); 25 }
下面来看看怎么删除元素:在二叉堆中,我们删除元素都是讲Array[0]删除然后将最后一个元素补上。然后再进行一次堆化。那么就是如下:
1 void deleteNode(int* arrayL, int len) { 2 swap(arrayL[0], arrayL[len - 1]); 3 minHeapFixDown(arrayL, 0, len - 1); 4 }
我们直接将Array[0]交换到数组最后,原因下面再说明。
到这里,我们就可以进行排序了。其实堆排的原理就是将第一个节点取出,然后再堆化数组,然后再取出新数组的第一个元素,接到原来取出的那个后面。因为第一个元素总是整个数组中最小的一个,所以取出来的数就是一个有序列了。
1 void heapSort(int *arrayL, int len) { 2 makeMinHeap(arrayL, len); 3 4 for (int i = len - 1; i >= 0; i--) { 5 swap(arrayL[0], arrayL[i]) 6 minHeapFixDown(arrayL, 0, i); 7 } 8 }
我们直接将新取出的元素接在数组后面,就可以用节省空间。。