求最大子数组

一.设计思想：

　　通过一个for循环。数组分别从0-最大，1-最大-0 等等依次 到最大-最大-1，通过这样的方式达到循环数组的目的。然后在每一个的数字里面，从第一个数开始向后按顺序相加，当相加结果为负数的时候，则此时不满足构成最大子数组的条件，然后从导致数组为负数的数的下一个数开始向后相加。最后求得此情况下的最大子数组和。然后分别求出N个最大子数组的和，然后在进行比较大小，得出最终的最大子数组的和。

二.出现的问题：

　　起初并没有实现在一个首尾相接的数组中，最大子数组和为正确值，例如 1 -2 -3 6 5 正确结果为12 最后得出结果为11。

三.问题的解决

　  通过大for循环里面嵌套小循环，来实现的数组的循环问题。然后在每个小循环里面求出最大的子数组和。最后再比较大小来求出最大子数组的和。

四.源代码：

package maxs;
import java.util.*;
public class maxs {
    public static void main(String[] args){
        Scanner sc=new Scanner(System.in); 
        int num;
        System.out.println("请输入数组长度");
        num=sc.nextInt();
        int zif[]=new int[num];//分别的数组
        int neir[]=new int[num]; //数组里面的数
        int sum1[]=new int[num]; //最大值
        int d=sum1[0];
        System.out.println("请输入数组内容：");
        for(int i=0;i<num;i++)//输入num个数
        {
            neir[i]=sc.nextInt();
        }       
         for(int j=0;j<num;j++)   
        {
            for(int k=0;k<num;k++)   //分别从0-num 1-num-0 .....
            {
                zif[k]=neir[(j+k)%num];
            }
            int sum=zif[0];//记录数组和
            int b=0;//进行记录
        
            for(int i=0;i<num;i++)
            {
                if(b<0)
                {
                    b=zif[i]; //b<0,b为加为负数那位的后一位
                }
                else
                {
                    b+=zif[i];
                }
                if(sum<b)
                {
                    sum=b; //sum为当前最大子数组的和
                }
                sum1[j]=sum;
            }
            if(d<sum1[j])
            {
                d=sum1[j]; //得到最终的最大和
            }
        }
        System.out.print("最大子数组和为：");
        System.out.print(d);
    }
}

五.结果截图：

　　

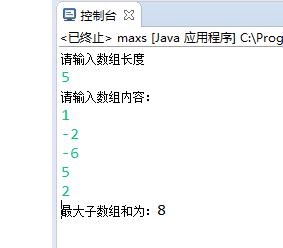
六.总结：

　　一个首尾相接的循环数组，可以在不同的位置起始。一个循环的数组可以分为从不同的位置开始。然后从第一个数，到最后一个数，每个数都当一次开始然后依次下去到结束。这样的N个数组凑起来就是一个首尾相接的循环数组。子数组的最大和则可以让开始的数开始向后面相加，当遇到结果为负数的时候，就不在满足条件了。应该从加的最后一个数的下一个数再开始进行相加。

　　我的收获的就是：起初自己并没有思路，不知道怎么来实现他。然后想想老师说的剪断，那么不就是分别在第一个数后， 第二个数后，，，依次来当作断点吗？将复杂问题，分解，让问题明白了许多。