A:
题意:给你一本书共c页,第一天看v0页,第二天看v0+a,第二天看v0+2a以此类推,每天最多看v1页,但是后一天要重复看前一天的后l页。
代码:
#include<stdio.h>
using namespace std;
int c,v0,v1,a,l;
int main()
{
while(~scanf("%d%d%d%d%d",&c,&v0,&v1,&a,&l))
{
int sum=v0;
int k=1;
while(sum<c)
{
sum-=l;
int cc=v0+k*a;
if(cc>v1)
cc=v1;
sum+=cc;
k++;
}
printf("%d
",k);
}
return 0;
}
B:
题意:
题意是给你一个正n边形,正多边形每两个顶点连成线。给你一个角度a,问哪三个顶点构成的角度最接近a,输出这个三个顶点的序号。
思路:每个顶点处内角度数:(n-2)*180/n。若n为偶数的时候,那一顶点处被划分的几个小角度数为((180-t)/2)相同的;若n为奇数,那顶点处被划分的角度数为(t-(n/2-1)*(180-t)),除了中间那个角以外的角度是相同的度数为((180-t)/2)。为什么是这样的?画图见分晓!
这题只要输出的适合解就可以了,所以你可以固定前两个顶点为1,2,去找合适的第三个顶点。
代码:
#include<stdio.h>
#include<algorithm>
#define Inf 1<<29
using namespace std;
int n;
double a,z;
int main()
{
while(~scanf("%d%lf",&n,&a))
{
double t=(n-2)*180.0/n;
double x=Inf;
int y=0;
double c=(180-t)/2;
double cc=t-(n/2-1)*2*c;
for(int i=1; i<=n-2; i++)
{
if(t>a)
z=t-a;
else
z=a-t;
if(z<x)
{
x=z;
y=i+2;
}
if(n%2==1&&i==n/2)
t-=cc;
else
t-=c;
}
printf("1 2 %d
",y);
}
return 0;
}
D:
题意:就是给你一个序列p[1]~p[n],每次把这个序列的最后一个数放在最前面,这样依次寻找最小的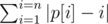 ,并输出。
,并输出。
思路:需要一个数组来动态记录a[i]-i<=0的个数,p[i]就表示移动i个位置后有多少个a[i]-i<=0。
代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define ll long long
const int maxn=1000010;
using namespace std;
int n;
int a[maxn];
int b[maxn];
int main()
{
while(~scanf("%d",&n))
{
ll sum=0;
memset(b,0,sizeof(b));
for(int i=1; i<=n; i++)
{
scanf("%d",&a[i]);
sum+=abs(a[i]-i);
if(a[i]-i<=0)
b[0]++;
else
b[a[i]-i]++;//因为若t=a[i]-i,往后移动序号每次增加1,那么至少需要移动t次才使得a[i]-i<=0
}
ll ans=sum;
ll cnt=b[0];//一开始是移动0次
int tt=0;
for(int i=1; i<n; i++)
{
int t=n-i+1;
if(a[t]-n<=0)//表示最后一个需要移动到最前的点,如果这个点对应的a[i]-i是负数,cnt--,因为你要找前面的,cnt表示的是所有的
cnt--;
if(a[t]-t<=0)//最后一个需要移动到最前的点,状态应该还原,就是原加了的就减去
b[0]--;
else
b[a[t]-t]--;
b[min(a[t]+i-1,maxn-10)]++;//最后一个需要移动到最前的点,移动之后造成的影响要更新,当前这个点已经移动了i个位置,但是从最后移动到最前差值为a[t]-1需要移动a[t]-1个位置才使得a[i]-i==0,则共需要移动a[t]-1+i个位置,那么p[a[n]-1+i]对应的值加一
sum+=cnt;//加上前面a[i]-i<=0的数往后移一位的变化值
sum-=(n-cnt-1);//减去前面a[i]-i>0的数往后移一位的变化值
sum-=abs(a[t]-n);//减去移动前最后一个点对应abs(a[i]-i)
sum+=abs(a[t]-1);//加上移动后第一个点对应的abs(a[i]-i)
cnt+=b[i];
if(sum<ans)
{
ans=sum;
tt=i;
}
}
printf("%lld %d
",ans,tt);
}
return 0;
}