题目大意:给你n个碗,求如何堆叠,使得它们的总高度最低。
首先,我们枚举碗的叠放顺序。
假设我们已经堆好了前i个碗,那么在堆第i+1个碗时,我们要将第i+1个碗与前i个碗比较,确定第i+1个碗的离地高度。
对于第i个碗和第j个碗的比较,我们分五种情况讨论(以下画图只画半个碗):
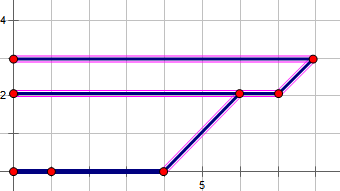 |
上方的碗底比下方的碗顶大,直接放上去即可 |
|
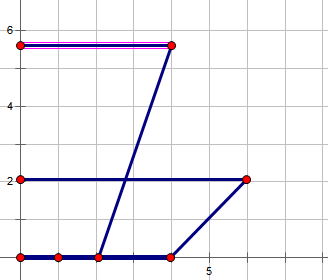
上方的碗底比下方碗底小,直接放上去即可 |
|
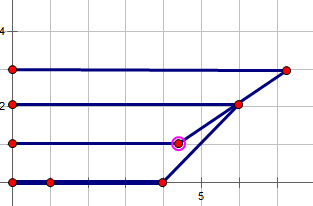
上方的碗边缘斜率小于下方的碗,且上方的碗比下方的碗大,的计算出其中一个碗的斜率,然后卡位即可 |
|
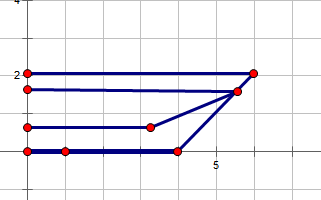
情况和上图类似,也是直接卡位即可。 |
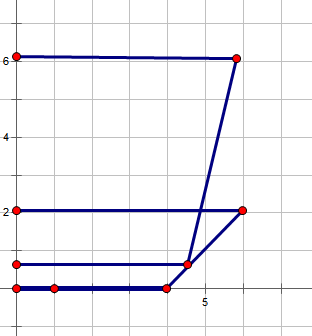
|
上方的碗边缘斜率大于下方的碗,也是直接卡位。 |
具体的细节可以看我的代码。
然后请一定要仔细检查所有细节(我错了一个字母调了2h)
1 #include<bits/stdc++.h> 2 #define M 10 3 using namespace std; 4 5 struct node{ 6 double a,b,c,d; 7 node(){a=b=c=d=0;} 8 node(double aa,double bb,double cc,double dd){ 9 a=aa; b=bb; c=cc; d=dd; 10 } 11 double xl(){return (d-b)/(c-a);} 12 friend double operator -(node a,node b){ 13 double p=a.b; a.b-=p; a.d-=p; 14 //if(a.a>=b.a&&a.c>=b.c) return p; 15 if(a.c<=b.a) return p+a.d; 16 if(a.xl()>b.xl()){ 17 if(b.c>=a.c){ 18 double k=a.d-(a.c-b.a)*b.xl(); 19 k=max(k,0.); 20 return p+k; 21 } 22 double k=a.d-b.d-(a.c-b.c)*a.xl(); 23 k=max(k,0.); 24 return p+k; 25 }else{ 26 if(b.a<=a.a) return p; 27 double k=a.d-(a.c-b.a)*a.xl(); 28 k=max(k,0.); 29 return p+k; 30 } 31 } 32 }a[M],s[M]; 33 int n,p[M]={0}; 34 int main(){ 35 scanf("%d",&n); 36 for(int i=1;i<=n;i++){ 37 double x,y,z; cin>>x>>y>>z; 38 a[i]=node(y,0,z,x); 39 } 40 for(int i=1;i<=n;i++) p[i]=i; 41 double minn=1e10; 42 while(1){ 43 memset(s,0,sizeof(s)); 44 s[0]=node(1e20,0,1e21,0); 45 for(int i=1;i<=n;i++){ 46 double maxn=0; 47 for(int j=0;j<i;j++) 48 maxn=max(maxn,s[j]-a[p[i]]); 49 s[i]=node(a[p[i]].a,maxn,a[p[i]].c,a[p[i]].d+maxn); 50 } 51 double maxn=0; 52 for(int i=1;i<=n;i++) maxn=max(maxn,s[i].d); 53 if(maxn<minn) 54 minn=min(minn,maxn); 55 if(!next_permutation(p+1,p+n+1)) break; 56 } 57 printf("%.0lf ",minn); 58 }