【xsy1232】Magic 最小割

题目大意：给你一个$n$个点，$m$条有向边的图，每个点有一个点权$a_i$，同时你可以用$b_i$的代价将$a_i$变为$0$

另外你要付出$sumlimits_{i=1}^nmaxlimits_{(i,j)}a_j$这么多代价。请最小化代价。

数据范围：$n≤1000$，$m≤50000$。

貌似是一道套路最小割

把每个点拆成两个点，对每条边新建一个点，将一个点的出边按终点的$a$从大到小排序后建图如下

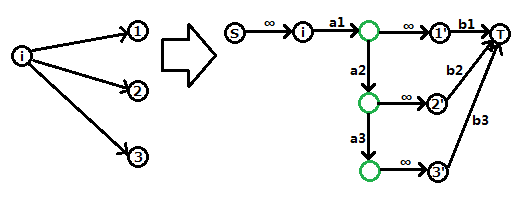
该建图方式，只有让某个前缀$a_i$全部变为$0$，一个点产生的费用才会改变，这个建图保证了如果要割$a_i$就必须要割掉$b_1$至$b_{i-1}$，且不会割掉两个$a$

我们对每个点都这么建一波，然后跑个最大流就没了

orzlyy！！！！！

#include<bits/stdc++.h>
#define M 60005
#define INF (1<<30)
using namespace std;

struct edge{int u,v,next;}e[M*4]={0}; int head[M]={0},use=0;
void add(int x,int y,int z){e[use].u=y;e[use].v=z;e[use].next=head[x];head[x]=use++;}
void Add(int x,int y,int z){add(x,y,z); add(y,x,0);}
int dis[M]={0},S,T; queue<int> q;
bool bfs(){
    memset(dis,0,sizeof(dis));
    dis[S]=1; q.push(S);
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(int i=head[u];~i;i=e[i].next)
        if(dis[e[i].u]==0&&e[i].v){
            dis[e[i].u]=dis[u]+1;
            q.push(e[i].u);
        }
    }
    return dis[T];
}
int dfs(int x,int flow){
    if(x==T) return flow; int sum=0;
    for(int i=head[x];~i;i=e[i].next)
    if(dis[x]+1==dis[e[i].u]&&e[i].v){
        int k=dfs(e[i].u,min(flow,e[i].v));
        sum+=k; flow-=k; 
        e[i].v-=k; e[i^1].v+=k;
        if(flow==0) return sum;
    }
    if(sum==0) dis[x]=-1;
    return sum;
}
int dinic(){
    int res=0;
    while(bfs()) 
    res+=dfs(S,INF);
    return res;
}

int n,m,a[M]={0},b[M]={0};
vector<int> g[M];
bool cmp(int x,int y){return a[x]>a[y];}
void ReadData(){
    memset(head,-1,sizeof(head));
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",a+i);
    for(int i=1;i<=n;i++) scanf("%d",b+i);
    for(int i=1;i<=m;i++){
        int x,y; scanf("%d%d",&x,&y);
        g[x].push_back(y);// g[y].push_back(x);
    }
}
void build(){
    S=0; T=2*n+1; int N=2*n+1;
    for(int i=1;i<=n;i++) Add(S,i,INF);
    for(int i=1;i<=n;i++) Add(i+n,T,b[i]);
    for(int x=1;x<=n;x++){
        sort(g[x].begin(),g[x].end(),cmp);
        for(int i=0;i<g[x].size();i++){
            N++;
            Add(i?N-1:x,N,a[g[x][i]]);
            Add(N,n+g[x][i],INF);
        }
    }
}
int main(){
    ReadData();
    build();
    cout<<dinic()<<endl;
}