二维数组求子数组和的最大值

          项目组成员：刘静（20092532），解凤娇（20112878），王洪叶（20112886）

          项目  名称：二维数组求子数组和的最大值

          项目  分析：对于一位数组求子数组的和的最大值，我们使用了穷举法，比较容易的得出了正确的结果，可是对于二维数组来说，难度确实是增加了，而且如果使用穷举法，就会使程序的复杂度大大增加。时间复杂度为O(n^5)。

 

 

#include<iostream>  #include<windows.h>
using namespace std; 
int sum1(int **PS,int imin,int imax,int j);
int Maxsum(int **PS,int **array,int m,int n)
{
    int Start,All;    
    int a,c; 
    int i,j;

    {  
        for (c=a;c<=n;c++)  
        {  
            Start=sum1(PS,a,c,m);  
            All=sum1(PS,a,c,m);  
            for (i=m-1;i>=1;i--)  
            {  
                if(Start>0)
                    Start+=sum1(PS,a,c,i);
                else
                    Start=sum1(PS,a,c,i);
                if(Start>All)
                    All=Start;
            }  
            if(All>MaxSum)
            {
                MaxSum=All;
            }
            
        }  
    }  
       cout<<"该二维数组的子数组的最大值为:"<<MaxSum<<endl;
    return 0;
}
int sum1(int **PS,int imin,int imax,int j)  
{  
    return PS[imax][j]-PS[imax][j-1]-PS[imin-1][j]+PS[imin-1][j-1];  
}  
int main()  
{
    int m,n;
    int i,j,k=1;
    int **PS;
    int **array;
    do{
        cout<<"请输入n行m列，以空格隔开：";  
        cin>>n>>m;
        cout<<endl;
        PS=(int **)malloc(sizeof(int*)*(n+1));  
        array=(int **)malloc(sizeof(int*)*(n+1));  
        for (i=0;i<=n;i++)  
        {  
            PS[i]=(int *)malloc(sizeof(int)*(m+1));  
            array[i]=(int *)malloc(sizeof(int)*(m+1));  
        }  
        cout<<"请输入"<<n<<"行"<<m<<"列数字："<<endl;  
        for (i=1;i<=n;i++)  
        {  
            for (j=1;j<=m;j++)  
            {  
                cin>>array[i][j];  
            }  
        }   
        Maxsum(& *PS,& *array,m,n);    
        system("pause");
        cout<<endl;
        cout<<"        1、继续"<<endl;
        cout<<"        0、退出"<<endl;
        cin>>k;
    }
    while(k!=0);
    return 0;    
} 

 

 

          进一步改进程序确实有点困难，是想到了使用二维变一维的方法，但是具体实施的时候，困难重重，所以参考了网上的部分代码，稍微有些初步的认识，首先是获取部分数组的和的数组。下面是我们的思路过程：

1 int sum1(int **PS,int imin,int imax,int j)  
2 {  
3     return PS[imax][j]-PS[imax][j-1]-PS[imin-1][j]+PS[imin-1][j-1];  
4 } 

//部分代码
for (i=0;i<=n;i++)  
    {  
        PS[i][0]=0;  
    }  
    for (j=0;j<=m;j++)  
    {  
        PS[0][j]=0;  
    }  
    for (i=1;i<=n;i++) //求部分数组的和 
    {  
        for (j=1;j<=m;j++)  
        {  
            PS[i][j]=array[i][j]+PS[i][j-1]+PS[i-1][j]-PS[i-1][j-1]; //表示以（0，0）为起点，以（i，j）为终点的连续子数组的和 
        }  
    }      

   最后通过循环遍历部分数组和的数组获取子数组的最大值。

#include<iostream>  
#include<windows.h>
using namespace std; 
int sum1(int **PS,int imin,int imax,int j);
int Maxsum(int **PS,int **array,int m,int n)
{
    int Start,All;    
    int a,c; 
    int i,j;
    int MaxSum=-1; 

    for (i=0;i<=n;i++)  
    {  
        PS[i][0]=0;  
    }  
    for (j=0;j<=m;j++)  
    {  
        PS[0][j]=0;  
    }  
    for (i=1;i<=n;i++) //求部分数组的和 
    {  
        for (j=1;j<=m;j++)  
        {  
            PS[i][j]=array[i][j]+PS[i][j-1]+PS[i-1][j]-PS[i-1][j-1]; //表示以（0，0）为起点，以（i，j）为终点的连续子数组的和 
        }  
    }      
    for (a=1;a<=n;a++) //枚举求子数组（转换为一维数组）最大值  
    {  
        for (c=a;c<=n;c++)  
        {  
            Start=sum1(PS,a,c,m);  
            All=sum1(PS,a,c,m);  
            for (i=m-1;i>=1;i--)  
            {  
                if(Start>0)
                    Start+=sum1(PS,a,c,i);
                else
                    Start=sum1(PS,a,c,i);
                if(Start>All)
                    All=Start;
            }  
            if(All>MaxSum)
            {
                MaxSum=All;
            }
            
        }  
    }  
       cout<<"该二维数组的子数组的最大值为:"<<MaxSum<<endl;
    return 0;
}
int sum1(int **PS,int imin,int imax,int j)  
{  
    return PS[imax][j]-PS[imax][j-1]-PS[imin-1][j]+PS[imin-1][j-1];  
}  
int main()  
{
    int m,n;
    int i,j,k=1;
    int **PS;
    int **array;
    do{
        cout<<"请输入n行m列，以空格隔开：";  
        cin>>n>>m;
        cout<<endl;
        PS=(int **)malloc(sizeof(int*)*(n+1));  
        array=(int **)malloc(sizeof(int*)*(n+1));  
        for (i=0;i<=n;i++)  
        {  
            PS[i]=(int *)malloc(sizeof(int)*(m+1));  
            array[i]=(int *)malloc(sizeof(int)*(m+1));  
        }  
        cout<<"请输入"<<n<<"行"<<m<<"列数字："<<endl;  
        for (i=1;i<=n;i++)  
        {  
            for (j=1;j<=m;j++)  
            {  
                cin>>array[i][j];  
            }  
        }   
        Maxsum(& *PS,& *array,m,n);    
        system("pause");
        cout<<endl;
        cout<<"        1、继续"<<endl;
        cout<<"        0、退出"<<endl;
        cin>>k;
    }while(k!=0);
    return 0;      
} 

 实验结果截图：

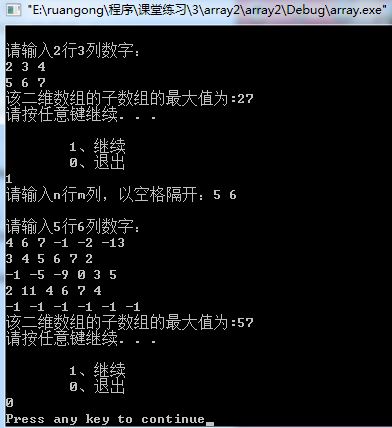
      实验心得：通过这几节小课的小实验，慢慢发现要想写好一个程序，真的很难，得考虑程序的规范、程序的时间复杂度、程序所能承受多大的考验

（程序测试），脚踏实地最靠谱，还需多加努力。