名词解释
树这个数据结构用到了递归的概念:树的子树还是树;
度:节点的子树个数;
树的度:树中任意节点的度的最大值;
兄弟:两节点的parent相同;
层:根在第一层,以此类推;
高度:叶子节点的高度为1,根节点高度最高;
有序树:树中各个节点是有次序的;
森林:多个树组成;
树的表示法
1.双亲表示法:每个节点存储:数据、parent在数组中的下标;
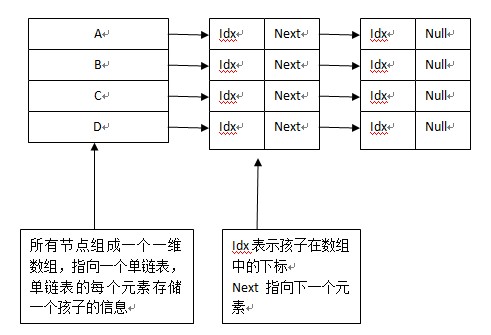
2.孩子表示法:全部节点组成一个数组,每个数组指向一个单链表,存放其孩子;如下图:
3.双亲孩子表示法

4.孩子兄弟表示法
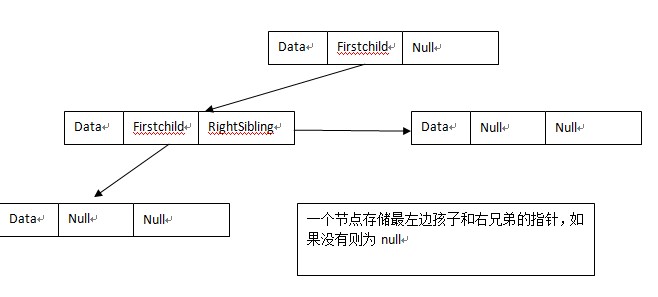
此种方法的好处在于一个多叉树能够转换成一颗二叉树,是树转换成二叉树的好办法;
线性表是树的特殊情况;
斜树:所有节点只有左节点或右节点;比如:
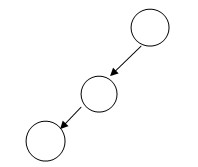
满二叉树:叶子节点一定要在最后一层,并且所有非叶子节点都存在左孩子和右孩子;
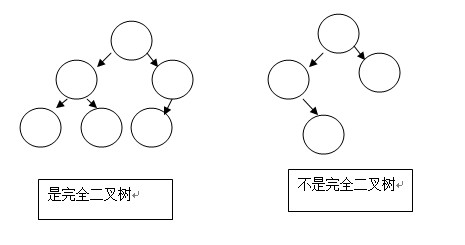
完全二叉树:从左到右、从上到下构建的二叉树;比如:
性质
1.第i层至多有个节点;
2.深度为k的树最多有2^k -1个节点;
3.任意二叉树,度为0的节点数=度为2的节点数+1;
4.如果i为父亲的编号,则孩子的编号为2i和2i+1;
5.如果孩子的编号为k,则父亲的编号为floor(k/2);
二叉树的存储结构
(1)顺序存储:只适用于完全二叉树;

(2)链式存储:最通用的存储方法;

但是这样很浪费空间,因为会有很多空指针(如果有n个节点,则有2n个left、right指针,但是用到的只有n-1个指针)
改进:线索二叉树:将空指针链接到前驱或后继节点;(此处前驱和后继是按照中序遍历上讲的)
节点数据结构如下图:
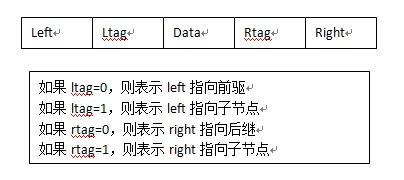
比如:
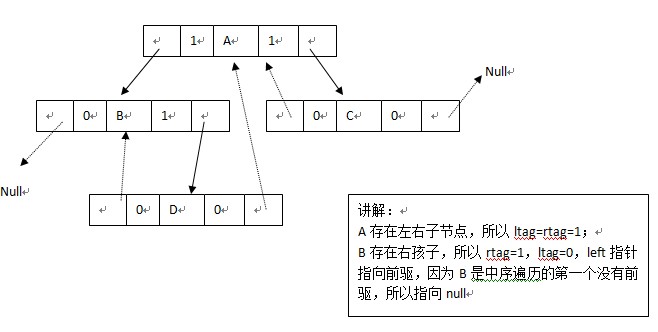
一般构造线索二叉树的过程步骤如下:
(1)构造一般二叉树;
(2)遍历二叉树的同时,建立线索二叉树;
二叉树的遍历
(1)前序遍历:先双亲、再左孩子、最后右孩子;
(2)中序遍历:先左孩子、再双亲、最后右孩子;
(3)后序遍历:先左孩子、再右孩子、最后双亲;
(4)层次遍历:一层一层,从左到右、从上到下遍历;
注意:
(1)已知前序、后序遍历结果,不能推导出一棵确定的树;
(2)已知前序、中序遍历结果,能够推导出后序遍历结果;
(2)已知后序、中序遍历结果,能够推导出前序遍历结果;
扩展二叉树
对于一般二叉树的扩充,为了能够通过一个遍历序列建立二叉树,扩展二叉树如图所示:

如果存在遍历序列:AB##C##,则可以很容易的建立二叉树;
此种方式很方便,因为一般来说都需要三种遍历方式中的两种才可以确定一个二叉树;
树、森林、二叉树的转换
树-->二叉树
根据兄弟孩子表示法进行转换;

森林-->二叉树

二叉树-->树

二叉树-->森林

Huffman编码
Huffman是一种前缀编码;
Huffman编码是建立在Huffman树的基础上进行的,因此为了进行Huffman编码,必须先构建Huffman树;
树的路径长度是每个叶节点到根节点的路径之和;
带权路径长度是(每个叶节点的路径长度*wi)之和;
Huffman树是最小带权路径长度的二叉树;
构造Huffman树的过程:
(1)将各个节点按照权重从小到大排序;
(2)去最小权重的两个节点,并新建一个父节点作为这两个节点的双亲,双亲节点的权重为子节点权重之和,再将此父节点放入原来的队列;
(3)重复(2)的步骤,直到队列中只有一个节点,此节点为根节点;
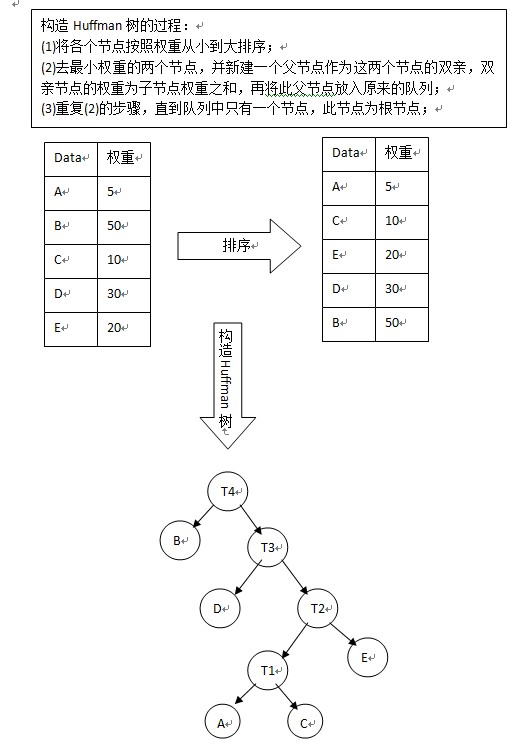
构造完Huffman树之后,就可以进行Huffman编码了,编码规则:
(1)左分支填0,右分支填1;

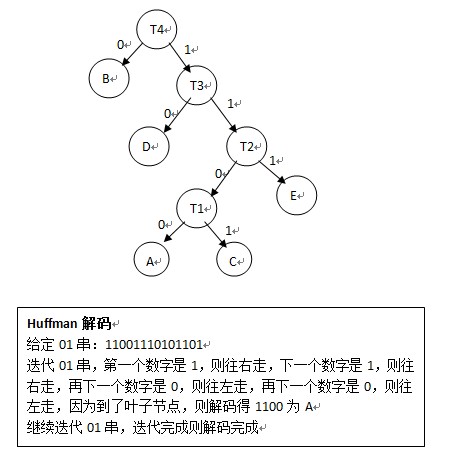
Huffman解码过程
(1)给定一个01串,将01串进行Huffman树,到叶子节点了就表明已经解码一个节点,然后再次遍历Huffman树;