1. 曲率基本概念
曲率是几何体不平坦程度的一种衡量。
- 曲线曲率
曲线曲率可以描述曲线的弯曲程度,在曲线方程知道的情况,且二阶导存在的情况下(直角坐标系),其值为
\[K=\frac{\left | y^{''} \right | }{(1 + {y^{'}}^{2})^{\frac{3}{2} }}
\]
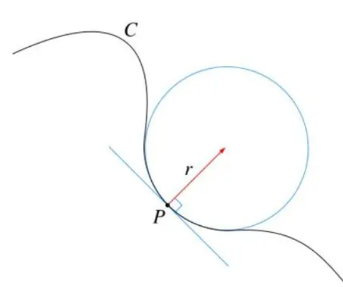
曲率与曲率半径成倒数关系,如下图P点的曲率半径为
\[r = \frac{1}{K}
\]
2. 三角网格顶点的曲率
在三角网格模型中,估计顶点曲率经常被用到,可以先估计出该顶点附件的曲面方程,然后再求曲率;也可以直接按照顶点周围的邻接关系进行估算。这里记录一下一些估算曲率的方法。
-
离散方法
三角网格上高斯曲率和平均曲率的计算
三角网格上高斯曲率和平均曲率的计算
相关讨论
CurvaNet
TriMesh_curvature 对应论文《Estimating Curvatures and Their Derivatives on Triangle Meshes》
3. 有序离散点曲率近似
根据当前点,找出一点前后距离的点,然后估算出曲率
点击展开部分代码
double GetEdgeLength(size_t indx, size_t nextIndex, const std::vector<core::Vector3>& ori, std::vector<double>& edgeLengthArray)
{
if (edgeLengthArray[indx] < 0.0)
{
edgeLengthArray[indx] = (ori[indx] - ori[nextIndex]).Magnitude();
}
return edgeLengthArray[indx];
}
double ComputeNormalizedCurvature(const std::vector<core::Vector3>& ori, size_t indx, std::vector<double>& edgeLengthArray, double neighborSize = 1.8)
{
const core::Vector3& thisPt = ori[indx];
double currentDis = 0.0;
size_t currentIndex = indx;
while (currentDis < neighborSize)
{
size_t nextIndex = currentIndex - 1;
if (currentIndex <= 0) {
return 0.0; // the last
}
currentDis += GetEdgeLength(nextIndex, currentIndex, ori, edgeLengthArray);
currentIndex = nextIndex;
}
const core::Vector3& lastPt = ori[currentIndex];
currentIndex = indx;
currentDis = 0.0;
while (currentDis < neighborSize)
{
size_t nextIndex = currentIndex + 1;
if (nextIndex >= ori.size())
return 0.0; // the last
currentDis += GetEdgeLength(currentIndex, nextIndex, ori, edgeLengthArray);
currentIndex = nextIndex;
}
const core::Vector3& nextPt = ori[currentIndex];
core::Vector3 lineDir = lastPt - nextPt;
double l = lineDir.Magnitude();
lineDir *= 1.0 / l;
double d = core::Distance::PointLine(thisPt, lastPt, lineDir);
return d / l;
}
inline bool IsPeak(double lastValue, double thisValue, double nextValue)
{
return lastValue < thisValue&& nextValue < thisValue;
}