数据结构5——二叉树（1）

1：二叉树的建立

二叉树的建立有两种模式：（1）：首先设计二叉树的结点类，然后在此基础上，用static成员函数实现二叉树的具体操作。

　　　　　　　　　　　　（2）：设计二叉树的结点类，然后在二叉树的结点类的基础上设计二叉树类。

/*
 * 定义一个二叉树的结点类
 */
public class BinTreeNode {
    private BinTreeNode leftChild;
    private BinTreeNode rightChild;
    private Object data;
    
    public BinTreeNode(){
        leftChild=null;
        rightChild=null;
    }
    
    public BinTreeNode(BinTreeNode left, BinTreeNode right,Object Idata){
        leftChild=left;
        rightChild=right;
        data=Idata;
    }

    public BinTreeNode getLeftChild() {
        return leftChild;
    }

    public BinTreeNode getRightChild() {
        return rightChild;
    }

    public Object getData() {
        return data;
    }
}

设计完了二叉树的结点类之后，在二叉树的结点类的基础上用static成员函数实现二叉树的具体操作。

包括二叉树的生成，二叉树的打印，二叉树的遍历，在二叉树中查找元素。

(1）首先在二叉树结点类的基础上构建二叉树。结构如上图所示：

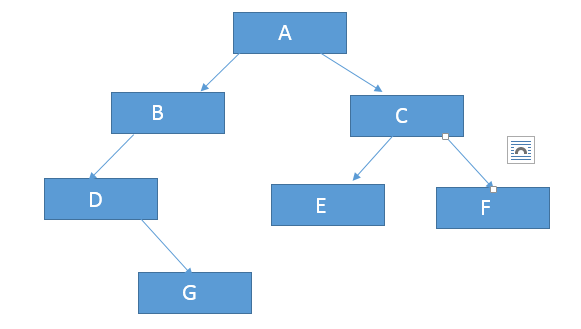
先构造一个方法用于获得二叉树的结点类

//获得一个二叉树结点的类
    public static BinTreeNode getTreeNode(Object item, BinTreeNode left, BinTreeNode right){
        //构造一个二叉树
        BinTreeNode temp=new BinTreeNode(left, right, item);
        return temp;
    }

//在结点类的基础上构造一个二叉树
    public static BinTreeNode makeTree(){
        BinTreeNode a,b,c,d,e,f,g,h;
        
        g=getTreeNode(new Character('G'), null, null);
        d=getTreeNode(new Character('D'), null, g);
        b=getTreeNode(new Character('B'), d, null);
        e=getTreeNode(new Character('E'), null, null);
        f=getTreeNode(new Character('F'), null, null);
        c=getTreeNode(new Character('C'), e, f);
        return getTreeNode(new Character('A'), b, c);
    }

（2） 打印一棵二叉树

//打印二叉树，主要将纵向的二叉树横过来，基本的思维是先打印右子树，根节点，左子树
    public static void printBiTree(BinTreeNode root, int level){
        if (root!=null) {
            //根节点root的level+1层开始输出右子树，不断的递归调用
            printBiTree(root.getRightChild(), level+1);
            
            if (level!=0) {
                for(int i=0; i<6*(level-1); i++){
                    System.out.print(" ");
                }
                System.out.print("---");
            }
            System.out.println(root.getData());         //输出结点数据元素的值
            
            //根节点root的level+1层开始输出左二叉树，不断的递归调用
            printBiTree(root.getLeftChild(), level+1);
        }
    }

（3）：查找二叉树中的某个元素

//定义一个方法在二叉树中查找某个(x)元素
    public static BinTreeNode search(BinTreeNode t,Object x){
        
        BinTreeNode temp;
        if (t==null) return null;                //查询失败
        if (t.getData().equals(x)) return t;     //查找成功返回某个子二叉树
        
        //在左子树寻找元素
        if(t.getLeftChild()!=null){
            temp=search(t.getLeftChild(), x);
            if (temp!=null) return temp;
        }
        //在右子树中寻找元素
        if(t.getRightChild()!=null){
            temp=search(t.getRightChild(), x);
            if (temp!=null) return temp;
        }    
        return null;        //查询失败的出口
    }

（5）：实现二叉树中最重要的遍历，用递归的方法实现。当然后面肯定有非递归的方法。

首先需要定义一个访问二叉树结点的方法

/*
 * 定义一个类用于打印输出每个结点
 */
public class Visit {
    public void print(Object item){
        System.out.print(item+" ");
    }
}

/*
 * 定义一个用于遍历二叉树的类
 */
public class BinTraverse {
    
    //前序遍历
    public static void preOrder(BinTreeNode t, Visit v){
            //如果是非递归的方法遍历二叉树，此时这里面的if 还能用if吗？
        if (t!=null) {
            v.print(t.getData());
            preOrder(t.getLeftChild(), v);
            preOrder(t.getRightChild(), v);
        }
    }
    
    //中序遍历
    public static void inOrder(BinTreeNode t, Visit v){
        if (t!=null) {
            inOrder(t.getLeftChild(), v);
            v.print(t.getData());
            inOrder(t.getRightChild() , v);
        }
    }
    
    //后序遍历
    public static void postOrder(BinTreeNode t, Visit v){
        if (t!=null) {
            postOrder(t.getLeftChild(), v);
            postOrder(t.getRightChild(), v);
            v.print(t.getData());
        }
    }
    
    //层序遍历,层序遍历的基本原理是，每遍历一个根节点则进去左右两个孩子节点
    //逻辑类似于队列，先进先出
    public static void levelOrder(BinTreeNode t, Visit v) throws Exception{
        LinQueue lq=new LinQueue();　　　　　　　　　　　　　　　　　　//这里面需要链式队列的类型
        
        if (t==null)  return;
        BinTreeNode curr;
        lq.append(t);
        while (lq.notEmpty()) {
            curr=(BinTreeNode) lq.delete();            //从队列中删除根节点，并且将队列转化为二叉树的一个结点
            v.print(curr.getData());                //并且输出该节点的值
            //将左右结点分别插入到队列中
            if (curr.getLeftChild()!=null) 
                lq.append(curr.getLeftChild());
            if (curr.getRightChild()!=null) 
                lq.append(curr.getRightChild());
        }
    }
}

    /*
     * main函数 
     */
    public static void main(String[] args) {
        BinTreeNode root1;
        BinTreeNode temp2;
        
        Visit v=new Visit();
        
        root1=makeTree();
        System.out.println("二叉树为： ");
        printBiTree(root1, 0);
        System.out.println();
        
        
        System.out.println("前序遍历节点序列为：");
        BinTraverse.preOrder(root1, v);
        System.out.println();
        
        System.out.println("中序遍历节点序列为：");
        BinTraverse.inOrder(root1, v);
        System.out.println();
        
        System.out.println("后序遍历节点序列为：");
        BinTraverse.postOrder(root1, v);
        System.out.println();
        
        
        //查找某个元素
        temp2=search(root1, new Character('F'));
        if (temp2!=null) {
            System.out.println("查到该节点的数据元素为： "+temp2.getData());
        }
        else{
            System.out.println("查找失败！");
        }

 **************上面说道二叉树的建立，有两种方法，下面实现第二种方便生成二叉树，在结点的基础之上建立二叉树的类。**********

（1）二叉树结点类

/*
 * 定义一个二叉树的结点类
 */
public class BinTreeNode {
    private BinTreeNode leftChild;
    private BinTreeNode rightChild;
    private Object data;
    
    public BinTreeNode(){
        leftChild=null;
        rightChild=null;
    }
    
    public BinTreeNode(BinTreeNode left, BinTreeNode right,Object Idata){
        leftChild=left;
        rightChild=right;
        data=Idata;
    }

    public BinTreeNode getLeftChild() {
        return leftChild;
    }

    public BinTreeNode getRightChild() {
        return rightChild;
    }

    public Object getData() {
        return data;
    }
}

在二叉树结点类的基础上实现二叉树

/*
 * 先在二叉树结点类的基础上，设计二叉树类
 */
public class BinTree {
    private BinTreeNode root;                //根指针
    
    
    //前序遍历
    public void preOrder(BinTreeNode t, Visit s){
        if (t!=null) {
            s.print(t.getData());
            preOrder(t.getLeftChild(), s);
            preOrder(t.getRightChild(), s);
        }
    }
    
    //中序遍历
    public void inOrder(BinTreeNode t, Visit s){
        if (t!=null) {
            inOrder(t.getLeftChild(), s);
            s.print(t.getData());
            inOrder(t.getRightChild(), s);
        }
    }
    
    //后序遍历
    public void postOrder(BinTreeNode t, Visit s){
        if (t!=null) {
            postOrder(t.getLeftChild(), s);
            postOrder(t.getRightChild(), s);
            s.print(t.getData());
        }
    }
    
    //构造函数用于初始化root结点
            public BinTree(){
                root= null;
            }
            
            //构造函数用于处理一个二叉树
            public BinTree( BinTree left, BinTree right,Object item){
                BinTreeNode leftNode;
                BinTreeNode rightNode;
                
                if (left==null) {
                    leftNode=null;
                }else{
                    leftNode=left.root;　　　　　　　　        //让左子树获得左子树的结点
                }
                
                if (right==null) {
                    rightNode=null;
                }else{
                    rightNode=right.root;
                }
                
                root=new BinTreeNode(leftNode, rightNode, item);
                
            }    
    
    //前序遍历 在二叉树类遍历的基础上，调用二叉树结点遍历方法还是让二叉树结点类实现递归作用，因为最终遍历的都是书的结点
    public void preOrder(Visit vs){
        preOrder(root, vs);
    }
    
    //中序遍历
    public void inOrder(Visit vs){
        inOrder(root, vs);
    }
    
    //后序遍历
    public void postOrder(Visit vs){
        postOrder(root, vs);
    }
}

 写一个测试类，包括二叉树的建立，以及二叉树的遍历。

public static void main(String[] args) {
        
        //构造第二种方法的二叉树
        BinTree g=new BinTree(null, null, new Character('G'));
        BinTree d=new BinTree(null, g, new Character('D'));
        BinTree b=new BinTree(d, null, new Character('B'));
        BinTree e=new BinTree(null, null, new Character('E'));
        BinTree f=new BinTree(null, null, new Character('F'));
        BinTree c=new BinTree(e, f, new Character('C'));
        BinTree a=new BinTree(b, c, new Character('A'));
        
        
        Visit v=new Visit();
        
        System.out.print("前序遍历结点序列为：");
        a.preOrder(v);
        System.out.println();
        
        System.out.print("中序遍历结点序列为：");
        a.inOrder(v);
        System.out.println();
        
        System.out.print("后序遍历结点序列为：");
        a.postOrder(v);
        System.out.println();
    }

大体的实现就是这样，还是感叹一句啊，在能够完全理解的情况下还是要多敲代码啊！！！！

No more talking,show me coding!!

下一节：非递归的二叉树遍历。