Adaboost(Adaptive boosting)是boosting(提升)家族的重要算法。boosting家族算法的核心是串行训练学习器,可以理解为"站在巨人的肩膀",后一个学习器的学习是基于前一个学习器的学习基础之上的,对应的是bagging学习器,学习器之间没有依赖关系。
把握住Adaboost算法核心是获取两个权重:一个是样本权重ω(仅用于构建模型阶段),一个是弱学习器参数α(用于构建模型阶段以及模型预测阶段)。
Adaboost基本流程描述
我们先来了解一下boosting的基本流程:
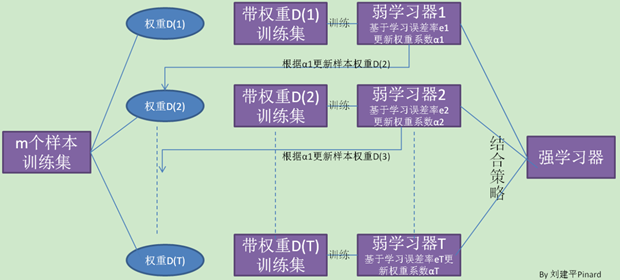
先来过一下Adaboost学习的全流程:
拥有数据集T={(x1, y1), (x2, y2), (x3, y3),... (xm, ym)};
第一步:设置样本权重
初始化样本权重(sample weight)D={ω11, ω12,...,ω1m}, ω1i = 1/m;权重之和=1,不仅仅是初始化,后面的标准化目的都是要保证ω之和为1;
第二步:训练数据
使用数据T训练模型,同时传入样本权重D,比如如果弱学习器采用的是决策树(Decision Tree),则是在调用fit(T, D)。
第三步:计算学习器权重
模型训练出来之后,需要计算一下该模型(学习器)的权重,为了计算权重首先计算一下错误率(统计所有的样本的):
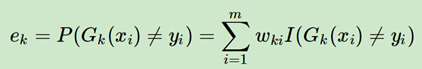
ωki这里代表的样本i(共有m个样本)在第k轮学习器训练中的权重,这里I(·)是一个指示函数,代表如果Gk(xi)≠yi,则I(·)值为1,反之为0;判断错误的样本的权重之和就是错误率;
这里我曾经有困惑,既然Gk使用X训练出来的,就应该能够完全匹配啊;其实不然,决策树节点划分不是匹配,而是基于增益,那个特征值作为划分节点能够实现最大增益,就是有对的,有错的,但是选择A.a作为划分节点能够使得分类最为稳定(确定);其实即使是最终学习的结果,也还是每个叶子节点有有多种分类只不过概率不同而已,你在使用决策树的时候,预测有两个函数,一个是predict,返回概率最大的那个,predict_probability,返回定位的叶子节点的各个分类概率。所以这里既是是用训练样本训练出来的Gx,仍然会有一定错误率。
下面的公式是用来计算学习器(Gk(x))的权重。
αk = (1/2)log[(1 - ek)/ek]
通过上面的公式我们可以知道ek越大,αk的值越小,即错误率越高的学习器,权重会比较小,这一点符合预期。如果我们在细分析一下,你会发现当ek = 0.5的时候(错误率是一半)是一个分界点,此时αk = 0;这意味着ek<=0.5,有αk >= 0。反之,如果ek>0.5(比较高的错误率),那么αk < 0。
重回第一步:设置样本权重
这里其实又回到了第一步,设置下一轮学习器的权重,只不过此时不再是第一步的取平均值,完成当前轮的学习之后要更新下一轮学习的样本权重,公式如下式所示:
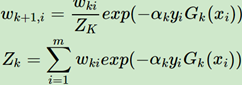
这里的Zk就是一个标准化因子,目的是让Σωk+1,i = 1,所以你可以看到Zk的项公式其实和ωk+1分子的形式是一模一样的。对于ωk+1,i是有两种结果(截图中m就是上图这个的k):
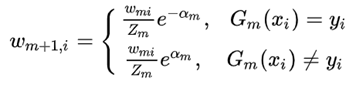
分类正确 => ωk+1,i = ωk,i * exp(-αk) 以及 exp(-α) < 0 => 权重值减小;
分类错误 => ωk+1,i = ωk,i * exp(αk) => 分类错误,权重增加。
备注一下,yi和Gk(xi)返回的都是±1,所以相乘结果也是±1,同号(判断分类结果一直)则为1,异号(分类结果不一致)则为-1,这里分类结果是∈[-1, 1],和逻辑回归以及很多分类函数∈[0, 1]不一样,注意一一下。
然后基于这个样本权重进行下轮学习和模型Gk+1(x)的构建。
需要强调一下,boosting学习器里面获取重点是训练样本的权重,是的,每一个样本的权重;其实boosting里面的弱学习器之间并没有强弱之分,差别的本质在于他们所学的样本,虽然样本都是一套(所有的弱学习器都是同一套样本训练出来的,所以学习器本身没有优良之分),但是样本的权重却是不同的,对于决策树(adaboost的弱学习器一般选择决策树或者神经网络),在进行节点拆分,分析特征值的时候,都会使用特征值*权重之后来进行分析。
adaboost是一个迭代算法,是通过多轮学习来构建模型;比如目标是训练出来K个学习器那么就需要学习K轮;
最后一步:获取强学习器
最后经过N轮学习之后,会收获N个弱学习器,最终模型如下:
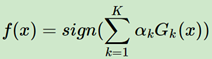
这里是二元分类的模型函数,最终根据函数的正负号来判断分类。其中αk是学习器的权重,Gk(x)则是学习器的(一颗决策树或者一个神经网络)。累加权重学习器的值,根据正负号来进行分类。
弱学习器开始的时候因为样本*权重的分布问题,开始错误率将会非常高,但是后来随着权重不断的优化,权重样本的分布将会越来越合理,错误率将会越来越低。不过注意,作为adaboost的学习器,最终的结果是各个学习器结果*学习器权重之后来获取的,对于早期的学习器他们的权重αk值将会很低,后来随着错误率的减小,权重将会越来中。
Adaboost原理 - αm的推导
αm的推导要从理解Adaboost分类算法以及损失函数说起,可以用三个点来描述:
1. 加法模型;
2. 分步向前;
2. 指数损失函数;
第一个加法模型没有问题,因为我们的目标函数是弱学习器和权重乘积之和:
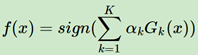
第二个分步向前,每一轮的强学习器的结果的获取,都是基于之前累积的结果,数学表达如下:

根据上面两个表达式,可以推知:
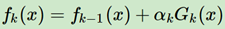
第三个是损失函数为指数函数,有了前面两个作为基础,我们再来看一下Adaboost是如何基于损失函数形式来推导αm(弱学习器权重),这里强调一下这里推导的弱学习器的权重α是指指定的k轮的学习器Gk的权重,针对特定的学习器的权重:

对于fk,基于分步向前推导,可以对其进行fk-1的变形:
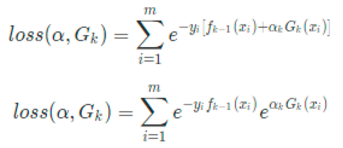
这里因为已经推倒到了k轮,所以fk-1和yi都是常量,所以我们把它简化设置为ω':
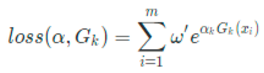
我们首先来求解一下Gk(x):
Gk(x) = argmin Σw' * I(yi ≠ f(xi))
这个Gk公式说明了如果正确分类了yi*Gk(xi) = 1,否则yi*Gk(xi) = -1;这里解释一下,对于二元分类而言,yi = ±1,弱学习器比如决策树,Gk(xi) = ±1,所以yi*Gk(xi)一定是只能=±1。
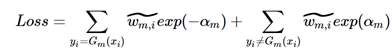
此时损失函数成为了两部分之和,一部分是弱学习器正确分类部分,另外一部分是错误分类部分。然后对其进行标准化,有:
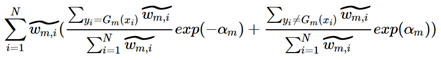
这一步的演化我花了很长时间才明白,注意上上式的Loss的Σ的范围是yi=Gm(xi)以及yi≠Gm(xi),到了上式取值范围扩充为了i=[1, N],其实两个式子是等价的,在i=[1, N]的范畴内,表达y=Gm(xi)的频率就是下式,其实是不是ω_hat并不重要,替换为1也是可以的(因为分子分母的数据sum的值是一样的,是累计的数量不同而已):
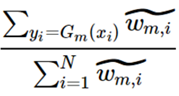
但是这里有一个问题,为什么概率表现形式是它呢?如果是概率的话,应该就是错误的数量比上总数量即可啊。我觉得这个就是样本权重的意义,就是正常样本的权重是1,我们在计算概率的时候就是:数量/总数,但是对于赋予了权重之后,样本就不再是一个样本的概念,可能一个样本顶N个样本,或者不足一个样本。
在i=[1, N]的范围内表达yi≠Gm(xi)与之类似:
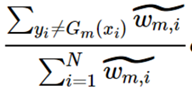
除此之外,你还会发现上式其实就是ek的表达式,那么上上式就是1-ek的表达式,也是Loss可以简化表达为:
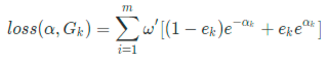
ek其实就是错误的概率或者说频率(即,N_error/N_total),然后对Loss的α求导(虽然外部是Σ,但是对于αk求导只会有一个式子包含αk):
![]()
这里注意exp(-α)求导后变成了exp(α)(自然指数的导数还是其自身,但是符号将会被提取出来),Loss里面的(1 - ek)变成了(ek -1)。令导数 = 0,有
ω = 0 或者(ek-1) * exp(αm) + ek * exp(αm) = 0
这里注意exp(-α)求导后变成了exp(α)(自然指数的导数还是其自身,但是符号将会被提取出来),Loss里面的(1 - ek)变成了(ek -1)。
继续,我们推到(ek - 1) * exp(αm) + ek * exp(αm) = 0,两边去对数(ln)有:
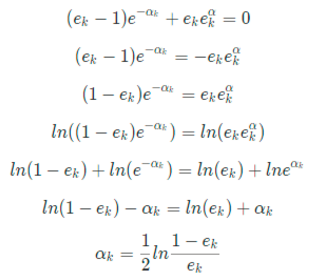
Adaboost正则化
原始公式如下:
fk+1(x) = fk(x) + αkGk(x)
添加正则项就是在最后一项增加系数v
fk+1(x) = fk(x) + vαkGk(x),v∈[0, 1]
Adaboost背后原理未知
但是这里有一个问题,adaboost其实本质是通过改变样本的分布来提高弱学习器的分类能力;那么未来新的数据到来如果不符合历史的数据分布怎么办呢?那么预测的结果是不是会偏差比较大呢?Adaboost背后的原理还是需要深入搞清楚。
参数设置(sklearn)
弱学习器类型指定
通过base_estimator,默认分类是CART分类树,回归是CART归回树;如果是其他需要注入如果算法指定了SAMME.R,这里指定的学习器需要支持概率预测。也就是模型(学习器)支持predict_proba函数。
SAMME vs. SAMME.R
SAMME和SAMME.R都是sklearn里面实现Adaboost的分类算法,默认SAMME.R,该算法采用的基于样本集的预测概率作为机器学习权重,这个和SAMME的基于样本集分类结果为基础来计算权重算法有不同,但是.R的方法计算速度会快一些,所以.R作为了默认的算法。在sklearn里面可以通过algorithm参数来指定相应的算法。
弱学习器的数量
通过n_estimator来进行指定(和随机森林里面要创建几棵树的参数名一样)。
Adaboost的多分类
Adaboost的多分类有M1和M2算法,M1算法是基于Adaboost的二元分类算法的,只是在模型函数(H(x))以及学习器权重公式(βt)以及样本权重公式(Dt)做了修改,使之适应多分类;M2算法基于M1,不过更加复杂;这里没有使用经典的softmax类型,以及oneOone等方式,可以在附录区看一下相应算法流程。
Adaboost的回归算法
Adaboost的回归算法种类比较多,但是其思想和分类是一样的,基本流程都是为样本权重赋值,训练弱学习器,计算学习器的权重,基于学习器的权重更新样本权重,在继续训练学习器,直到迭代结束。
不同的地方在于因为他们损失函数以及错误率计算方式不一样,所以学习器的权重公式不同,另外就是最后获得模型组成也是和分类器不同。
具体的可以参见参考中的刘建平博客连接,在介绍Adaboost的时候提到了回归的算法R2.
附录
对数性质
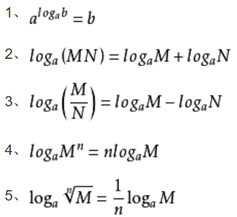
Adaboost多分类算法

参考:
https://www.cnblogs.com/pinard/p/6133937.html 刘建平的adaboost说明
https://www.cs.utexas.edu/~dpardoe/papers/ICML10.pdfAdaboost回归算法论文
https://zhidao.baidu.com/question/365096902.html 指数取对数公式
详细的手推过程
https://www.cnblogs.com/ScorpioLu/p/8295990.html
https://blog.csdn.net/weixin_38381682/article/details/81275905
https://blog.csdn.net/v_july_v/article/details/40718799
Adaboost的多分类
https://blog.csdn.net/tyh70537/article/details/76675098

Adaboost的回归算法Adaboost的回归算法种类比较多,但是其思想和分类是一样的,基本流程都是为样本权重赋值,训练弱学习器,计算学习器的权重,基于学习器的权重更新样本权重,在继续训练学习器,直到迭代结束。不同的地方在于因为他们损失函数以及错误率计算方式不一样,所以学习器的权重公式不同,另外就是最后获得模型组成也是和分类器不同。具体的可以参见参考中的刘建平博客连接,在介绍Adaboost的时候提到了回归的算法R2.