解决问题
实现基于特征范围的树状遍历的回归。
解决方案
通过寻找样本中最佳的特征以及特征值作为最佳分割点,构建一棵二叉树。选择最佳特征以及特征值的原理就是通过满足函数最小。其实选择的过程本质是对于训练样本的区间的分割,基于区间计算均值,最终区域的样本均值即为预测值。
在预测的时候,将会根据提供的样本的特征,来遍历二叉树(确定区域的过程),其中叶子节点的值就是预测值。
构建回归决策树,过程,其实可以理解对训练样本进行监督式聚类,每个分类都是有一组特征逻辑范围做描述;预测的时候,其实就是在匹配,那个分类逻辑范围路径和预测样本匹配,然后取这个分类里面的y值均值作为预测值。
因为决策树每一步都是当前损失函数的最优解,所以本质还是贪心算法,因为每一步都是局部最优;所以CART的回归算法也是一种启发式算法的范畴。
所以,决策树的构建过程本质就是两步走:
1. 对于一个特征值序列进行各个点位的二分,计算每一次二分之后的两个点位的残差平方和(yi和mean(yi)的残差),选择最小的那个特征值作为候选分割点;
2. 在针对候选的分割点的选出残差平方和最小的作为当前层的分割点。
其实无论是决策树回归还是分类,你会发现决策树解决思路都是一样的,遍历所有的特征的特征值,来作为分割点,然后看哪一个分割点的效果最好,在分类里面看的是信息增益(C3),信息增益比(C4.5)以及gini指数(CART),回归(CART)就是看孩子节点的残差平方和之和;然后再在各个孩子节点中继续选择分割点,直到层次达到了指定或者孩子节点只有一个样本。
实现
通过下面的公式可以看出来解决方案的实现,因为CART的回归,所以解决的思路求得是损失函数的最小值,如下式所示:

这里套了两层min,第一min是各个特征在自己的特征值层面上选出最小值,即各个特征选出最佳分割特征值,外层min则是在各个特征层面上,选择误差最小的特征,这样选出了“最佳”的分割特征值,最佳打引号是因为决策树这种方式是启发式,并不一定是全局最佳,只是局部最佳。
R1和R2两个区域代表的是二叉树(j特征的特征值s作为逻辑判断条件)所划分的两个区域(样本集合);j代表的是样本x的第j个特征(是一个索引值),xj代表的是x第j个特征的特征值;s则代表j的指定特征值。
R1(j, s) = {x | xj ≤ s}, R2(j, s) = {x | xj > s}
c1和c2则是叶子节点的样本值,下面的式子代表枚举叶子节点所有的样本值c,获取其取值范围,在这个范围内来计算yi - c,取(yi-c)²的最小值。

这个c的最佳值(满足(yi -c)²最小)是c值的均值(这个可以通过求导值为0计算出来,c值为y的均值),上式可以写成(将minC1/ minC2的约束改为具体的值:c1_hat和c2_hat,_hat代表估算的最佳值,即均值)下面的公式,注意,里面的min算子消失了,c变成了c_hat:
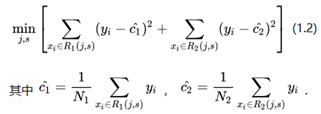
最终我们构建的决策树的模型是:
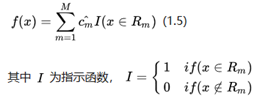
关于f(x)的公式,我们看下面的图会更加直观,回归决策树本质其实就是为样本划分区域,在遍历树种非叶子节点的过程就是在逐渐的细化范围,以下图为例,首先是选择一个最佳点进行二分划分(图中黑色实线部分),然后再这对每一部分,在寻找各自的最佳二分点进行二次划分(图中虚线部分),最后到了叶子节点其实就是每个被细化的区域区域了。

区域里面的(训练)样本y值的均值就是这个区域的值(x值即特征值用于区域划分)。从这个视角我们再来看f(x)=Σcm_hat * I,cm_hat就是区域的均值(叶子节点值),I是一个只是函数,如果是带预测样本是在该区域,I值为1,否则为0。这个函数其实就是用来定位(唯一)区域的。
这个模型看起来有些抽象,看一下决策树回归的图形,首先来一张树状图:
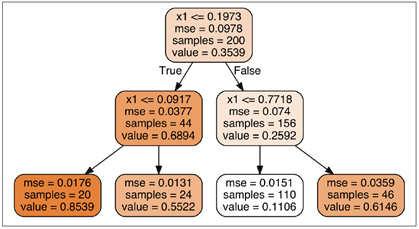
下图左侧就是上图对应的数据展示,最后一层叶子节点因为没有区分度,所以不算一层,只有包含父节点的才算一层。

通过上图可以看出来,决策树的图形其实是在指定的范围内的值为直线,这个范围就是每个节点的条件。
我们先来看一下左侧的depth为2的图:根节点是0.2作为分割线,即靠左侧的实线线,将整个样本空间一分为二,R1:(0,0.2), R2:(0.2, 1.0);然后是第二层两个子节点,分别是0.1和0.8(近似值),将根节点所划分的区域继续一分为二,这样就有了四个区域;每个区间都有自己的R空间(样本),其中的红线就是各个空间里面样本的应变量的均值,即cm值。通过这种方式划分,其实实现了损失函数值最小。
我们再来看一下右侧图,即depth=3,你会发现一个特点,任何一个R区间都会包含一个最后一层,这是因为最后获取叶子节点,这是因为每个子节点(非叶子)一定回事把所有的父节点所划分的区域一分为2,所以所有的区域一定是有最有一层节点对应的分割线的。
总之,我们会发现决策树其实是通过阶梯式的图像,来拟合训练空间的样本(一定程度上是有一些生硬的。所以做回归,一般很少直接使用CART,而是CART的簇,随机森林)。
那么我们再回到公式,我们就拿左侧图(depth=2)来举例,对于f(0.5),这个值只会属于其中一个R空间,这里是(0.2,0.8)区域,所以其他区域在公式计算中都应该取值为0,这个就是指示函数的作用,类似于开关作用,确保只有应该计算点是有值,其他都是0值。
实际案例
下面通过一个实际的例子来解释一下这个求解过程。
下面的图标是某个特征j的特征值:

需要考虑如下9个切分点:{1.5, 2.5, 3.5, 4.5, 6.5, 7.5, 8.5, 9.5},这里切分点是取相邻的两个特征值的均值。
对于第一个切分点1.5,y值数据(5.56)为第一个数据区域R1,2.5~9.5为第二个数据区域R2。
于是有c1 = 5.56,c2 = (1/9)*Σyi = 7.5
L(1.5) = (y1 - 5.56)² + Σ(yi - c2)² = 15.72,这里 i∈[1, 9]
继续,按照第二个切分点2.5,R1={5.56, 5.7},R2={5.91, 6.4,..., 9.05},于是有:
c1 = mean(R1) = 5.63, c2 = mean(R2) = 7.73
L(2.5) = Σ(yi - c1)² + Σ(yj - c2)² = 12.07,其中i∈[0, 1],j∈[2, 9]
以此类推有:

我们看到该属性损失函数最小的是6.5这个点,于是对于该属性最佳区分点就是6.5。于是有(这里的R采用x:y模式来表示):
R1={1:5. 2:56, 3:5.7, 4:5.91, 5:6.4, 6:7.05}, R2={7:8.9, 8:8.7, 9:9, 10:9.05}
如果该样本还有其他属性,也是以此类推,计算出来各个最佳区分点的L(s),然后选出L(s)值最小的特征以及区分点,作为二叉树的节点;然后提出到选定的特征,再从R1和R2中继续该操作分别获得新的子节点,循环往复。
附录
为什么c1_hat和c2_hat的最优解是对应的均值呢(注意,带hat代表该值是估计值)?
这里我们看一下推倒的过程:
F(a) = (x1 - a)² + (x2 - a)² + ... + (xn - a)²
考察其单调性(通过求导来求其极值):
F'(a) = -2*(x1 - a) - 2(x2 - a) - ... - 2(xn - a) = 2na - 2*Σxi(此处注意,因为是对a求导,a前面是-号,所以求导后系数为-2)
F'(a) = 0 => a = (1/n)*Σxi
根据其单调性,可以知道a_hat = (1/n)*Σxi为最小值。
根据公式来看求得是L2的值,所以构建的树也称之为最小二乘回归树。
单调性为什么可以通过求导体现出来,怎么体现出来?
导数代表的是函数变化速率,单调性代表了y值和x值变化是否是同方向,同方向则>0,反方向则<0;基于这个理解,不难退出导数如下定理:
f'(x) > 0 => f(x)是增函数(单调递增)
f'(x) < 0 => f(x)是减函数(单调递减)
f'(x) = 0 => f(x)是常数函数。
注意,这个左侧条件为充分条件而非必要条件,单调增减并不推导出函数导数的正负性。
导数怎么来判断极值的,是极大值还是极小值?
首先要明白一点,极值是一个局部概念,只是描述某个点两边的变化趋势。
首先导数=0,称之为函数的驻点,然后分析驻点两边的导数值是否异号,如果异号:左边区域>0,右边区域<0 =>驻点是极大值(峰值,可以想象沿着x轴正方向,山峰的左侧是上行,右侧是下行),反之是极小值(谷底值,可以想象,沿着x轴正向,山谷左侧是下行,右侧是上行)。如果驻点两侧同号,则称该点为鞍点:
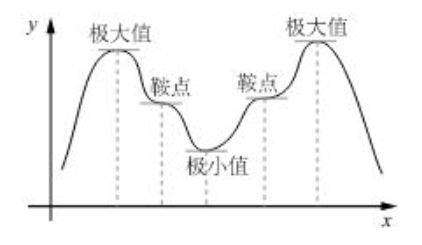
导数的峰值分析,一般思路:
1. 求导数公式,令导数为0,求出驻点;
2. 基于驻点和指定的区间,以驻点为截线将x轴进行区域分割,分析驻点两边导数正负号,来决定驻点的是否为极值点或者说为哪一类极值点。
下面举一个例子:
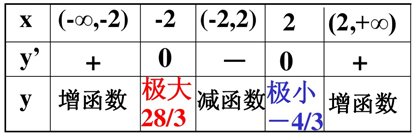
y = (1/3)*x³ - 4x + 4
求导:y' = x² - 4 = (x+2)*(x-2)
求驻点:y' = 0 = (x + 2)*(x - 2) => x= ±2
划分区域,分段分析极值:
参考
https://zhuanlan.zhihu.com/p/42505644
https://blog.csdn.net/weixin_40604987/article/details/79296427
https://www.jianshu.com/p/b90a9ce05b28
https://wenku.baidu.com/view/eb97650e76c66137ee061960?fr=uc 导数极值例子参考
https://wenku.baidu.com/view/4357a7ce58f5f61fb73666c3?fr=uc 提到了极值只是局部概念
https://blog.csdn.net/wfei101/article/details/80766934 提到了驻点概念

其实无论是决策树回归还是分类,你会发现决策树解决思路都是一样的,遍历所有的特征的特征值,来作为分割点,然后看哪一个分割点的效果最好,在分类里面看的是信息增益(C3),信息增益比(C4.5)以及gini指数(CART),回归(CART)就是看孩子节点的残差平方和之和;然后再在各个孩子节点中继续选择分割点,直到层次达到了指定或者孩子节点只有一个样本。