核函数的起源是对于线性不可分的分类情况,其实可以通过p次方多项式,及非线性模型进行分类;然后对于这类非线性多次方的,其实可以按照广义线性模型来进行升维变形,使之成为线性模型,这样就可以放到SVM中来进行处理了(svm只能处理非线性模型)。
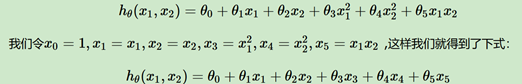
但是升维之后是有维度爆炸现象的(二次方对应6维度,三次方对应19维度),为了解决这个问题,核函数出场了,简单讲核函数就是计算计算是在低维进行,但是形式却是映射到高维。
SVM的优化目标:
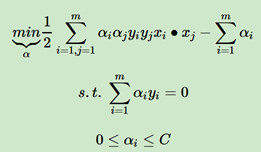
假设xi和xj都是低维非线性的函数,我们定义映射到高维的函数为φ(x),那么上面的式子可以写成:
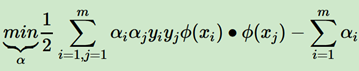
核函数,就是实现了计算在低维计算,返回形式是高维:
K(x, z) = φ(x) * φ(z)
但是这种映射并不是容易获取的,需要满足Gram矩阵K = [K(x,z)]是半正定型,也就是说,一个函数想要成为核函数,必须要满足里面任何点的集合形成的Gram矩阵是半正定矩阵。
这里解释一下,gram矩阵是指n维欧式空间中任意k个向量内积组成的矩阵:

关于正定矩阵:M是n阶方阵,对于非0向量,z.T *M*z > 0,矩阵的乘法还是矩阵,这里> 0,我理解是因为乘法形式的行列式的值是大于0的。
半正定矩阵和正定矩阵就是一字之差:z.T * M * z >= 0,半正定允许等于0,所以范围更加宽广,所以血统不那么纯正,所以称之为半正定(越纯正要求越严格)。
话题再扯回来,如果想要满足核函数,那么函数K的矩阵要满足Gram矩阵是半正定的;这个门槛其实很高的,好在我们数学大佬们已经带我们走出探索的沼泽,并且亲自指出了常用的核函数与:
线性核函数(Linear Kernel):
K(x, z) = x·z,线性svm就是使用这个核函数;
多项式核函数(Polynomial Kernel):
k(x, z) = (γx·z + r)^d,其中gamma,r以及d需要自己调参;
高斯核函数(Gaussian Kernel),也称之为径向基和函数(Radial Basis Function,RBF):
K(x, z)=xp(−γ||x−z||²)
Sigmoid核函数:
K(x,z)=tanh(γx∙z+r),其中γ和r需要自己调参;
参考: