向 CXY 学习!
大概一天尽量更 3 道题,鸽了可以催一催,说不定就更了(
标签:
(color{red}{12345}):代码难度,(color{blue}{12345}):思维难度,(color{green}{12345}):巧妙程度/优美程度。
(dagger):已完成,暂鸽,(Psi):未完成。
T1 CF504E Misha and LCP on Tree (color{red}3color{blue}1color{green}1)
非常套路的题。
LCP 问题可以考虑二分+哈希,那么我们只需要判断两条有向链是否相等就好了,这个可以维护一个向上的哈希值和向下的哈希值计算出来,时间复杂度 (O(nlog^2 n))。
T2 CF505E Mr. Kitayuta vs. Bamboos (color{red}2color{blue}2color{green}2)
WC2021 讲课题。
最小化最大值考虑二分,同时考虑时间倒流,我们让所有竹子最开始高度都是二分出的 (mid),每一轮找到一个最小的 (k) 个数将它加 (p),如果 (k) 轮内没有小于 (0) 的数就表示这个 (mid) 是可行的。
每一轮找最小的数可以维护一下每个数变成 (0) 的时间,保存在大根堆里即可,时间复杂度 (O((n+mk)log nlog a))。
T3 CF506E Mr. Kitayuta's Gift (color{red}3color{blue}5color{green}5)
我们发现决定最终结果的是最后的串,与插入的方式无关,所以常规的 dp 无法去重。
于是我们考虑建立一个类似自动机的结构,又因为看到 (|s|leqslant 200,1leqslant nleqslant 10^9),所以又想到矩阵加速自动机上的 dp,那么我们的大致方向就已经确定了。
鸽了。
T4 CF512D Fox And Travelling (color{red}3color{blue}3color{green}2)
容易发现题意是一个类似拓扑排序的过程,进一步观察可以得到环上的所有点一定不能被选中,且去掉环之后每个连通块与环相邻的点一定是最后被选中的。(显然没有两个这样的点)
那么我们的问题转化为有/无根树的答案计数,我们算完之后将答案卷起来就可以了。而且实际上无根树的答案只需要钦定每个位置为根并去重就好了,去重只需要把选 (k) 个点的答案除以 (n-k) 即可。((n) 为树结点个数)
时间复杂度 (O(n^3))。
T5 CF516D Drazil and Morning Exercise (color{red}3color{blue}2color{green}1)
偏套路的二合一。
首先计算权值显然可以使用换根 dp 在 (O(n)) 内解决。
由于询问是问的 (max-minleqslant l) 这一经典模型,我们可以给所有点按照权值排序然后尺取法解决,时间复杂度 (O(nq))。
T6 CF516E Drazil and His Happy Friends (color{red}3color{blue}5color{green}3)
鸽了。
T7 CF521D Shop (color{red}2color{blue}1color{green}1)
简单题。
观察可以发现一定存在一种最优操作顺序满足先赋值,再加法,后乘法。
由于最后要最大化所有数的乘积,所以考虑直接把赋值和加法转化为乘法,这样我们只需要贪心选出前 (m) 个乘法操作即可。
给同一个位置的赋值显然只会选择最大的,然后我们就可以把赋值转化为加法了。加法操作显然可以从大到小执行,那么变化量可以直接计算出来。
最后选完最大的 (m) 个乘法操作输出方案的时候记得按照赋值、加法、乘法的顺序排个序,时间复杂度 (O(nlog n))。
T8 CF521E Cycling City (color{red}2color{blue}2color{green}1)
考虑三条完全不相交的路径实际上就是一个环中间一条弦,我们求出原图的 dfs 生成树,那么可以直接这样构造:
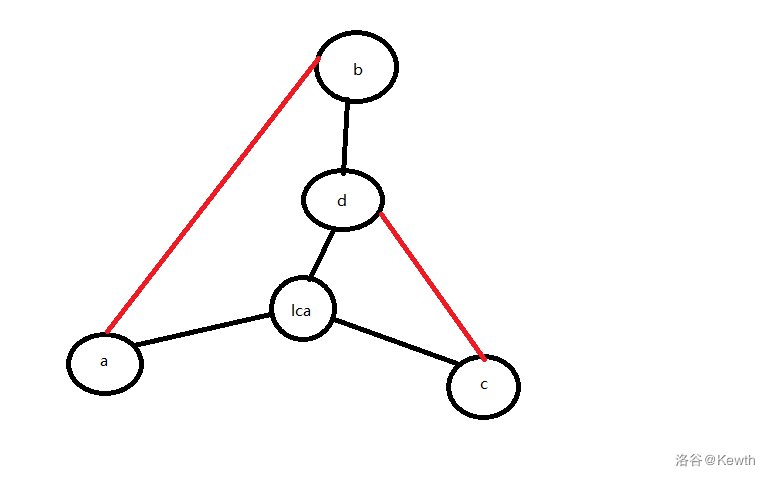
(蒯的洛谷题解图片)
那么我们每一条路径都暴力在树上覆盖,如果有重复覆盖的位置就直接输出就好了,时间复杂度 (O(n+m))。
T9 CF526F Pudding Monsters (color{red}2color{blue}3color{green}2)
每行每列一个棋子显然可以转化为一个长度为 (n) 的排列,那么恰好有 (k) 个棋子就等价于这个排列在这些位置的数字连续,即 (max-min+1=len)。
由于 (lenleqslant max-min+1),因此满足条件的排列都可以让 (max-min-len) 取到最小值 (-1)。
套路地固定右端点,可以用单调栈维护出每个后缀权值的 (max) 和 (min),再用一颗线段树维护每个左端点的答案,每次移动右端点就在更新单调栈的同时更新一下线段树,最后加上线段树最小值出现次数即可。(由于可以取长度为 (1) 的子段,所以(-1) 必定为最小值)
时间复杂度 (O(nlog n))。
T10 CF526G Spiders Evil Plan (color{red}3color{blue}4color{green}3)
鸽了。
T30 CF575I Robots protection (color{red}3color{blue}2color{green}2)
首先容易发现直角三角形的方向并不重要,我们旋转坐标系就可以等价,于是我们只需要考虑一种情况。
我们考虑直角三角形实际上是要求点满足 (xgeqslant a,ygeqslant b,x+yleqslant a+b+len),我们带上时间就是一个四维偏序,三个 (log) 貌似过不了。
对 (xgeqslant a) 以及 (ygeqslant b) 进行容斥,可以发现总方案数减 (x<a) 减 (y<b) 加 (x<a,y<b) 只有最后一个是四维偏序,而由于 (x+y<a+bleqslant a+b+len),所以可以去掉一维变成三维偏序。
用二维树状数组维护即可,时间复杂度 (O(nlog^2 n))。