Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
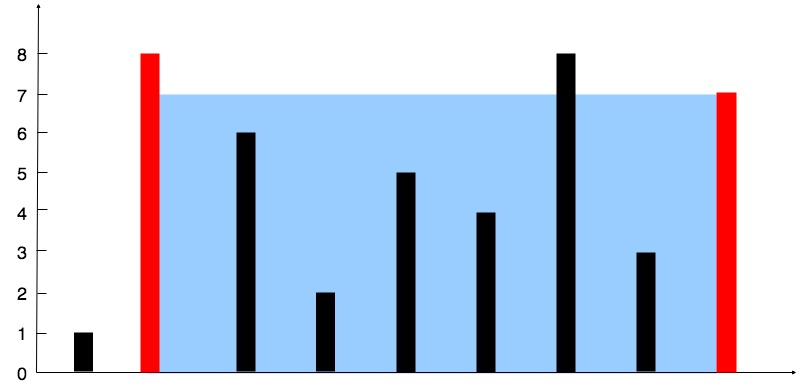
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example:
Input: [1,8,6,2,5,4,8,3,7]
Output: 49
很快就写了一个暴力搜索的方法,不过很显然不是最优解:
class Solution {
public:
int maxArea(vector<int>& height) {
//
int vol = 0;
//
if(height.size()<2) return vol;
else;
//
for(int i=0;i<height.size();i++)
{
for(int j=i;j<height.size();j++)
{
int curr_height = (height[i] >= height[j]) ? height[j]:height[i];
int curr_vol = (j-i)*curr_height;
if(curr_vol > vol) vol = curr_vol;
}
}
return vol;
}
};
后来参考了一下这道题的简易算法,速度当真快了不少。其核心思想是,水桶所能承水的高度受到最低木板的限制,而最低木板想要实现最大容量需要最长的区间长度。在实现算法时,我们从边缘向中间逼近,利用较短的木板计算当前区间的最大容水量,并且不断迭代最短木板位置向中心靠近,由此求解最大容水量。
class Solution {
public:
int maxArea(vector<int>& height) {
//
int vol = 0;
//
if(height.size()<2) return vol;
else;
//cool algorithms
int s =0;
int t = height.size()-1;
while(s<t)
{
int curr_height = (height[s] >= height[t])? height[t]:height[s];
int curr_vol = curr_height * (t-s);
if(curr_vol > vol) vol = curr_vol;
if(height[s]>=height[t]) t--;
else s++;
}
return vol;
}
};