一、贝叶斯简介
贝叶斯(约1701-1761) Thomas Bayes,英国数学家,贝叶斯方法源于他生前为解决一个“逆概”问题写的一篇文章,生不逢时,死后它的作品才被世人认可。

贝叶斯要解决的问题:
正向概率:假设袋子里面有N个白球,M个黑球,你伸手进去摸一把,摸出黑球的概率是多大?
逆向概率:如果我们事先并不知道袋子里面黑白球的比例,而是闭着眼睛摸出一个(或好几个)球,观察这些取出来的球的颜色之后,那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测。
现实世界有很多问题本身就是不确定的(比如上面的逆向概率,不确定球的个数),而人类的观察能力是有局限性的,由于我们日常所观察到的只是事物表面上的结果(比如上面的逆向概率,观察取出来的球的颜色),因此我们需要提供一个猜测来得到袋子里面球的比例。
二、贝叶斯推导过程
首先引入一个栗子,假设在一个学校里面男生的概率和女生的概率分别是60%和40%,男生总是穿长裤,女生则一半穿长裤一半穿裙子。
正向概率:随机选取一个学生,他(她)穿长裤的概率和穿裙子的概率是多大?这个比例的计算就比较简单了。
逆向概率:迎面走来一个穿长裤的学生,你只看得见他(她)穿的是否长裤,而无法确定他(她)的性别,你能够推断出他(她)是女生的概率是多大吗?这就是我们要解决的问题。

假设学校里面人的总数是 U 个,那么我们可以得到穿长裤的男生的概率为:U * P(Boy) * P(Pants|Boy),P(Boy) 是男生的概率 = 60%,P(Pants|Boy) 是条件概率,即在 Boy 这个条件下穿长裤的概率是多大,这里是 100% ,因为所有男生都穿长裤。同理可以得到穿长裤的女生的概率为: U * P(Girl) * P(Pants|Girl)。
那么接下来求解穿长裤的人是女生的概率。可以首先求出穿长裤总数:U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)。那接下来求解穿长裤的人是女生的概率(女生穿长裤的总数/穿长裤的总数)就简单了吧。P(Girl|Pants) = U * P(Girl) * P(Pants|Girl)/穿长裤总数。将穿长裤总数代入得到 P(Girl|Pants) = U * P(Girl) * P(Pants|Girl) / [U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)]
这里引发了一个新的问题,就是在问题的最开始,我们假设了一个无关变量U,很显然,我们并不知道U的具体值,那岂不是说明穿长裤的人是女生的概率还是无法计算。那我们再仔细看看结果到底与总人数有没有关系。P(Girl|Pants) = U * P(Girl) * P(Pants|Girl) / [U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl),容易发现这里校园内人的总数是无关的,可以消去,那么最终结果就是P(Girl|Pants) = P(Girl) * P(Pants|Girl) / [P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)]
然后进行进一步的化简:
P(Girl|Pants) = P(Girl) * P(Pants|Girl) / [P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)],因为分母代表穿长裤的男生的概率+穿长裤的女生的概率,那这个分母实际上代表的就是穿长裤的概率P(Pants)。
于是我们就可以得出贝叶斯公式
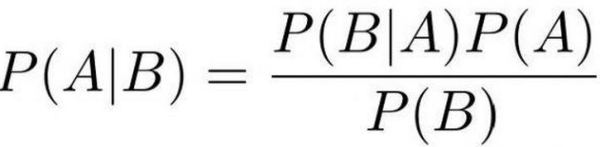
在实际情况下,在B的条件下A发生的概率其实并不太好求,于是我们可以通过贝叶斯公式转换为求解在A的条件B发生的概率(这个一般都是比较好求的),而A发生的概率和B发生的概率一般都是已知的。
三、拼写纠正实例:
问题是我们看到用户输入了一个不在字典中的单词,我们需要去猜测:“这个家伙到底真正想输入的单词是什么呢?比如说用户想输入单词the或者than,而实际上用户却输入tha。我们的目的就是得到用户真实想输入的单词的一个概率。转换为概率就是:P(我们猜测他想输入的单词 | 他实际输入的单词)
假设用户实际输入的单词记为D(D 代表 Data ),实际上我们也不知道用户真实想输入的单词到底是什么,我们可与做出如下猜测,h代表真实的单词。猜测1:P(h1 | D),猜测2:P(h2 | D),猜测3:P(h3 | D) 。。。那么统一下来就是:P(h | D)。实际上P(h | D)并不太好求, P(D | h)相对而言就比较好求一点,通过贝叶斯公式可得:P(h | D) = P(h) * P(D | h) / P(D)
假设在一个语料库中,假设总共单词数目有10000个,the这个单词出现了5000次,than这个单词出现了1000次,假设h1代表the这个单词,h2代表than这个单词,那么P(h1)=5000/10000,P(h2)=1000/10000。P(D | h1)代表用户在想输入单词the的情况下实际却输成单词tha的概率,也就是输错的概率。
用户实际输入的单词记为 D (D 代表 Data,即观测数据),对于不同的具体猜测 h1 h2 h3 .. ,P(D) 都是一样的,所以在比较P(h1 | D) 和 P(h2 | D) 的时候我们可以忽略这个常数,于是我们可以得到 P(h | D) ∝ P(h) * P(D | h)。对于给定观测数据D,一个猜测是好是坏,取决于“这个猜测本身独立的可能性大小(即先验概率,P(h))”和“这个猜测生成我们观测到的数据的可能性大小(P(D | h))“。
比如用户输入tlp ,那到底是 top 还是 tip ?这个时候,当最大似然法不能作出决定性的判断时,先验概率就可以插手进来给出指示——“既然你无法决定,那么我告诉你,一般来说 top 出现的程度要高许多,所以更可能他想输入的是 top ”
朴素贝叶斯:在前面的回归算法我们假设误差服从独立同分布,那在贝叶斯算法中假设P(D | h)也是服从独立同分布的,就是P(D | h)相互之间互不影响,那么这个算法就叫做朴素贝叶斯算法。
四、垃圾邮件过滤实例
模型比较理论
最大似然估计:最符合观测数据的(即 P(D | h) 最大)最有优势。掷一个硬币,观察到的是“正”,根据最大似然估计的精神,我们应该猜测这枚硬币掷出“正”的概率是 1,因为这个才是能最大化 P(D | h)的那个猜测。
奥卡姆剃刀: P(h)较大即先验概率较大的模型有较大的优势。如果平面上有 N 个点,近似构成一条直线,但绝不精确地位于一条直线上。这时我们既可以用直线来拟合(模型1),也可以用二阶多项式(模型2)拟合,也可以用三阶多项式(模型3),特别地,用 N-1 阶多项式便能够保证肯定能完美通过 N 个数据点。那么,这些可能的模型之中到底哪个是最靠谱的呢?奥卡姆剃刀:越是高阶的多项式越是不常见,所以最常见的就是用直线来拟合,奥卡姆剃刀的追求就是在实际中什么越常见,那么结果就越好。
垃圾邮件过滤实例:
问题:给定一封邮件,判定它是否属于垃圾邮件。D 来表示这封邮件,注意 D 由 N 个单词组成。我们用 h+ 来表示垃圾邮件,h- 表示正常邮件。
邮件一般要进行分类吧,分为垃圾邮件和正常邮件,我们就可以通过贝叶斯算法来计算垃圾邮件的正常邮件的概率。垃圾邮件:P(h+|D) = P(h+) * P(D|h+) / P(D),正常邮件:P(h- |D) = P(h- ) * P(D|h- ) / P(D)
先验概率:P(h+) 和 P(h-) 这两个先验概率都是很容易求出来的,只需要计算一个邮件库里面垃圾邮件和正常邮件的比例就行了。
D 里面含有 N 个单词 d1, d2, d3,P(D|h+) = P(d1,d2,..,dn|h+),P(d1,d2,..,dn|h+) 就是说在垃圾邮件当中出现跟我们目前这封邮件一模一样的一封邮件的概率是多大!这也太精确了吧,在实际中判定一封邮件是垃圾邮件肯定没有这么精确吧,只要大致相同就行了吧,于是我们把P(d1,d2,..,dn|h+) 扩展为: P(d1|h+) * P(d2|d1, h+) * P(d3|d2,d1,h+) * ..
P(d1|h+) * P(d2|d1, h+) * P(d3|d2,d1, h+) * ..,对于这个式子来说,计算过程有点太复杂了,我们可以将它转换为一个朴素贝叶斯问题,假设 di 与 di-1 是完全条件无关的(朴素贝叶斯假设特征之间是独立,互不影响)于是我们可以把这个式子简化为 P(d1|h+) * P(d2|h+) * P(d3|h+) * ..,对于P(d1|h+) * P(d2|h+) * P(d3|h+) * ..,只要统计 di 这个单词在垃圾邮件中出现的频率即可。