二分图问题

一、问题描述

　　给定一个具有n个顶点的图，要给图上每个顶点染色并且要使相邻的顶点的颜色不同，问是否最多用2种颜色进行染色？没有重边和自环。把相邻顶点染成不同颜色的问题叫做图的着色问题。对图进行染色所需的最小颜色数，称为最小着色数。最小着色数为2的图称为二分图，如下图所示就是一个二分图。下面代码是用来判断是否二分图。

　　

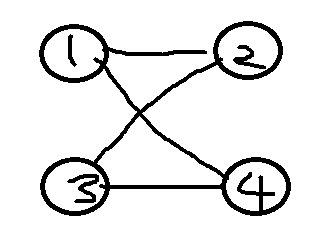
二、思路

　　直接DFS即可，要注意代码里面的一些细节。

三、代码

public class 图的着色_二分图 {
    static boolean dfs(MyNode node, int c) {
        node.color = c;// 同时标记已访问和具体颜色
        for (int i = 0; i < node.size(); i++) {// 遍历所有neighbor
            MyNode neighbor = (MyNode) node.getNeighbor(i);// 具体的neighbor
            // 如果相邻节点颜色一样，返回false
            if (neighbor.color == c)
                return false;
            // 没有被染色，就染不同颜色进行递归
            if (neighbor.color == 0) {
                boolean res = dfs(neighbor, -c);
                if (!res)
                    return false;
            }
        }
        return true;
    }

    public static void main(String[] args) {
        // 下面的数据表示的就是上面的图
        MyNode n1 = new MyNode(1);
        MyNode n2 = new MyNode(2);
        MyNode n3 = new MyNode(3);
        MyNode n4 = new MyNode(4);

        n1.add(n2);
        n1.add(n4);

        n2.add(n1);
        n2.add(n3);

        n3.add(n2);
        n3.add(n4);

        n4.add(n1);
        n4.add(n3);

        // 任意顶点都可以
        System.out.println(dfs(n1, 1));  // 输出 true
    }

    // GraphNode_AL这个类在前面博客  邻接表表示图
    static class MyNode extends GraphNode_AL {
        int color;

        public MyNode(int val) {
            super(val);
        }

        public MyNode(int val, int color) {
            super(val);
            this.color = color;
        }
    }
}