一、定义:
没有圈的有向图,叫做DAG(Directed Acyclic Graph,有向无环图)

拓扑排序定义:将DAG中的顶点以线性方式进行排序。即对于任何自顶点u到顶点v的有向边u->v,在最后的排序结果中,顶点u总是在顶点v的前面。这样的排序结果,称为拓扑序。有环图,不存在拓扑排序。
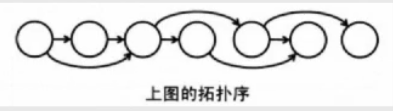
二、拓扑排序具体的应用
三、代码实现
这份代码还有判断是否有环的功能。
1 /*具有检测是否有环的功能*/ 2 public class 图的dfs_拓扑排序 { 3 // 顶点数 4 static final int n = 4; 5 // 顶点内容 6 static String[] v = { "a", "b", "c", "d" }; 7 // 有向图的邻接矩阵表示法 8 static int[][] graph = { { 0, 1, 0, 0 }, { 0, 0, 0, 0 }, { 0, 1, 0, 0 }, { 0, 0, 1, 0 }, }; 9 // 标记顶点访问状态,1:已经访问并返回,0:从未被方位,-1:正在递归访问还未退出 10 static int[] vis = new int[n]; 11 // 拓扑排序结果 12 static int[] topo = new int[n]; 13 // 标记topo数组的哪一位被改写 14 static int t = n; 15 16 public static void main(String[] args) { 17 // 对所有顶点进行迭代 18 for (int i = 0; i < n; i++) { 19 // 如果被访问,则跳过 20 if (vis[i] == 1) 21 continue; 22 23 boolean bool = dfs(i);// 是否有拓扑序 24 if (!bool) { 25 System.out.println(false); 26 return; 27 } 28 } 29 for (int i = 0; i < n; i++) { 30 System.out.println(v[topo[i]]); // 输出 d c a b 31 } 32 } 33 34 private static boolean dfs(int i) { 35 vis[i] = -1; 36 //遍历所有顶点 37 for (int j = 0; j < n; j++) { 38 if (graph[i][j] > 0) {//当前关注顶点i到顶点j有出度 39 //此处,关于j顶点的递归还没有退出,前驱的状态是-1,后继的状态也是-1,说明在此次递归的链路上早就路过了j,现在是第二次路过j, 40 // 一次递归链路两次经过j,只有一种情况,形成了环 41 if (vis[j] < 0) return false; 42 //j没被访问过,执行递归 43 if (vis[j] == 0 && dfs(j) == false) return false; 44 } 45 } 46 //整个递归是按照出度方向来的,所以上面的循环+递归走到尽头时,i没有出度,没有出度的点可以认为是最大的点(之一) 47 topo[--t] = i; 48 vis[i] = 1; 49 return true; 50 } 51 }