算法复杂度的评估以及常用函数的复杂度计算

一、评估算法复杂度

　　

　　举例：

　　　　算法复杂度为O(n)：

　　　　　　

　　　　算法复杂度为O(n²)：

　　　　　　

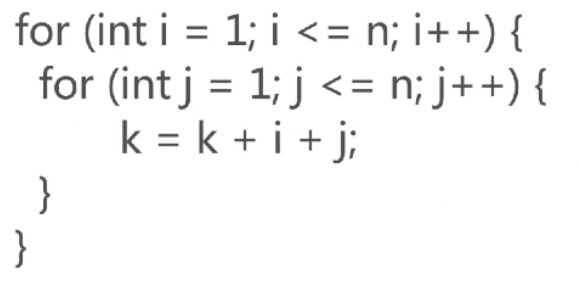
　　　　算法复杂度为O(1+2+...+n) ---> O(n²)：

　　　　　　

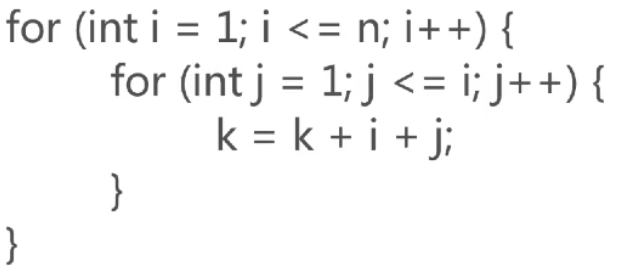
　　　　算法复杂度为O(lgN):

 　　　　　　

　　　　算法复杂度为O(1):

　　　　　　高斯解决1+2+3+....+100的办法 （1+100)*50  常数阶算法

二、常见函数的复杂度计算

　　横轴代表数据规模，纵轴代表所花时间，这个图很重要，希望大家记住。

　　

　　

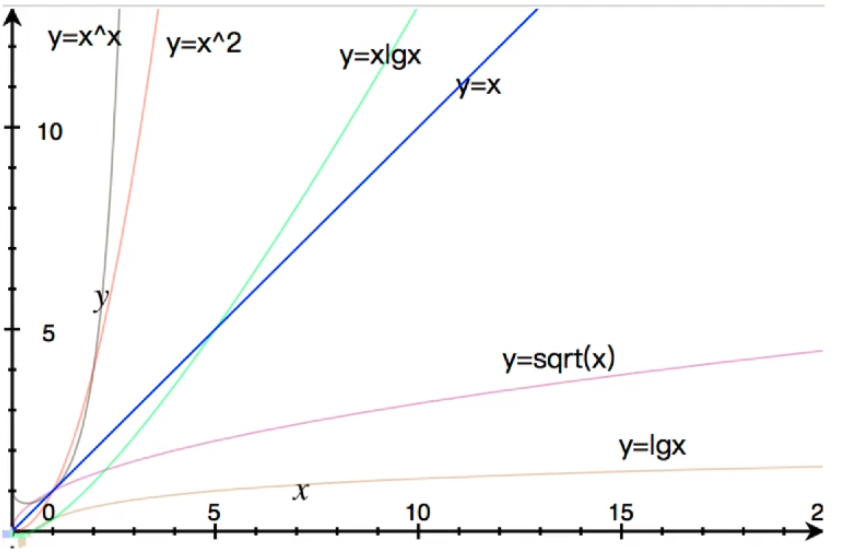
 　　直观地看算法复杂度与处理规模与所花时间的关系  100000000次运算大概1秒

　　

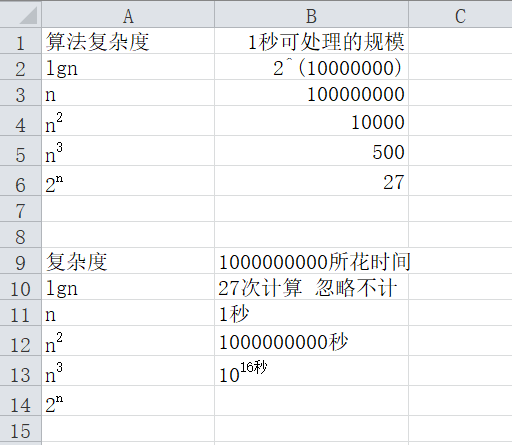
　　所以在日常算法的设计中，需要尽量把算法复杂度优化到接近成O(lgN)。

三、顺序查找与二分查找的性能对比

　　代码： 

public class Contrast {

    public static void main(String[] args) {
        
        int []x = new int[10000*10000];
        for (int i = 0; i < x.length; i++) {
            x[i] = i+1;
        }
        
        int target = 10000*10000;
        
        long now = System.currentTimeMillis();  // 统计当前时间的方法
        int index = binarySearch(x, 0, x.length-1, target);
        System.out.println("二分查找所需时间:"+(System.currentTimeMillis()-now)+"ms");
        System.out.println(target+"所在位置为："+index);
        
        now = System.currentTimeMillis();
        index = search(x, target);
        System.out.println("顺序查找所需时间:"+(System.currentTimeMillis()-now)+"ms");
    }
    
    /**
     * 二分查找  非递归
     * @param arr
     * @param low
     * @param high
     * @param key
     * @return
     */
    static int binarySearch(int arr[],int low,int high,int key){
        while(low<=high){
            int mid = low + ((high-low) >> 1);   //  (high+low) >>> 1  防止溢出，移位更加高效，同时，每次循环都需要更新
            int midVal = arr[mid];
            
            if (midVal<key) {
                low = mid +1;
            }else if (midVal>key) {
                high = mid - 1;
            }else {
                return mid;    // key found
            }
        }
        return -(low + 1);   // key not found
    }

    /**
     * 顺序查找
     */
    static int search(int arr[],int key){
        for (int i = 0; i < arr.length; i++) {
            if (arr[i]==key) {
                return i;
            }
        }
        return -1;
    }
}

　　结果：

　　　　

　　结论：二分查找时间为0ms，时间几乎可以忽略不计，可以发现这两种查找算法的时间相差很大，所以O(lgn)与O(n)的性能差别很大，

四、基础排序算法的性能对比

　　二的幂表

　　

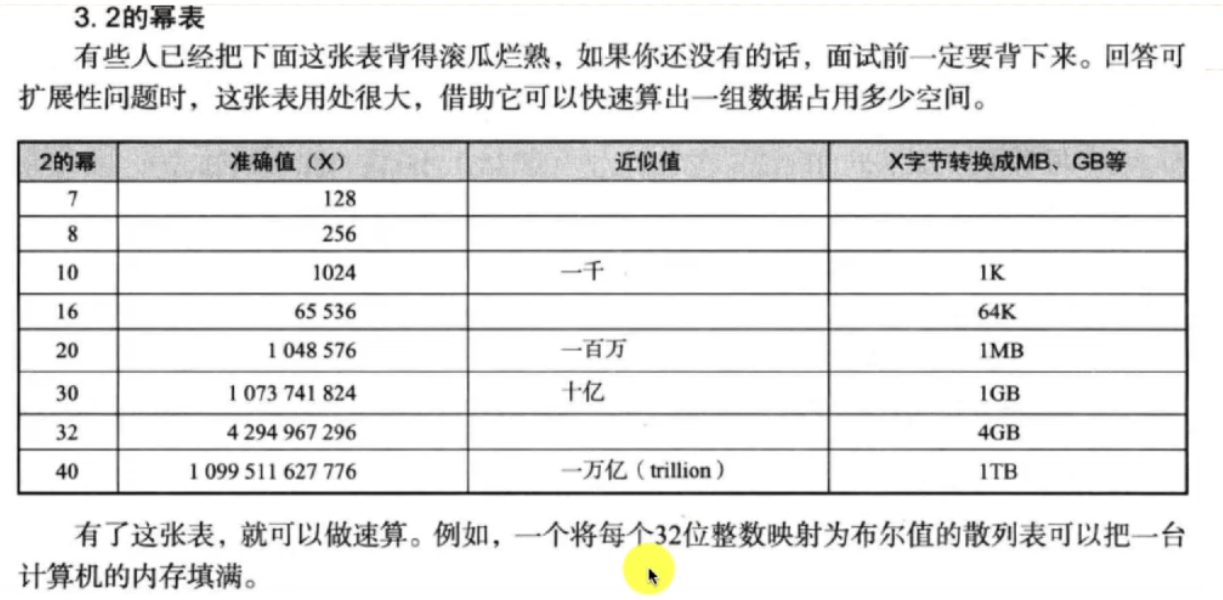
　　冒泡、插入、选择排序  这些排序算法的时间复杂度就是O(n²)

　　Arrays.sort() 采用的快速排序，时间复杂度是O(nlgn)  所以有时采用这个方法排序还比上面的排序算法好用。

四、递归算法的性能分析　

　　1、子问题的规模下降        T(n/2) 代表每一层丢一半     T(n-1)代表下降一层
　　2、子问题的答案的处理消耗的时间       每一层消耗的时间       O(1)代表每一层消耗常数时间        O(n)代表每一层消耗线性时间
　　写出类似下面的式子。
　　T(n) = T(n-1) +O(1)