DFS
深度优先搜索
通过搜索得到一棵树形图
策略:只要能发现没走过的点,就走到它。有多个点可走就随便挑一个,如果无路可走就回退,再看有没有没走过的点可走。
在图上寻找路径【少数可用最短路解决】:最短路不能解决路径有顺序的,也就是如果路径的边权与之前经过的点火这路有关,那就只能深搜
解决递归形式的问题
有后效性的选择问题
组合问题
状态可能很多,因此数据范围一般较小
1、状态表示
2、剪枝
剪枝的方法:
最优答案剪枝
记忆化剪枝
可行性剪枝
……
1、洪水[ 1s 32M ]

题解
数据范围小,搜索




2、辛苦的老园丁 [1s 128M] [1s 32M]

题解
建反图找团(简单地说,团是G的一个完全子图)
原来输入建图是标记的两点之间不能有连边,建反图之后,连边的就是可以连通的
剪枝:
1.如果一个点与点i当前没有连边,那么之后永远都不会连边,那么就可以把点i从最大团候选中删掉
2.利用可行点剪枝 sum+tot<=ans ,舍弃
3.利用当前答案剪枝ans(2)+tot<=ans
(tot 是团不断累加的权值,sum是序列里面剩下的所有东西的权值和
若sum+tot<=ans ,舍弃)
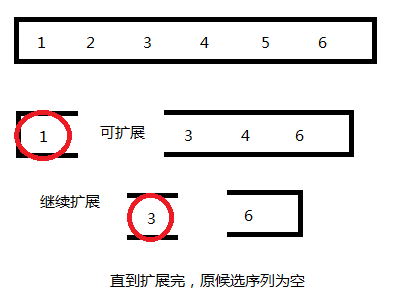
可能组成最大团的点一开始在一个序列里
取出一个点,不断扩展,当序列为空,扩展完了
首先拿出1 ,那么序列被更新为与1相连的点
不断扩展,直到队列为空,找完团了




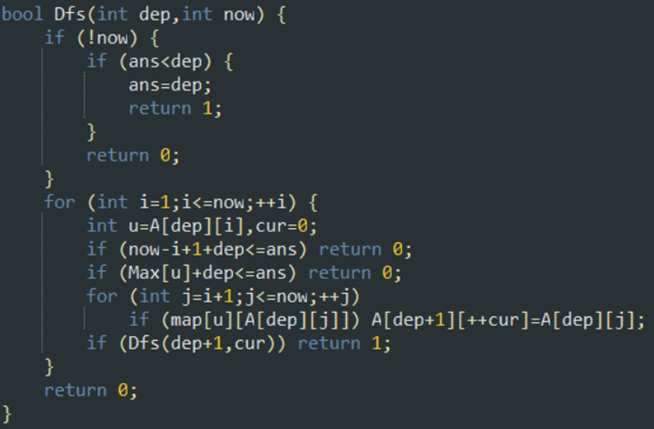
 --->sum+tot<=ans
--->sum+tot<=ans
最大团主函数:

为什么找最大团而不是最大独立集呢??

3、生日蛋糕 [ 1s 10M]

题解


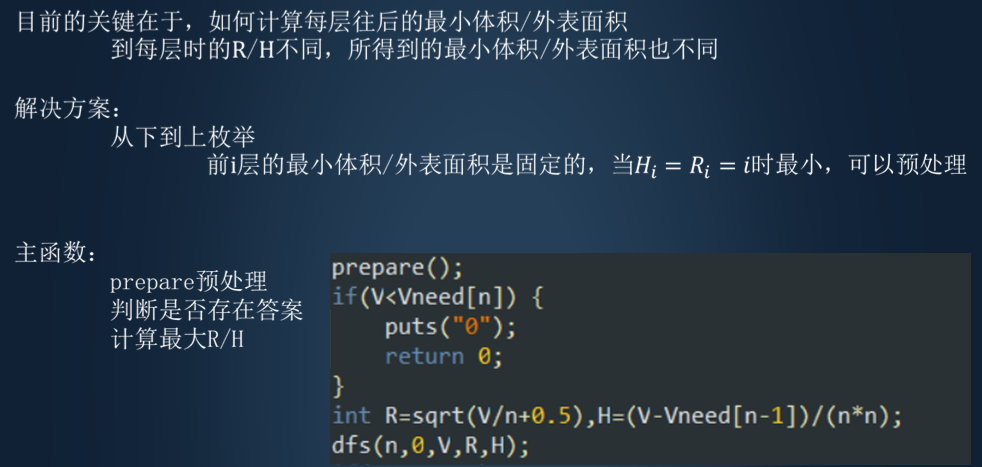

4、靶形数独[2s128M]

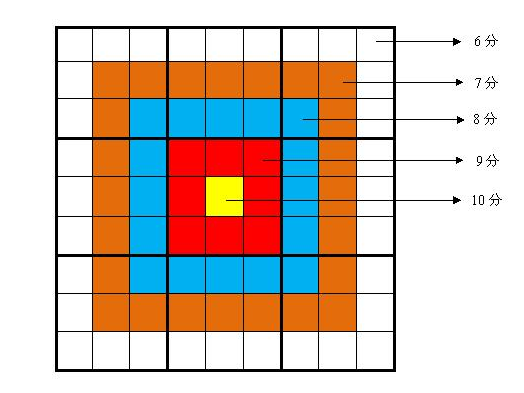
题解

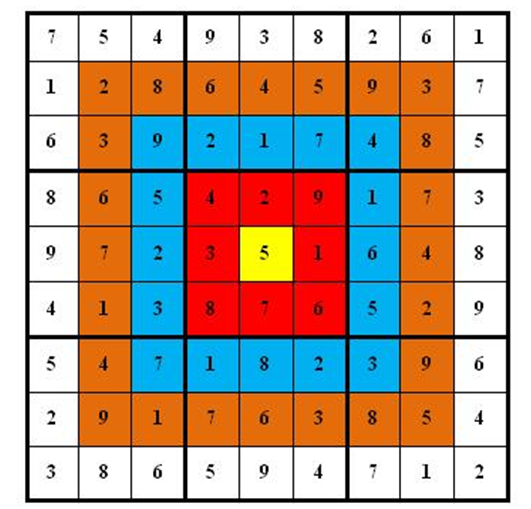

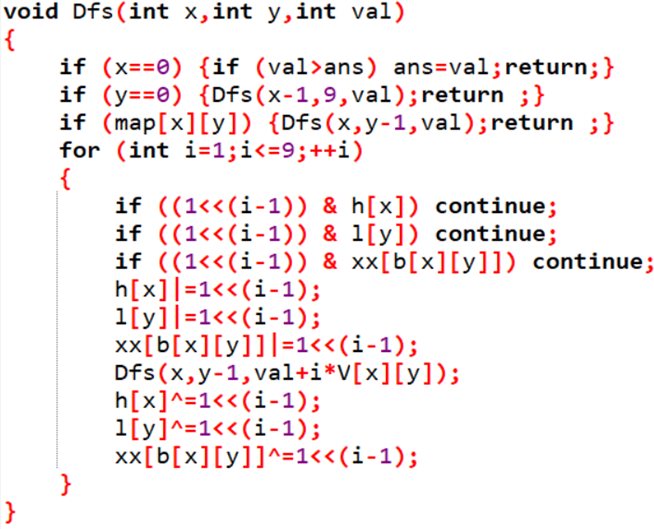
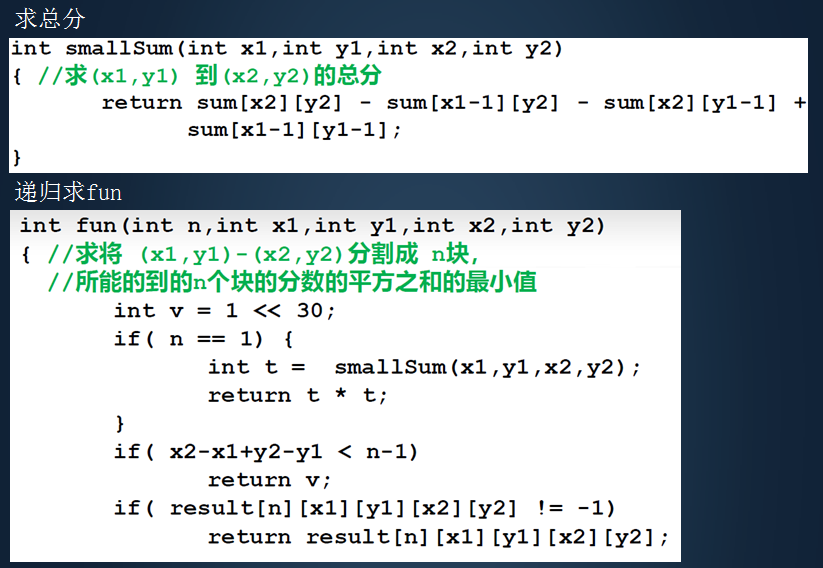
5、棋盘分割 [1s 16M]

题解



BFS
宽度优先搜索

1、密室逃脱 [ 1s 64M ]

题解

queue<pair<int,int> > Q; int FindPath(pair<int,int> b,pair<int,int> e) { for (int i=0;i<n;++i) for (int j=0;j<m;++j) dis[i][j]=1e9+10; Q.push(b); dis[b.first][b.second]=0; while (!Q.empty()) { pair<int,int> u=Q.front(); Q.pop(); int x=u.first,y=u.second; for (int i=0;i<4;++i) { int tx=x+dx[i],ty=y+dy[i]; if (CoordValid(tx,ty) && mp[tx][ty]!=0 && dis[tx][ty]>dis[x][y]+1) { dis[tx][ty]=dis[x][y]+1; Q.push(make_pair(tx,ty)); } } } return dis[e.first][e.second]; }
2、Prime Path[ 1s 64M ]

题解
记录当前素数的值
每次选择一个位置,将其该改为另一个数
检查新的数是否是素数
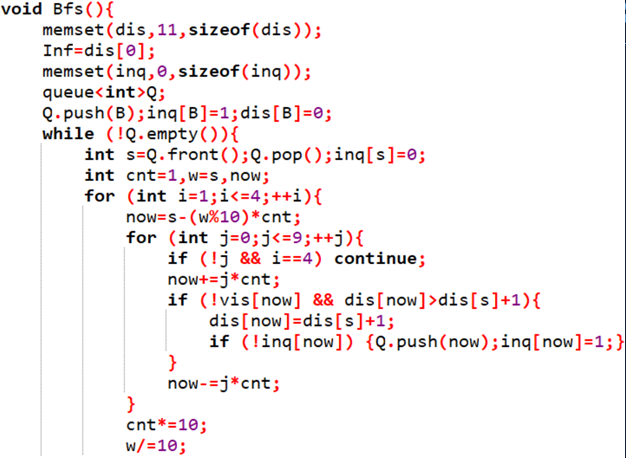

3、拯救行动 [ 1s 64M ]

题解

(Python源码)
BFS部分

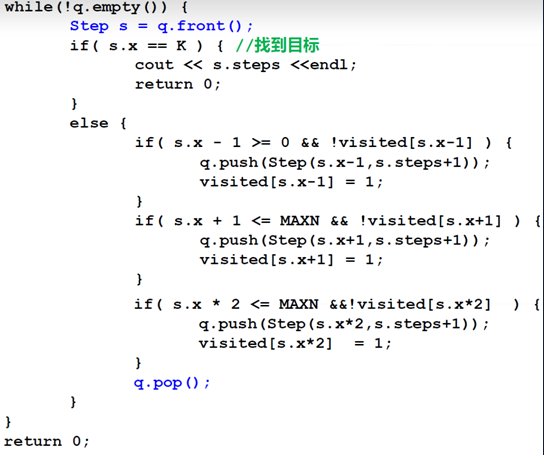
4、抓住那头牛 [ 1s 64M ]

题解

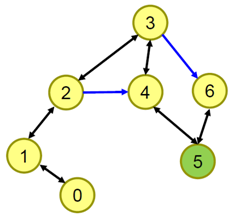
BFS
双向BFS(DBFS)

对比BFS和DFS
广搜一般用于状态表示比较简单求最优策略的问题l
优点:是一种完备策略,即只要问题有解,它就一定可以找到解。并且,广度优先搜索找到的解,还 一定是路径最短的解。
缺点:盲目性较大,尤其是当目标节点距初始节点较远时,将产生许多无用的节点,因此其搜索效率较低。需要保存所有扩展出的状态,占用的空间大
深搜几乎可以用于任何问题
只需要保存 从起始状态到当前状态路径上的节点
根据题目要求凭借自己的经验和对两个搜索的熟练程度做出选择
枚举
1、苹果消消乐 [ 1s 64MB]
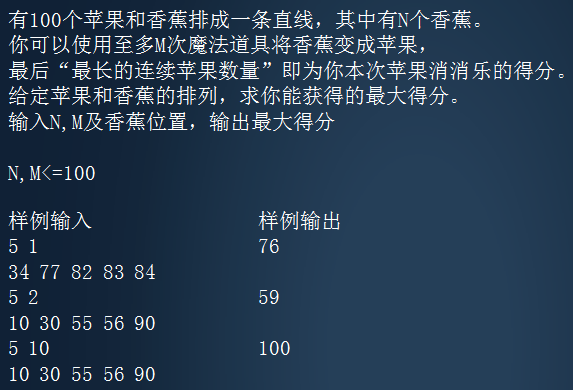
题解
选择连续的香蕉时最优
枚举选择的香蕉起始位置,计算答案

2、Matrix [ 2s 512MB ]

题解



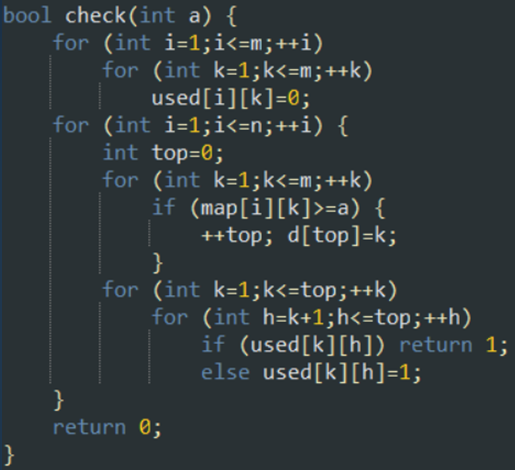
Check函数:
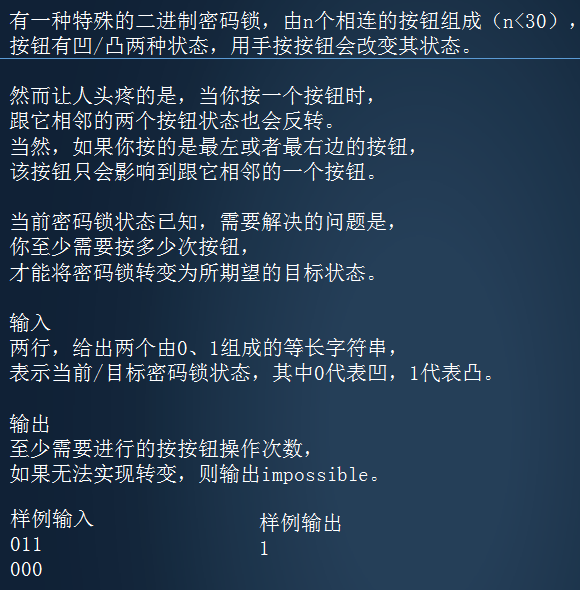
4、特殊密码锁[ 1s 64M ]
题解
1、 已知,在首位状态固定后,后续的操作是确定的。
2、 只需要枚举首位是否按即可。

5、恼人的青蛙[ 2s 64M ]
题解
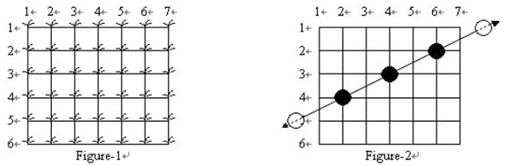
①不是一条行走路径:只有两棵被踩踏的水稻;
②是一条行走路径,但不包括(2,6)上的水道;
③不是一条行走路径:虽然有3棵被踩踏的水稻,
但这三棵水稻之间的距离间隔不相等。
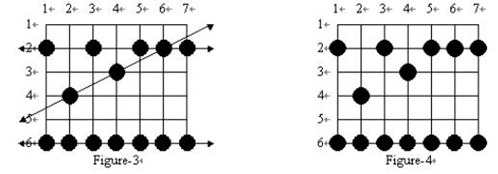
例如,图4的答案是7,
因为第6行上全部水稻恰好构成一条青蛙行走路径。

题解


枚举主函数


枚举得到最大步数

重识枚举
枚举:基于已知信息的猜测,从可能的答案集合中枚举并验证
验证复杂度尽可能小
枚举范围尽可能小(利用条件缩小枚举空间)
选择合理的枚举顺序(正序,倒序)
枚举什么?
怎么枚举?
怎么减少枚举?
二进制枚举
5、熄灯问题[ 1s 64M ]


题解


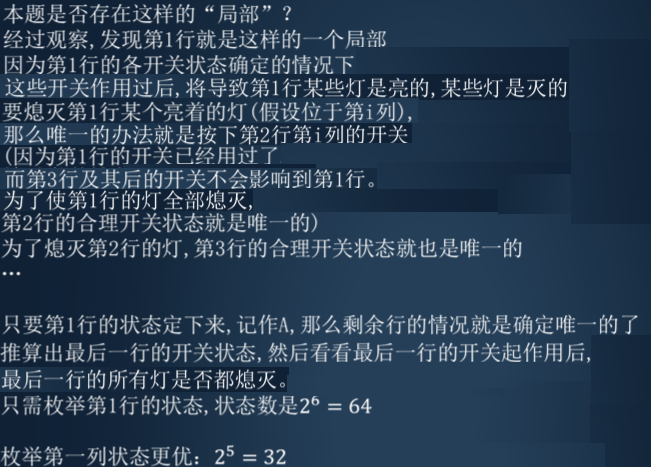
二进制枚举

推导最后一行

二进制枚举
二进制的枚举一般用以枚举集合
对集合的枚举涉及到不同的集合内部元素的选择
枚举子集
for(int S1=S;S1!=0;S1=(S1-1)&S){
S2=S^S1;
}
