DP&图论 DAY 5 下午
树链剖分

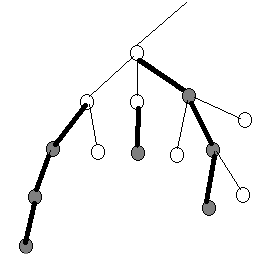

每一条边要么属于重链要么轻边

证明: https://www.cnblogs.com/sagitta/p/5660749.html
轻边重链都是交替走的(此处重链可以走若干条边)
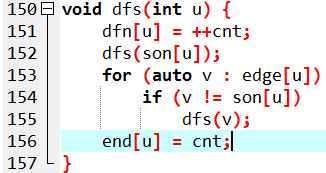
1.dfs1 统计子树大小,确定重儿子
2.dfs2 找重链 重链,子树,分别是连续的一段
每个结点属于一个重链


ta < tb
a 跳到 ta 的父节点
logn 级别
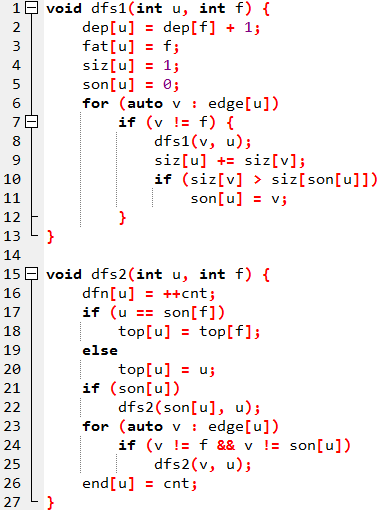

将树序列化

SPOJ QTREE Query on a tree

Solution
树链剖分 + 线段树维护区间最大值
BFS 树链剖分 边权摊到点上
BZOJ 1036 树的统计

Solution
BZOJ 4034
有一棵点数为 N 的树,以点 1 为根,且树点有权。然后有 M
个操作,分为三种:
1. 把某个节点 x 的点权增加 a 。
2. 把某个节点 x 为根的子树中所有点的点权都增加 a 。
3. 询问某个节点 x 到根的路径中所有点的点权和。
Solution

单点加
区间修改
区间查询
BZOJ 2243 染色

Solution

同时维护区间左右端点颜色

若相同,左右颜色段数相加-1
不相同,直接加起来


BZOJ 2238 MST

Solution
1.对于m-n+1条非最小生成树上的边,不会对原来的最小生成树产生影响,直接出结果
2.对于最小生成树上的边,用别的来替代


强连通分量

缩点

Tarjan 算法


// Tarjan void tarjan(int u) { dfn[u] = low[u] = ++tim; stk[++top] = u; for (int i = hd[u], v; i; i = nt[i]) if (v = to[i], !scc[v]) { if (!dfn[v])tarjan(v), low[u] = min(low[u], low[v]); else low[u] = min(low[u], dfn[v]); } if (dfn[u] == low[u]) { ++cnt; do { scc[stk[top]] = cnt; } while (stk[top--] != u); } }
BZOJ 2208 连通数
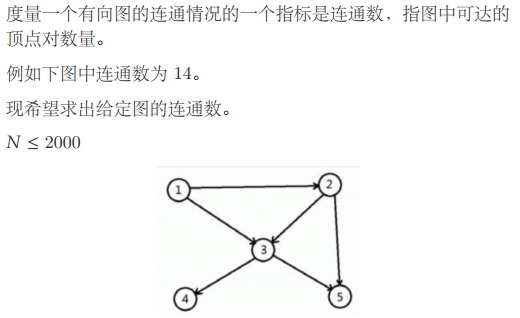
14: 1-2 , 1-3 , 1-4 , 1-5 , 2-3 , 2-5 , 2-4 , 3-5 , 3-4
Solution
bitset

bitset<100000>a;长度为1e5的二进制数

可以数组O(1)查询,赋值

支持位运算
a.count( ) 统计 a 里面有多少位为 1
POJ 2186 Popular Cows


POJ 1236 Network of Schools

Solution
