NOIp膜你题 Day2
duliu 出题人:ZAY


题解
这就是一道组合数问题鸭!!! 可是泥为什么没有推出式子!!
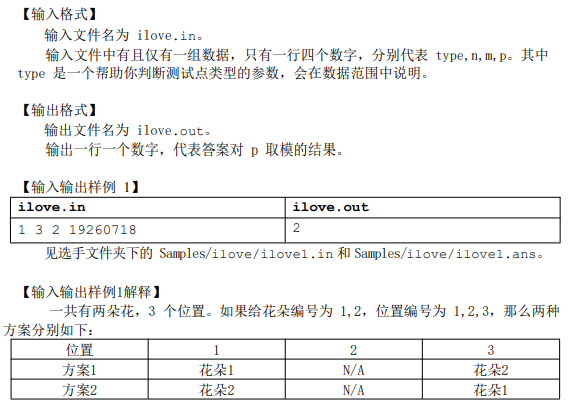
首先我们知道的是 m 盆花都要摆上,然后他们的顺序不定(主人公忘记了)
所以初步得到一个排列数 P( m,m ) , 即 Pmm
那么我们就还剩下 n-m 个空位置,这些空位置都是不可以放花的,于是我们逆向思维一下:
n-m 个位置不放花,也就是可以在这些位置周围插空放花,把这些位置隔开,那么就可以把m盆花放到 n-m+1 个空里,由于这是对于空位置来说的,没有顺序可言,每个都是一毛一样的,所以得到一个组合数 C(n-m+1 , m) , 即 Cn-m+1m
所以 ans = P( m,m ) * C( n-m+1 , m )
= m! * (n-m+1)! / [ m! * (n-m+1 - m)! ]
化简一下就是下面
=(n-m+1)*(n-m+1-1)*......*(n-2m+2)
注意
ans 要开 long long , 试过毒了,数据不开 long long 会炸
代码
#include<bits/stdc++.h> using namespace std; int type,n,m,p; long long ans=1; int main() { freopen("ilove.in","r",stdin); freopen("ilove.out","w",stdout); scanf("%d%d%d%d",&type,&n,&m,&p); if(n==1&&m==1) { printf("1 "); return 0; } int a=n-m+1,b=n-m-m+2; for(int i=a;i>=b;i--) ans=(ans%p*i%p)%p; printf("%ld ",ans); return 0; }
看看出题人的题解
一般这种数数题,也就是求方案数,有两种解决方案:DP&组合数学
1.DP

2.组合数学

Ps:插空法就是我上面题解里面提到的



题解
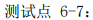
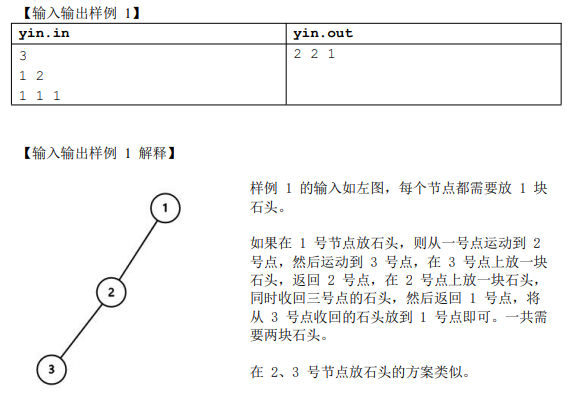
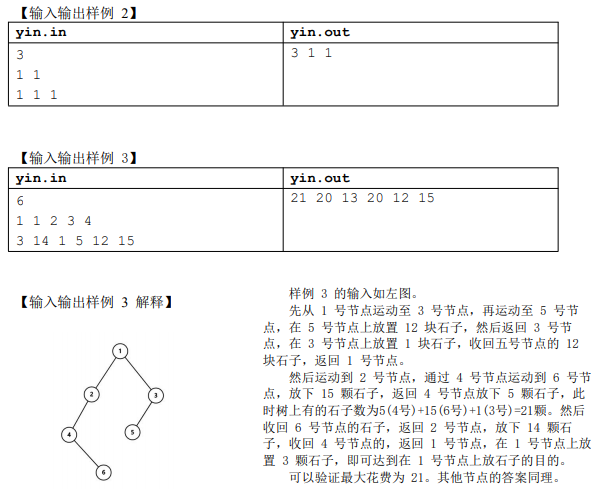
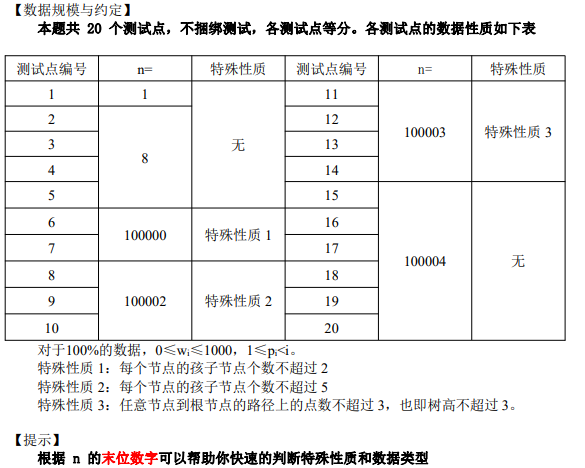
注意到根据题目规定的走法,在进入一个节点以后,必须遍历完它的整个子树, 否则一旦离开这个节点,再也无法进入这棵子树,从而导致该节点的某个孩子没能放 上石子,导致这个节点不能放上石子。
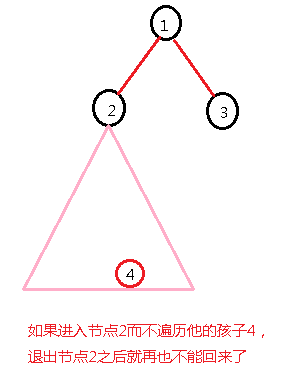
同时又有每个节点放上石子以后,它的子树的 石子可以全部取回。设在节点 u 放石子需要有 ansu 个石子,则放完 u 以后可以取回 ansu-wu 个石子。
因为你准备了ansu个石子,u点需要wu个石子放上,那么放完之后,他的子树上的石子就可以取回来了,也就是ansu-wu个,这些也就是节点u的孩子所需石子数和。
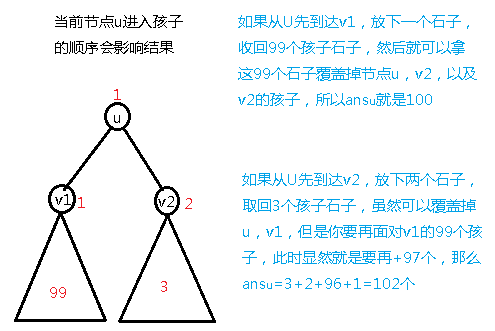
于是考虑影响问题答案的显然是从 u 进入每个孩子的顺序,由于最多有两个孩 子,直接比较一下就可以知道先进入哪个孩子更优秀了。时间复杂度 O(n)
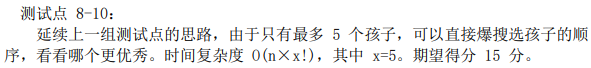
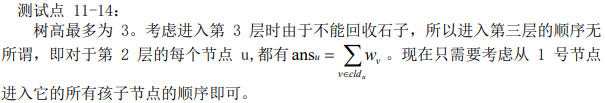


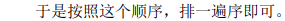

代码
#include <cstdio> #include <vector> #include <algorithm> const int maxn = 100010; int n; int MU[maxn], ans[maxn]; //MU也就是W std::vector<int>son[maxn]; void dfs(const int u); bool cmp(const int &_a, const int &_b); int main() { freopen("yin.in", "r", stdin); freopen("yin.out", "w", stdout); scanf("%d", &n); for (int i = 2, x; i <= n; ++i) { scanf("%d", &x); son[x].push_back(i); } for (int i = 1; i <= n; ++i) { scanf("%d", MU + i); //数组名+一个东西 这是指针的写法 //相当于scanf("%d",&MU[i]); } dfs(1); for (int i = 1; i < n; ++i) { printf("%d ", ans[i]); } printf("%d ", ans[n]); return 0; } void dfs(const int u) { for (auto v : son[u]) { //遍历u的所有子节点 dfs(v); } std::sort(son[u].begin(), son[u].end(), cmp); //按照差值不升序排序 int _ret = 0; //此时U节点的所有子节点已经算出来了,准备计算U节点 for (auto v : son[u]) { //叶节点没有儿子就不会for循环 if (_ret >= ans[v]) //上一个子节点收回的石子足够摆当前节点,就摆上 { _ret -= ans[v]; //ret摆完之后更新 } else { ans[u] += ans[v] - _ret; //收回的石子不够放了,往上补 _ret = ans[v] - MU[v]; //遍历完U的儿子V节点对应的子树后,收回除了 U的儿子v以外所有节点上的石头 } } ans[u] += std::max(0, MU[u] - _ret); //深搜,会先到达所有叶节点,并且所有叶节点的ans=w[i] } inline bool cmp(const int &_a, const int &_b) { return (ans[_a] - MU[_a]) > (ans[_b] - MU[_b]); }





题解
1.可以通过前4个任务点的代码QWQ
因为我们看到每封信最多只会有30个字符对吧,那么每次询问给出一个询问区间的时候,我们就可以比对每一位的字符
比如我们比对到了第 i 位,询问区间从头到尾枚举看一看,对于这一位,有几个0,几个1,几个?
如果既有0又有1,那么显然是无解的
如果只有0和?,那么这一位只可以为0,也就是?只能被填成0
如果只有1和?,同上
如果全是?,那么既可以填0,又可以填1,也就是有2种方案
我们把所有位都枚举了一遍,那么可能会出现结果:无解,有唯一解,有解但不唯一;对于最后一种情况显然是?的数目影响的,乘法分布原理 2cnt , cnt表示?的数目
代码
45‘代码 后边超时辣
#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<algorithm> #include<cmath> using namespace std; string s[100009],s1; int n,m,q; int qus,num,l,r; long long ans=0; int main() { freopen("lin.in","r",stdin); freopen("lin.out","w",stdout); scanf("%d%d%d",&n,&m,&q); if(q==0) return 0; for(int i=1;i<=m;i++) cin>>s[i]; for(int i=1;i<=q;i++) { ans=0; scanf("%d",&qus); if(qus==0) { scanf("%d%d",&l,&r); int flag=520,cnt=0; for(int j=0;j<n;j++) { if(flag==0) break; bool glf=0; char mp; mp=s[l][j]; if(mp!='?') glf=0; else glf=1; for(int k=l+1;k<=r;k++) { if(s[k][j]!='?') { if(mp=='?') { glf=1; mp=s[k][j]; continue; } if(mp!='?'&&mp!=s[k][j]) { flag=0; continue; } } else if(s[k][j]=='?') { if(glf==0) glf=1; } } if(mp!='?') glf=0; cnt+=glf; } if(flag==0) {printf("0 ");} else { ans=pow(2,cnt); printf("%ld ",ans); } } if(qus==1) { scanf("%d",&num); cin>>s1; s[num]=s1; } } return 0; }
我百分之200的错误都是因为脑残,下面这个是整理了一下(貌似并不可以多得分)
#include<bits/stdc++.h> using namespace std; int n,m,q; string s[100010],s1; int opt,l,r,pos; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int main() { freopen("lin.in","r",stdin); freopen("lin.out","w",stdout); n=read(); m=read(); q=read(); for(int i=1;i<=m;i++) cin>>s[i]; for(int i=1;i<=q;i++) { opt=read(); if(opt==1) { pos=read(); cin>>s1; s[pos]=s1; } else { l=read();r=read(); long long ans; int flag=1,cnt=0; for(int j=0;j<n;j++) { if(flag==0) break; int flag0=0,flag1=0,flag2=0; for(int k=l;k<=r;k++) { if(s[k][j]=='0') flag0++; if(s[k][j]=='1') flag1++; if(s[k][j]=='?') flag2++; } if(flag0!=0&&flag1!=0) { flag=0; continue; } else if(flag2==(r-l+1)) cnt++; } if(flag==0) ans=0; else ans=pow(2,cnt); printf("%ld ",ans); } } return 0; }
当然也可以用按位与维护

2.考虑正解:线段树

代码
忍不了这个指针了
#include <cstdio> template <typename T> inline void qr(T &x) { char ch = getchar(), lst = ' '; while ((ch > '9') || (ch < '0')) lst = ch, ch=getchar(); while ((ch >= '0') && (ch <= '9')) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar(); if (lst == '-') x = -x; } //快读 const int maxn = 100010; int n, m, q; char s[maxn][35]; //每封信的内容 #ifdef ONLINE_JUDGE int Ans; #endif struct Tree { Tree *ls, *rs; int l, r, x, y; bool leg; //是否合法 Tree() { ls = rs = NULL; l = r = x = y = 0; leg = true; //先假定合法 } void pushup() { //构造a1,a2,b1,b2 if (!(this->ls->leg && this->rs->leg)) { this->leg = false; } else { if ((this->ls->x & this->rs->x) & (this->ls->y ^ this->rs->y)) { this->leg = false; } else { this->leg = true; this->x = this->ls->x | this->rs->x; this->y = this->ls->y | this->rs->y; } } } }; Tree *rot; //线段树的根 void ReadStr(char *p); //指针 快读 void Update(const int x); void Query(const int l, const int r); void update(Tree *const u, const int p); //修改 Tree query(Tree *u, const int l, const int r); //查询 void build(Tree *const u, const int l, const int r); //建树 int main() { freopen("lin.in", "r", stdin); freopen("lin.out", "w", stdout); qr(n); qr(m); qr(q); for (int i = 1; i <= m; ++i) { ReadStr(s[i] + 1); } build(rot = new Tree, 1, m); //建树 int opt, l, r; while (q--) { opt = 0; qr(opt); if (opt == 0) { //查询 l = r = 0; qr(l); qr(r); Query(l, r); } else { l = 0; qr(l); ReadStr(s[0] + 1); Update(l); //修改第一个 } } #ifdef ONLINE_JUDGE //鬼知道干啥的 printf("%d ", Ans); #endif return 0; } void ReadStr(char *p) { do *p = getchar(); while ((*p != '0') && (*p != '1') && (*p != '?')); do *(++p) = getchar(); while ((*p == '0') || (*p == '1') || (*p == '?')); *p = 0; } void build(Tree *const u, const int l, const int r) { if ((u->l = l) == (u->r = r)) { //当前区间在要建的区间内 for (int i = 1; i <= n; ++i) { if (s[l][i] != '?') { u->x |= 1 << i; if (s[l][i] == '1') { u->y |= 1 << i; } } } } else { //不在 int mid = (l + r) >> 1; build(u->ls = new Tree, l, mid); build(u->rs = new Tree, mid + 1, r); u->pushup(); } } Tree query(Tree *u, const int l, const int r) { if ((u->l > r) || (u->r < l)) return Tree(); //当前区间完全不在查询区间 if ((u->l >= l) && (u->r <= r)) return *u; //完全在 Tree _ret; auto ll = query(u->ls, l, r), rr = query(u->rs, l, r); //否则递归来求 _ret.ls = ≪ _ret.rs = &rr; _ret.pushup(); return _ret; } void Query(const int l, const int r) { auto _ret = query(rot, l, r); if (!_ret.leg) { //不合法输出‘0’ #ifndef ONLINE_JUDGE puts("0"); #endif } else { int ans = 1; for (int i = 1; i <= n; ++i) if (!(_ret.x & (1 << i))) { ans <<= 1; } #ifdef ONLINE_JUDGE Ans ^= ans; #else printf("%d ", ans); #endif } } void update(Tree *u, const int p) { //修改第p个 if (u->ls) { //寻找p if (u->ls->r >= p) { //左子树右端点比p大 update(u->ls, p); } else { update(u->rs, p); } u->pushup(); //把子节点的信息合并到父节点 } else { *u = Tree(); u->l = u->r = p; for (int i = 1; i <= n; ++i) { if (s[0][i] != '?') { u->x |= 1 << i; if (s[0][i] == '1') { u->y |= 1 << i; } } } } } void Update(const int x) { update(rot, x); //修改 }
拒绝理解Zay的代码
放一只water lift的代码(线段树板子)
#include <bits/stdc++.h> using namespace std; template <class T> inline void read(T &num) { bool flag = 0; num = 0; char c = getchar(); while ((c < '0' || c > '9') && c != '-') c = getchar(); if (c == '-') { flag = 1; c = getchar(); } num = c - '0'; c = getchar(); while (c >= '0' && c <= '9') num = (num << 3) + (num << 1) + c - '0', c = getchar(); if (flag) num *= -1; } template <class T> inline void output(T num) { if (num < 0) { putchar('-'); num = -num; } if (num >= 10) output(num / 10); putchar(num % 10 + '0'); } template <class T> inline void outln(T num) { output(num); putchar(' '); } template <class T> inline void outps(T num) { output(num); putchar(' '); } const int N = 31, M = 100010; int n, m, q; struct segment { char val[M]; bool all1[M * 4]; bool all0[M * 4]; void init(int node, int nl, int nr)//这是个正常的线段树的板子(虽然位置好像不大正常) { if (nl < nr) { int mid = (nl + nr) >> 1; init(node * 2, nl, mid); init(node * 2 + 1, mid + 1, nr); all1[node] = all1[node * 2] & all1[node * 2 + 1]; all0[node] = all0[node * 2] & all0[node * 2 + 1]; } else { if (val[nl] == '?') all1[node] = all0[node] = 1; else { all1[node] = val[nl] == '1'; all0[node] = val[nl] == '0'; } } } void modify(int node, int nl, int nr, int x, char va) { if (val[x] == va) return; if (nl < nr) { int mid = (nl + nr) >> 1; if (x <= mid) { modify(node * 2, nl, mid, x, va); } else { modify(node * 2 + 1, mid + 1, nr, x, va); } all1[node] = all1[node * 2] & all1[node * 2 + 1]; all0[node] = all0[node * 2] & all0[node * 2 + 1]; } else { if (va == '?') all1[node] = all0[node] = 1; else { all1[node] = va == '1'; all0[node] = va == '0'; } val[x] = va; } } pair<bool, bool> query(int node, int nl, int nr, int l, int r) { if (l <= nl && r >= nr) { return make_pair(all1[node], all0[node]); } int mid = (nl + nr) >> 1; bool a1 = true, a0 = true; if (l <= mid) { auto lo = query(node * 2, nl, mid, l, r); a1 &= lo.first; a0 &= lo.second; } if (r >= mid + 1) { auto lo = query(node * 2 + 1, mid + 1, nr, l, r); a1 &= lo.first; a0 &= lo.second; } return make_pair(a1, a0); } void dfs(int node, int nl, int nr) { if (nl < nr) { int mid = (nl + nr) >> 1; dfs(node * 2, nl, mid); dfs(node * 2 + 1, mid + 1, nr); } outps(nl); outps(nr); outps(all1[node]); outln(all0[node]); } } segs[N]; int main() { freopen("lin.in", "r", stdin); freopen("lin.out", "w", stdout); read(n); read(m); read(q); char ch; for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { do { ch = getchar(); } while (ch == ' ' || ch == ' ' || ch == ' ' || ch == ' ' || ch == '�'); segs[j].val[i] = ch; } } for (int i = 1; i <= n; i++) { segs[i].init(1, 1, m); } while (q--) { bool opt; read(opt); if (opt == 0) { int l, r; read(l); read(r); int ans = 1; for (int i = 1; i <= n; i++) { auto lo = segs[i].query(1, 1, m, l, r); ans *= (lo.first + lo.second); } outln(ans); } else { int pos; read(pos); for (int i = 1; i <= n; i++) { do { ch = getchar(); } while (ch == ' ' || ch == ' ' || ch == ' ' || ch == ' ' || ch == '�'); segs[i].modify(1, 1, m, pos, ch); } } } }
彩蛋:
考试暴露了很多小问题
1.文件的读写
安利一个方法:如何比较自己的代码ans和答案out是否一致(不仅是用在NOIP上,还有NOI,IOI)
(1)键盘按住 shift 键,同时鼠标右键单击
(2)会崩出一个会话框,点击“在此处打开命令窗口”,win10不大一样,好像是f**忘了
(3)就会出现这个东西
不输入cmd 也可以,因为它本身就是cmd
(4)输入 fc 文件1 文件2
如果不同的话
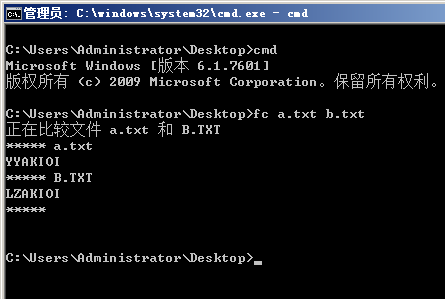
如果相同的话
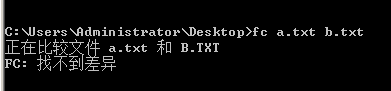
这样你就可以看看自己的答案对不对,错在哪里QWQ
2.数据分治
也就是对于不同的子任务你可以用不同的方法解决掉,从而骗取更多分数
3.编译&加文件的顺序
大型考试的时候呢,如果你代码一旦进行了修改,那么一定要重新试一遍样例
freopen就不要注释掉啦
4.题目难度和顺序安排不一定有瓜