最长上升子序列 (反正这个oj我做不了)
洛谷:AT2827 LIS
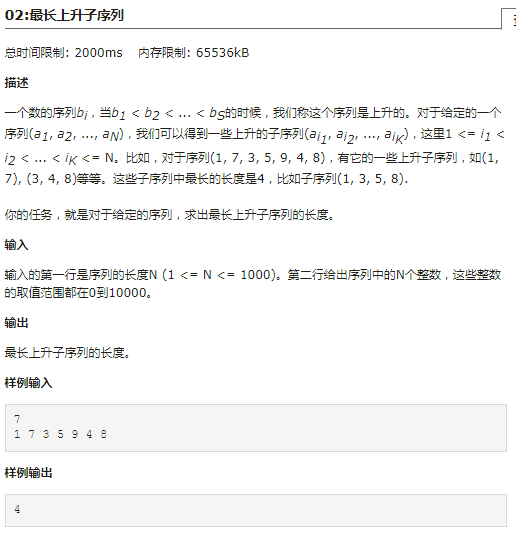
题解:
1.DP(TLE)
这是一道最为经典的完全用动态规划来解决的问题。
◦ 设dp[i]为以a[i]为末尾的最长上升子序列的长度。
◦ 最后的答案就是我枚举一下最长上升子序列的结束位置,然后取一个dp[i]最大值即可。
◦ 问题是如何求这个数组?
◦ 那我们回过头来想一想最开始说的动态规划的基本思想,从小的问题推出大的问题。
◦ 假设我们知道了dp[1..(i-1)],我们怎么才能根据这些信息推出来dp[i]。
◦ 再次强化一下定义:dp[i]表示以i结尾的最长上升子序列长度。
◦ 我们只需要枚举这个上升子序列倒数第二个数是什么就好了。
◦ 状态转移:dp[i]=max{ dp[j] | a[j]<a[i] && j<i } +1 ; (dp记录的是长度)
◦ 之前的例子:
◦ A:{2 , 5 , 3 , 4 , 1 , 7 , 6}
◦ dp[1]=1;
◦ dp[2]=max{dp[1]}+1;
◦ dp[3]=max{dp[1]}+1;
◦ dp[4]=max{dp[1],dp[3]}+1;
◦ 时间复杂度 O(n^2)。
◦ 在这个问题的分析中,突破口?
◦ 1:设计出了dp[1..n]这个可以储存以i结尾的子序列中最优的答案,这个状态表示。
◦ 2:通过分析问题成功能将当前状态的最优值能过由之前状态转移出来。dp[i]=max{ dp[j] | a[j]<a[i] && j<i } +1 ,状态转移。
>最长上升子序列核心代码
◦ 设dp[i]为以a[i]为末尾的最长上升子序列的长度。
◦ 状态转移:dp[i]=max{ dp[j] | a[j]<a[i] && j<i } +1 ;

>下面是DP玩火TLE代码
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<string> #include<cstring> #include<queue> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } const int maxn=1e5+10; int n,ans=0; int a[maxn],dp[maxn]; int main() { n=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int i=1;i<=n;i++) { dp[i]=1; for(int j=1;j<i;j++) if(a[j]<a[i]&&dp[j]+1>dp[i]) dp[i]=dp[j]+1; ans=max(ans,dp[i]); } printf("%d",ans); return 0; }
2.lower_bound优化
我们可以设最长上升子序列的长度为len
d[len]表示长度为len的最长上升子序列里最后一个数
当然,边界条件为
len=1
d[len]=a[1];
从第二个枚举所给序列的所有元素
设当前为i
当a[i]比d[len]大的时候,就加入到d数组,更新len和队尾
否则,如果a[i]!=d[len]
那就找到队列中第一个大于等于a[i]的数,用a[i]替代它,因为a[i]比原来的更有潜力形成一个新的最长上升子序列
此处采用lower_bound优化,相当于一个二分查询,一次查询O(logn)
但是如果用两层DP的话大多数是会直接TLE O(n^2)
>下面是lower_bound优化AC代码:
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<string> #include<cstring> #include<queue> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } const int maxn=1e5+10; int n,len=0; int a[maxn],d[maxn]; int main() { n=read(); for(int i=1;i<=n;i++) a[i]=read(); d[++len]=a[1]; for(int i=2;i<=n;i++) { if(a[i]>d[len]) d[++len]=a[i]; else d[lower_bound(d+1,d+len+1,a[i])-d]=a[i]; //返回一个迭代器 } printf("%d",len); return 0; }
