欧拉函数
在数论,对正整数n,欧拉函数是小于n的正整数中与n互质的数的数目(φ(1)=1)。
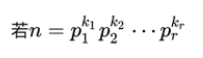
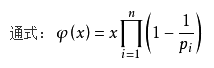
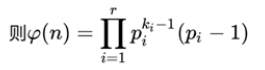
其中p1, p2……pn为x的所有质因数,x是不为0的整数
分解n=p1q1 * p2q2 * p3q3 * ……* pkqk
φ(n)= n*(1 - 1/p1) *(1 - 1/p2) *(1 - 1/p3)*……. *(1 - 1/pk)
= p1q1 * (1 - 1/p1) * p2q2 * (1 - 1/p2) * p3q3 * (1 - 1/p3) *…..* pkqk * (1 - 1/pk)
= p1q1 * ( (p1 – 1)/p1 ) * p2q2 * ( (p2 – 1)/p2 ) * p3q3 * ( (p3- 1)/p3 ) *…..* pkqk * ( (pk – 1)/pk )
= p1q1-1 * (p1 – 1) * p2q2-1 * (p2 – 1) * p3q3-1 * (p3- 1) *…..* pkqk-1 * (pk – 1)
那么对于一个素数,显然 φ(p)= p-1
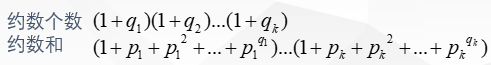

代码实现利用到了线性筛唉
g[n]表示n的因子个数
求一个数约数的个数,假设把它分解完了,那么g[i]=(1+q1)(1+q2)….(1+qn)
其实就是乘法原理啊,对于每个因子都可以选指数为0次,1次…q1次,一共(q1+1)种情况
phi[ ]是欧拉函数,欧拉函数是积性函数
证明: 假设n,m互质,那么他们一定没有相同的质因子
那么n=p1q1 * p2q2 * p3q3 * ……* pkqk
m=t1l1 * t2l2 * t3l3 * ……* tklk
假设k=n*m
那么显然φ(k)=φ(n)*φ(m)
/*欧拉筛 筛数 i 选取一个素数 p 把 p * i 筛掉 此时会检查 i 的最小素因子是否是p 所以有两种可能: 1、i 和 p 互素 phi[i * p] = phi[i] * phi[p] 2、i 的最小素因子刚好是 p phi[i * p] = phi[i] * p */ bool notprime[] int tot, prime[], e[]; int phi[];// phi 是欧拉函数 int g[]; // g[n]表示n的因子个数 int f[]; // f[n]表示n的最小素因子的次数 // f[12] = 2; // f[81] = 4; void sieve(int n) { for (int i = 2; i <= n; i++) { if (!notprime[i]) { prime[tot++] = i; e[i] = i; phi[i] = i - 1; g[i] = 2; f[i] = 1; } for (int j = 0; j < tot && (k = prime[j] * i) < n; j++) { e[k] = prime[j]; notprime[k] = true; if (e[i] == prime[j]) { phi[k] = phi[i] * prime[j]; //i和prime[j]不互质 f[k] = f[i] + 1; g[k] = g[i] / (f[i] + 1) * (f[k] + 1); break; } else { phi[k] = phi[i] * phi[prime[j]]; //i和prime[j]互质 g[k] = g[i] * g[prime[j]]; f[k] = 1; } } } }
欧拉定理
![]()
![]()