红黑树简介:
所谓红黑树,就是平衡的扩充二叉搜索树,红黑树与AVL都是BST的平衡版本,相比AVL的完全平衡,红黑树只要求局部平衡,因此当向红黑树中插入和删除节点时,需要的调整比AVL要少,统计性能要好于AVL树,C++ STL中的map、set、multimap和multiset都应用了红黑树的变体。
红黑树是特殊的二叉查找树,意味着它满足二叉查找树的特征:任意一个节点所包含的键值,大于等于左孩子的键值,小于等于右孩子的键值
当数据以升序或降序插入时,二叉搜索树的性能就会下降到最低,但是红-黑树的自我修复功能保证了即使在最坏的情况下,也能保证时间复杂度在O(logN)的级别上。
红黑树是满足下面红黑性质的二叉搜索树:
1. 每个节点,不是红色就是黑色的;
2. 根节点是黑色的;
3. 如果一个节点是红色的,则它的两个子节点是黑色的;
4. 对每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点;
5. 每个叶子节点都是黑色的(这里的叶子节点是指的空节点)
红黑树的特点:
1.每个节点不是红色就是黑色的;
2.根节点总是黑色的;
3.如果节点是红色的,则它的子节点必须是黑色的(反之不一定);
4.从根节点到叶节点或空子节点的每条路径,必须包含相同数目的黑色节点(即相同的黑色高度)。
在红-黑树中插入的节点都是红色的,这不是偶然的,因为插入一个红色节点比插入一个黑色节点违背红-黑规则的可能性更小。原因是:插入黑色节点总会改变黑色高度(违背规则4),但是插入红色节点只有一半的机会会违背规则3。另外违背规则3比违背规则4要更容易修正。
红黑树的修正:改变节点颜色、左旋和右旋。
变色:

左旋:
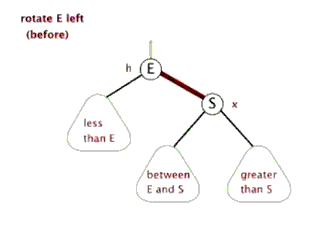
右旋:
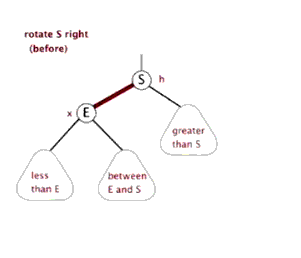
参考文章:
https://blog.csdn.net/eson_15/article/details/51144079