1.双端队列介绍
在介绍双端队列之前,我们需要先介绍队列的概念。和栈相对应,在许多算法设计中,需要一种"先进先出(First Input First Output)"的数据结构,因而一种被称为"队列(Queue)"的数据结构被抽象了出来(因为现实中的队列,就是先进先出的)。
队列是一种线性表,将线性表的一端作为队列的头部,而另一端作为队列的尾部。队列元素从尾部入队,从头部出队(尾进头出,先进先出)。
双端队列(Double end Queue)是一种特殊的队列结构,和普通队列不同的是,双端队列的线性表两端都可以进行出队和入队操作。当只允许使用一端进行出队、入队操作时,双端队列等价于一个栈;当限制一端只能出队,另一端只能入队时,双端队列等价于一个普通队列。
简洁起见,下述内容的"队列"默认代表的就是"双端队列"。
2.双端队列ADT接口
/** * 双端队列 ADT接口 * */ public interface Deque<E>{ /** * 头部元素插入 * */ void addHead(E e); /** * 尾部元素插入 * */ void addTail(E e); /** * 头部元素删除 * */ E removeHead(); /** * 尾部元素删除 * */ E removeTail(); /** * 窥视头部元素(不删除) * */ E peekHead(); /** * 窥视尾部元素(不删除) * */ E peekTail(); /** * @return 返回当前队列中元素的个数 */ int size(); /** * 判断当前队列是否为空 * @return 如果当前队列中元素个数为0,返回true;否则,返回false */ boolean isEmpty(); /** * 清除队列中所有元素 * */ void clear(); /** * 获得迭代器 * */ Iterator<E> iterator(); }
3.双端队列实现细节
3.1 双端队列基于数组的实现(ArrayDeque)
双端队列作为一个线性表,一开始也许会考虑能否像栈一样,使用向量作为双端队列的底层实现。
但是仔细思考就会发现:在向量中,头部元素的插入、删除会导致内部元素的整体批量的移动,效率很差。而队列具有"先进先出"的特性,对于频繁入队,出队的队列容器来说,O(n)时间复杂度的单位操作效率是无法容忍的。因此我们必须更进一步,从更为基础的数组结构出发,实现我们的双端队列。
3.1.1 数组双端队列实现思路:
在进行代码细节的展开之前,让我们先来理解以下基本思路:
1.和向量一样,双端队列在内部数组容量不足时,能和向量一样动态的扩容。
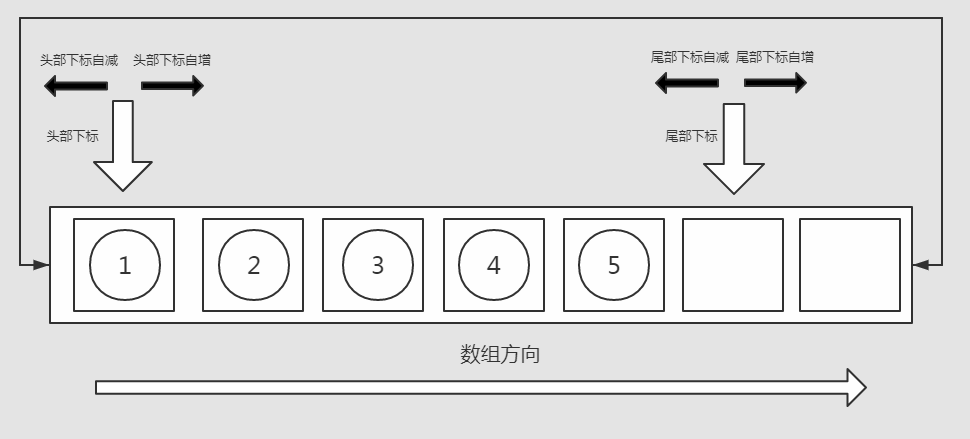
2.双端队列内部维护着"头部下标"、"尾部下标"。头部下标指向的是队列中第一位元素,尾部下标指向的是下一个尾部元素插入的位置。
从头部下标起始,到尾部下标截止(左闭右开区间),连续保存着队列中的全部元素。在元素出队,入队时,通过移动头尾下标,进行队列中元素的插入、删除,从而避免了类似向量中大量内部元素的整体移动。
当头部元素入队时,头部下标向左移动一位;头部元素出队时,头部下标向右移动一位。
当尾部元素入队时,尾部下标向右移动一位;尾部元素出队时,尾部下标向左移动一位。
3.当元素下标的移动达到了边界时,需要将数组从逻辑上看成一个环,其头尾是相邻的:
下标从数组第0位时,向左移动一位,会跳转到数组的最后一位。
下标从数组最后一位时,向右移动一位,会跳转到数组的第0位。
下标越界时的跳转操作,在细节上是通过下标取模实现的。
3.1.2 队列的基本属性:
只有当队列为空时,头部节点和尾部节点的下标才会相等。
/** * 基于数组的 双端队列 * */ public class ArrayDeque<E> implements Deque<E>{ /** * 内部封装的数组 * */ private Object[] elements; /** * 队列默认的容量大小 * */ private static final int DEFAULT_CAPACITY = 16; /** * 扩容翻倍的基数 * */ private static final int EXPAND_BASE = 2; /** * 队列头部下标 * */ private int head; /** * 队列尾部下标 * */ private int tail; /** * 默认构造方法 * */ public ArrayDeque() { //:::设置数组大小为默认 this.elements = new Object[DEFAULT_CAPACITY]; //:::初始化队列 头部,尾部下标 this.head = 0; this.tail = 0; } }
3.1.3 取模计算:
在jdk基于数组的双端队列实现中,强制保持内部数组容量为2的平方(初始化时容量为2的平方,每次自动扩容容量 * 2),因此其取模运算可以通过按位与(&)运算来加快计算速度。
取模运算在双端队列的基本接口实现中无处不在,相比jdk的双端队列实现,我们实现的双端队列实现更加原始,效率也较差。但相对的,我们的双端队列实现也较为简洁和易于理解。在理解了基础的实现思路之后,可以在这个初始版本的基础上进一步优化。
/** * 取模运算 * */ private int getMod(int logicIndex){ int innerArrayLength = this.elements.length; //:::由于队列下标逻辑上是循环的 //:::当逻辑下标小于零时 if(logicIndex < 0){ //:::加上当前数组长度 logicIndex += innerArrayLength; } //:::当逻辑下标大于数组长度时 if(logicIndex >= innerArrayLength){ //:::减去当前数组长度 logicIndex -= innerArrayLength; } //:::获得真实下标 return logicIndex; }
取模运算时间复杂度:
取模运算中只是进行了简单的整数运算,时间复杂度为O(1),而在jdk的双端队列实现中,使用位运算的取模效率还要更高。
3.1.4 基于数组的双端队列常用操作接口实现:
结合代码,我们再来回顾一下前面提到的基本思路:
1. 头部下标指向的是队列中第一位元素,尾部下标指向的是下一个尾部元素插入的位置。
2. 头部插入元素时,head下标左移一位;头部删除元素时,head下标右移一位。
尾部插入元素时,tail下标右移一位;尾部删除元素时,tail下标左移一位。
3. 内部数组被看成是一个环,下标移动到边界临界点时,通过取模运算来计算逻辑下标对应的真实下标。
@Override public void addHead(E e) { //:::头部插入元素 head下标左移一位 this.head = getMod(this.head - 1); //:::存放新插入的元素 this.elements[this.head] = e; //:::判断当前队列大小 是否到达临界点 if(head == tail){ //:::内部数组扩容 expand(); } } @Override public void addTail(E e) { //:::存放新插入的元素 this.elements[this.tail] = e; //:::尾部插入元素 tail下标右移一位 this.tail = getMod(this.tail + 1); //:::判断当前队列大小 是否到达临界点 if(head == tail){ //:::内部数组扩容 expand(); } } @Override @SuppressWarnings("unchecked") public E removeHead() { //:::暂存需要被删除的数据 E dataNeedRemove = (E)this.elements[this.head]; //:::将当前头部元素引用释放 this.elements[this.head] = null; //:::头部下标 右移一位 this.head = getMod(this.head + 1); return dataNeedRemove; } @Override @SuppressWarnings("unchecked") public E removeTail() { //:::获得尾部元素下标(左移一位) int lastIndex = getMod(this.tail - 1); //:::暂存需要被删除的数据 E dataNeedRemove = (E)this.elements[lastIndex]; //:::设置尾部下标 this.tail = lastIndex; return dataNeedRemove; } @Override @SuppressWarnings("unchecked") public E peekHead() { return (E)this.elements[this.head]; } @Override @SuppressWarnings("unchecked") public E peekTail() { //:::获得尾部元素下标(左移一位) int lastIndex = getMod(this.tail - 1); return (E)this.elements[lastIndex]; }
队列常用接口时间复杂度:
基于数组的队列在访问头尾元素时,进行了一次取模运算获得真实下标,由于数组的随机访问是常数时间复杂度(O(1)),因此队列常用接口的时间复杂度都为O(1),效率很高。
3.1.5 扩容操作:
可以看到,在入队插入操作结束后,会判断当前队列容量是否已经到达了临界点。
前面提到,只有在队列为空时,头部下标才会和尾部下标重合;而当插入新的入队元素之后,使得头部下标等于尾部下标时,说明内部数组的容量已经达到了极限,需要进行扩容才能容纳更多的元素。
我们举一个简单的例子来理解扩容操作:
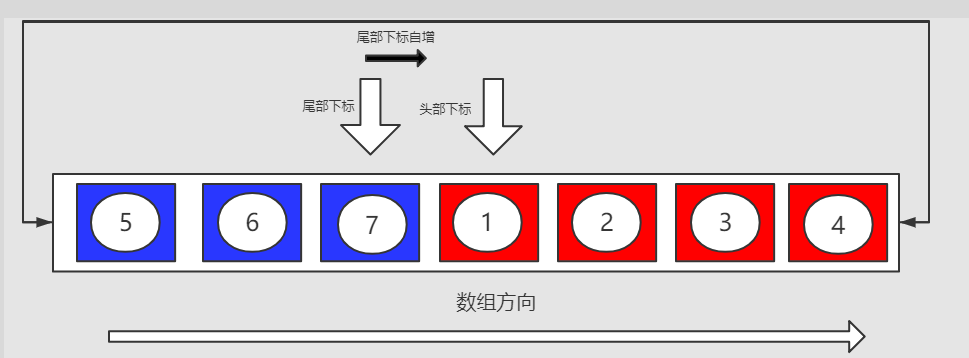
尾部下标为2.头部下标为3,队列内的元素为头部下标到尾部下标(左闭右开)中的元素排布为(1,2,3,4,5,6)。
目前队列刚刚在下标为2处的尾部入队元素"7"。尾部下标从2向右移动一位和头部下标重合,此时队列中元素排布为(1,2,3,4,5,6,7),此时需要进行一次扩容操作。
在扩容完成之后,我们希望让队列的元素在内部数组中排列的更加自然:
1. 队列中元素的顺序不变,依然是(1,2,3,4,5,6,7),内部数组扩容一定的倍数(两倍)
2. 队列中第一个元素将位于内部数组的第0位,队列中的元素按照头尾顺序依次排列下去
扩容的大概思路:
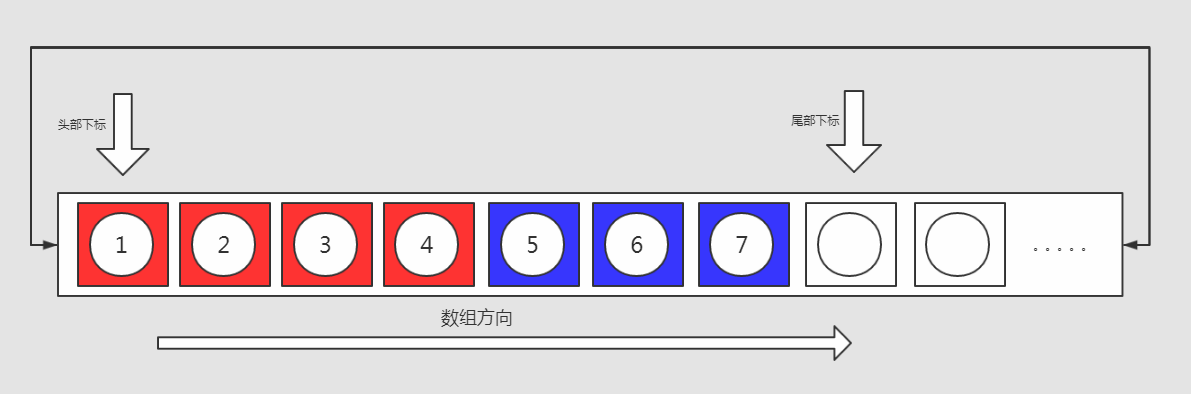
1. 将"头部下标"直至"当前内部数组尾部"的元素按照顺序整体复制到新扩容数组的起始位置(红色背景的元素)
2. 将"当前内部数组头部"直至"尾部下标"的元素按照顺序整体复制到新扩容数组中(位于第一步操作复制的数据区间之后)(蓝色背景的元素)
扩容前:
扩容后:
扩容代码的实现:
/** * 内部数组扩容 * */ private void expand(){ //:::内部数组 扩容两倍 int elementsLength = this.elements.length; Object[] newElements = new Object[elementsLength * EXPAND_BASE]; //:::将"head -> 数组尾部"的元素 复制在新数组的前面 (tips:使用System.arraycopy效率更高) for(int i=this.head, j=0; i<elementsLength; i++,j++){ newElements[j] = this.elements[i]; } //:::将"0 -> head"的元素 复制在新数组的后面 (tips:使用System.arraycopy效率更高) for(int i=0, j=elementsLength-this.head; i<this.head; i++,j++){ newElements[j] = this.elements[i]; } //:::初始化head,tail下标 this.head = 0; this.tail = this.elements.length; //:::内部数组指向 新扩容的数组 this.elements = newElements; }
扩容操作时间复杂度:
动态扩容的操作由于需要进行内部数组的整体copy,其时间复杂度是O(n)。
但是站在全局的角度,动态扩容只会在入队操作导致空间不足时偶尔的被触发,整体来看,动态扩容的时间复杂度为O(1)。
3.1.6 其它接口实现:
@Override public int size() { return getMod(tail - head); } @Override public boolean isEmpty() { //:::当且仅当 头尾下标相等时 队列为空 return (head == tail); } @Override public void clear() { int head = this.head; int tail = this.tail; while(head != tail){ this.elements[head] = null; head = getMod(head + 1); } this.head = 0; this.tail = 0; } @Override public Iterator<E> iterator() { return new Itr(); }
3.1.7 基于数组的双端队列——迭代器实现:
迭代器从头部元素开始迭代,直至尾部元素终止。
值得一提的是,虽然队列的api接口中没有提供直接删除队列中间(非头部、尾部)的元素,但是迭代器的remove接口却依然允许这种操作。由于必须要时刻保持队列内元素排布的连续性,因此在删除队列中间的元素后,需要整体的移动其他元素。
此时,有两种选择:
方案一:将"头部下标"到"被删除元素下标"之间的元素整体向右平移一位
方案二:将"被删除元素下标"到"尾部下标"之间的元素整体向左平移一位
我们可以根据被删除元素所处的位置,计算出两种方案各自需要平移元素的数量,选择平移元素数量较少的方案,进行一定程度的优化。
队列迭代器的remove操作中存在一些细节值得注意,我们使用一个简单的例子来帮助理解:
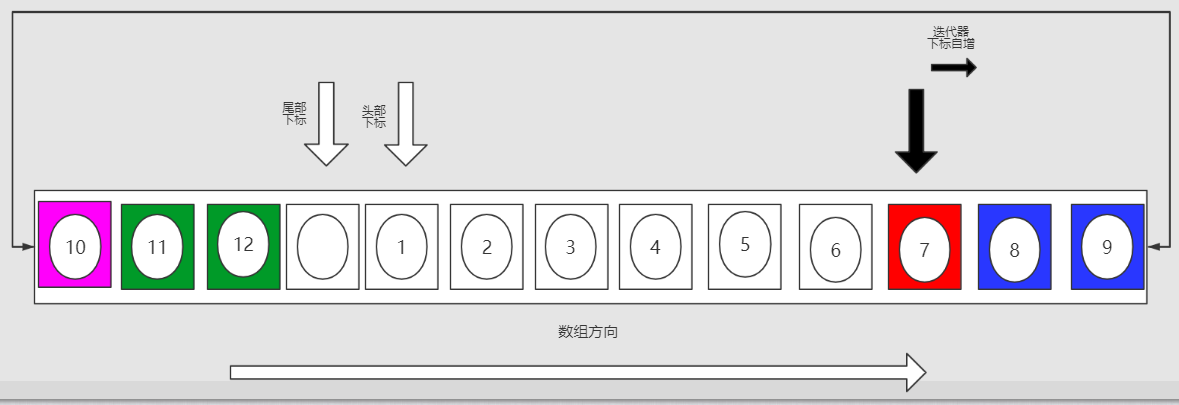
1. 当前队列在迭代时需要删除元素"7"(红色元素),采用方案一需要整体平移(1,2,3,4,5,6)六个元素,而方案二只需要整体平移(8,9,10,11,12)五个元素。因此采用平移元素更少的方案二,
2. 这时由于(8,9,10,11,12)五个元素被物理上截断了,所以主要分三个步骤进行平移。
第一步: 先将靠近尾部的 (8,9)两个元素整体向左平移一位(蓝色元素)
第二步: 将内部数组头部的元素(10),复制到内部数组的尾部(粉色元素)
第三部 : 将剩下的元素(11,12),整体向左平移一位(绿色元素)
remove操作执行前:
remove操作执行后:

迭代器代码实现:
在remove操作中有多种可能的情况,由于思路相通,可以通过上面的举例说明帮助理解。
/** * 双端队列 迭代器实现 * */ private class Itr implements Iterator<E> { /** * 当前迭代下标 = head * 代表遍历从头部开始 * */ private int currentIndex = ArrayDeque.this.head; /** * 目标终点下标 = tail * 代表遍历至尾部结束 * */ private int targetIndex = ArrayDeque.this.tail; /** * 上一次返回的位置下标 * */ private int lastReturned; @Override public boolean hasNext() { //:::当前迭代下标未到达终点,还存在下一个元素 return this.currentIndex != this.targetIndex; } @Override @SuppressWarnings("unchecked") public E next() { //:::先暂存需要返回的元素 E value = (E)ArrayDeque.this.elements[this.currentIndex]; //:::最近一次返回元素下标 = 当前迭代下标 this.lastReturned = this.currentIndex; //:::当前迭代下标 向后移动一位(需要取模) this.currentIndex = getMod(this.currentIndex + 1); return value; } @Override public void remove() { if(this.lastReturned == -1){ throw new IteratorStateErrorException("迭代器状态异常: 可能在一次迭代中进行了多次remove操作"); } //:::删除当前迭代下标的元素 boolean deleteFromTail = delete(this.currentIndex); //:::如果从尾部进行收缩 if(deleteFromTail){ //:::当前迭代下标前移一位 this.currentIndex = getMod(this.currentIndex - 1); } //:::为了防止用户在一次迭代(next调用)中多次使用remove方法,将lastReturned设置为-1 this.lastReturned = -1; } /** * 删除队列内部数组特定下标处的元素 * @param currentIndex 指定的下标 * @return true 被删除的元素靠近尾部 * false 被删除的元素靠近头部 * */ private boolean delete(int currentIndex){ Object[] elements = ArrayDeque.this.elements; int head = ArrayDeque.this.head; int tail = ArrayDeque.this.tail; //:::当前下标 之前的元素个数 int beforeCount = getMod(currentIndex - head); //:::当前下标 之后的元素个数 int afterCount = getMod(tail - currentIndex); //:::判断哪一端的元素个数较少 if(beforeCount < afterCount){ //:::距离头部元素较少,整体移动前半段元素 //:::判断头部下标 是否小于 当前下标 if(head < currentIndex){ //:::小于,正常状态 仅需要复制一批数据 //:::将当前数组从"头部下标"开始,整体向右平移一位,移动的元素个数为"当前下标 之前的元素个数" System.arraycopy(elements,head,elements,head+1,beforeCount); }else{ //:::不小于,说明存在溢出环 需要复制两批数据 //:::将数组从"0下标处"的元素整体向右平移一位,移动的元素个数为"从0到当前下标之间的元素个数" System.arraycopy(elements,0,elements,1,currentIndex); //:::将数组最尾部的数据设置到头部,防止被覆盖 elements[0] = elements[(elements.length-1)]; //:::将数组尾部的数据整体向右平移一位 System.arraycopy(elements,head,elements,head+1,(elements.length-head-1)); } //:::释放被删除元素的引用 elements[currentIndex] = null; //:::头部下标 向右移动一位 ArrayDeque.this.head = getMod(ArrayDeque.this.head + 1); //:::没有删除尾部元素 返回false return false; }else{ //:::距离尾部元素较少,整体移动后半段元素 //:::判断尾部下标 是否小于 当前下标 if(currentIndex < tail){ //:::小于,正常状态 仅需要复制一批数据 //:::将当前数组从"当前"开始,整体向左平移一位,移动的元素个数为"当前下标 之后的元素个数" System.arraycopy(elements,currentIndex+1,elements,currentIndex,afterCount); }else{ //:::不小于,说明存在溢出环 需要复制两批数据 //:::将数组从"当前下标处"的元素整体向左平移一位,移动的元素个数为"从当前下标到数组末尾的元素个数-1 ps:因为要去除掉被删除的元素" System.arraycopy(elements,currentIndex+1,elements,currentIndex,(elements.length-currentIndex-1)); //:::将数组头部的元素设置到末尾 elements[elements.length-1] = elements[0]; //:::将数组头部的数据整体向左平移一位,移动的元素个数为"从0到尾部下标之间的元素个数" System.arraycopy(elements,1,elements,0,tail); } //:::尾部下标 向左移动一位 ArrayDeque.this.tail = getMod(ArrayDeque.this.tail - 1);
//:::删除了尾部元素 返回true return true; } } }
3.2 基于链表的链式双端队列
和向量不同,双向链表在头尾部进行插入、删除操作时,不需要额外的操作,效率极高。
因此,我们可以使用之前已经封装好的的双向链表作为基础,轻松的实现一个链式结构的双端队列。限于篇幅,就不继续展开了,有兴趣的读者可以尝试自己完成这个任务。
4.双端队列性能
空间效率:
基于数组的双端队列:数组空间结构非常紧凑,效率很高。
基于链表的双端队列:由于链式结构的节点存储了相关联的引用,空间效率比数组结构稍低。
时间效率:
对于双端队列常用的出队、入队操作,由于都是在头尾处进行操作,数组队列和链表队列的执行效率都非常高(时间复杂度(O(1)))。
需要注意的是,由于双端队列的迭代器remove接口允许删除队列中间部位的元素,而删除中间队列元素的效率很低(时间复杂度O(n)),所以在使用迭代器remove接口时需要谨慎。
5.双端队列总结
至此,我们实现了一个基础的、基于数组的双端队列。要想更近一步的学习双端队列,可以尝试着阅读jdk的java.util.ArrayDeque类并且按照自己的思路尝试着动手实现一个双端队列。我个人认为,如果事先没有一个明确的思路,直接去硬看源代码,很容易就陷入细节之中无法自拔,"不识庐山真面目,只缘生在此山中"。
希望这篇博客能够让读者更好的理解双端队列,更好的理解自己所使用的数据结构,写出更高效,易维护的程序。
博客的完整代码在我的 github上:https://github.com/1399852153/DataStructures ,存在许多不足之处,请多多指教。