行文思路:
- 最小二乘法原理介绍
- 利用 leastsq() 函数进行最小二乘法拟合
- 拟合注意事项
- 利用curve_fit 进行最小二乘法拟合
- 总结:
- 参考文献
- 实现代码
一,最小二乘法拟合
最小二乘法是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配。优化是找到最小值或等式的数值解的问题。而线性回归就是要求样本回归函数尽可能好地拟合目标函数值,也就是说,这条直线应该尽可能的处于样本数据的中心位置。因此,选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。
假设有一组实验数据(xi,yi ), 事先知道它们之间应该满足某函数关系yi=f(xi),通过这些已知信息,需要确定函数f的一些参数。例如,如果函数f是线性函数f(x)=kx+b, 那么参数 k和b就是需要确定的值。
如果用p表示函数中需要确定的参数,那么目标就是找到一组p,使得下面的函数S的值最小:
当误差最小的时候可以理解为此时的系数为最佳的拟合状态。
scipy.optimization 子模块提供了函数最小值(标量或多维)、曲线拟合和寻找等式的根的有用算法。在optimize模块中可以使用 leastsq() 对数据进行最小二乘拟合计算。leastsq() 函数传入误差计算函数和初始值,该初始值将作为误差计算函数的第一个参数传入。计算的结果是一个包含两个元素的元组,第一个元素是一个数组,表示拟合后的参数;第二个元素如果等于1、2、3、4中的其中一个整数,则拟合成功,否则将会返回 mesg。下面是官方的文档介绍,只截取了主要的参数部分。
代码实现:
1,导入模块:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq2,一元二次方程的参数拟合,首先创建拟合数据。
x = np.linspace(-10,10,100) # 创建时间序列
p_value = [-2,5,10] # 原始数据的参数
noise = np.random.randn(len(x)) # 创建随机噪声
y = Fun(p_value,x)+noise*2 # 加上噪声的序列3,通过函数定义拟合函数的形式。
这里可以拟合任意的函数形式,这要能把它的表达式给出。
def Fun(p,x): # 定义拟合函数形式
a1,a2,a3 = p
return a1*x**2+a2*x+a34,定义残差项。
一般最小二乘法是求拟合函数和目标函数差的平方,这里之所以没有平方是应为在拟合函数的内部进行,这里不显式的表示。
def error (p,x,y): # 拟合残差
return Fun(p,x)-y 5, 进行拟合。
其中参数p0 为最小二乘法拟合的初值,初值的选取对于拟合时间和计算量影响很大,有事并对结果产生一定的影响。args() 中是除了初始值之外error() 中的所有参数的集合输入。
para =leastsq(error, p0, args=(x,y)) # 进行拟合
y_fitted = Fun (para[0],x) # 画出拟合后的曲线返回参数为一个包含拟合后参数的元组,可以通过中括号[] 取值的方式得到。
6,完整的代码如下:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
def Fun(p,x): # 定义拟合函数形式
a1,a2,a3 = p
return a1*x**2+a2*x+a3
def error (p,x,y): # 拟合残差
return Fun(p,x)-y
def main():
x = np.linspace(-10,10,100) # 创建时间序列
p_value = [-2,5,10] # 原始数据的参数
noise = np.random.randn(len(x)) # 创建随机噪声
y = Fun(p_value,x)+noise*2 # 加上噪声的序列
p0 = [0.1,-0.01,100] # 拟合的初始参数设置
para =leastsq(error, p0, args=(x,y)) # 进行拟合
y_fitted = Fun (para[0],x) # 画出拟合后的曲线
plt.figure
plt.plot(x,y,'r', label = 'Original curve')
plt.plot(x,y_fitted,'-b', label ='Fitted curve')
plt.legend()
plt.show()
print (para[0])
if __name__=='__main__':
main()最终拟合的参数结果:
[-1.99437662 5.03789895 10.00150115]
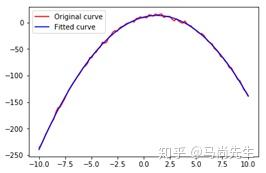
二, 使用curve_fit() 进行拟合
Note:使用 curve_fit(),主要的区别在于拟合函数的定义不同
def Fun(x, a1,a2,a3): # 定义拟合函数形式
return a1*x**2+a2*x+a3完整的代码:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
def Fun(x,a1,a2,a3): # 定义拟合函数形式
return a1*x**2+a2*x+a3
def error (p,x,y): # 拟合残差
return Fun(p,x)-y
def main():
x = np.linspace(-10,10,100) # 创建时间序列
a1,a2,a3 = [-2,5,10] # 原始数据的参数
noise = np.random.randn(len(x)) # 创建随机噪声
y = Fun(x,a1,a2,a3)+noise*2 # 加上噪声的序列
para,pcov=curve_fit(Fun,x,y)
y_fitted = Fun(x,para[0],para[1],para[2]) # 画出拟合后的曲线
plt.figure
plt.plot(x,y,'r', label = 'Original curve')
plt.plot(x,y_fitted,'-b', label ='Fitted curve')
plt.legend()
plt.show()
print (para)
if __name__=='__main__':
main()拟合结果
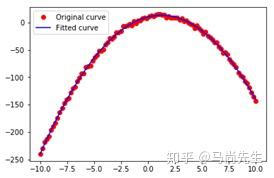
最终的拟合结果参数为:
[-2.00309373 5.00945061 10.30565526]
三, 多项式拟合
代码实现:
def main():
x = np.linspace(-10,10,100) # 创建时间序列
a1,a2,a3 = [-2,5,10] # 原始数据的参数
noise = np.random.randn(len(x)) # 创建随机噪声
y = Fun(x,a1,a2,a3)+noise*2 # 加上噪声的序列
plt.plot(x,y)
para=np.polyfit(x, y, deg = 2)
y_fitted = Fun(x,para[0],para[1],para[2])
plt.figure
plt.plot(x,y,'ro', label = 'Original curve')
plt.plot(x,y_fitted,'-b', label ='Fitted curve')
plt.legend()
plt.show()
print(para)
if __name__=='__main__':
main() 拟合结果为:
[-2.00532192 5.01626878 10.07612899]
总结:
本文主要讲了最小二乘法拟合曲线的实现方法,使用 leastsq() 和 curve_fit(),最后讲解了多项式的拟合poly.fit(). 最小二乘法的两个拟合大体的步骤是一样的,定义拟合范式,传入拟合参数,开始拟合得出拟合结果。对于简单的拟合函数两者的差别很小,但是复杂的,需要具体的分析。文章还会继续的分析拟合结果的含义,让我们对拟合的结果有更加透彻的理解,随心拟合。