前面说的直接插入排序,在某些情况下,它的效率是很高的,比如当要排序的序列很少的时候,或者排序的序列基本有序的时候。当然在现实中,要排序的序列基本上不可能满足这样的条件,如果碰到有非常多数的大序列需要排序,而且这些序列中的数也不是基本有序的,那我们该怎么办,这时候,如果还是使用直接插入排序,那么效率就非常低,很多人会想到,能不能把直接插入排序进行改进呢,你不是说对小序列效率比较高吗,那就把一个大的序列拆分成几个小序列,然后对它们分别进行排序。希尔排序就是这样一种改进的排序算法,它就是把一个大序列拆分成几个小的序列,然后对小的序列进行直接插入排序,最后合并在一起,那么这个大序列就变成基本有序了,这时候,再对整个基本有序的大序列进行一次直接插入排序,整个大序列就变成有序的了。
比如我们现在有一个序列{9,1,5,8,3,7,4,6,2},把它拆分成几个小的序列,可能有的人立即就想到拆分成{9,1,5},{8,3,7},{4,6,2},然后进行排序,排序后变成{1,5,9},{3,7,8},{2,4,6},合并在一起,进行直接插入排序,他们发现整个序列还是乱的,跟对原始数列直接进行插入排序没什么两样。这时因为,合并后的序列并没有满足“基本有序”这个条件。所谓基本有序,就是小的关键字在前面,大的关键字在后面,不大不小的在中间。上面的合并起来9跑到第三位去了,所以根本不能算基本有序。这时候,大家就会问了,那么怎样使整个序列是基本有序的呢。还是要把大序列进行拆分,只不过不是像上面的那样拆分,而是采用跳跃的形式进行拆分。也就是所相距某个增量的数字组成一个序列,再对这些序列进行排序,最后合并在一起,就变成基本有序了。
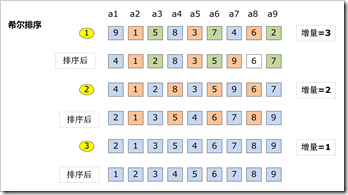
看下面的示意图(相同颜色的为一组):
第一次,我们取增量为3,那么整个序列分成了三组分别是{9,8,4},{1,3,6},{5,7,2},我们对这三个小序列分别进行插入排序,排序后合并得到的序列就是{4,1,2,8,3,5,9,6,7},它已经可以算基本有序,为了使它进一步基本有序,我们重新取一次分量,再来拆分一次;
第二次,我们取增量为2,那个整个序列被分成了两组,分别是{4,2,3,9,7},{1,8,5,6},我们再对这两个序列来进行直接插入排序,把排序好的合并到一起,最终的序列就是{2,1,3,5,4,6,7,8,9},这个时候,整个序列已经基本有序了。最后我们要取增量为1,再进行一次拆分。
第三次,我们取增量为1,有人会问取增量为1,不就没有没有拆分吗,是的,使用希尔排序,最后一次拆分时,增量一定要是1,也就是不管怎样拆分,最后一次一定是对整个序列进行一次直接插入排序。
有人会问,那为什么不一开始就用直接插入排序呢,我们在前面说过,直接插入排序在数据量少或者序列基本有序的情况下,效率比较高。如果一开始就进行直接插入排序,此时整个序列不是基本有效的,而且遇到数据量大时,效率也不高。而上面介绍的希尔排序,就是先进行拆分,对拆分后的小序列进行基本插入排序,在最后一次进行直接插入排序的时候,整个大的序列已经基本有序了。所以最后一次直接插入排序的效率应该是很高的。下面看具体的代码:
public List<int> SortByShell(List<int> sortList)
{
int incrementNum = sortList.Count / 3 + 1;//初始化的增量是数组长度除以3然后加上1
bool isEnd = false;
while (true)
{
for (int i = incrementNum; i <sortList.Count; i++)//在某个增量下,对拆分后的每个小序列进行排序
{
if (sortList[i] < sortList[i - incrementNum])//对每个小序列进行直接插入排序
{
int j;
int temp = sortList[i];
for ( j= i - incrementNum; j >=0&&temp< sortList[j]; j -= incrementNum)
{
sortList[j + incrementNum] = sortList[j];
}
sortList[j + incrementNum] = temp;
}
}
if (isEnd)
{
break;
}
incrementNum = incrementNum / 3 + 1;
if (incrementNum == 1)
{
isEnd = true;
}
}
return sortList;
}
通过上面,我们可以看出,希尔排序的关键是将相隔某个增量的数组成一个序列,进行直接插入排序,最以此来提高排序的效率。那么如何选取这个增量,是一个比较关键的问题,在上面的代码中,取的是数组长度除3然后再加上1。如何选取增量一直都没有什么好的办法,不过经过大量的研究,有一些取增量的经验,在网上可以找到相关的资料。不过不管增量如何取值,有一点是固定的,就是增量的最后一个值一定要是1,这样才能保证整个序列最后是有序的。经过证明,当取一个合理的增量时,希尔排序的时间复杂度为O(n 3/2),要好于直接排序的O(n 2)。