说到堆的相关知识,之前我在队列中也说过一些,而且优先队列就是使用的堆得思想,今天只是想主要说一下堆得上溢和下溢操作原理,也就是堆实现插入和删除的原理。
一、堆的基础知识
1、堆的定义
堆是一种类似于树的结构的数据结构,堆有孩子节点,所有子节点均小于大于或者小于根节点。
2、堆的分类
最大堆:子节点值均小于根节点的值,这样的堆叫做最大堆;
最小堆:子节点值均大于根节点的值,这样的堆叫做最小堆。
3、堆的图示
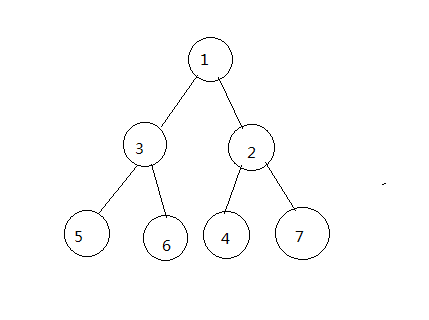
二、堆的上滤下滤(最小堆)
首先说一下堆的上溢和下溢的作用,堆的上溢操作主要是用来实现插入操作,堆的下溢操做主要是用来实现删除操作。
1、上滤
说道上滤操作,我觉得结合堆的插入操作比较好理解。插入操作可以分为以下几种方式:
(1)将新的节点插入最后的位置,记录当前位置为n
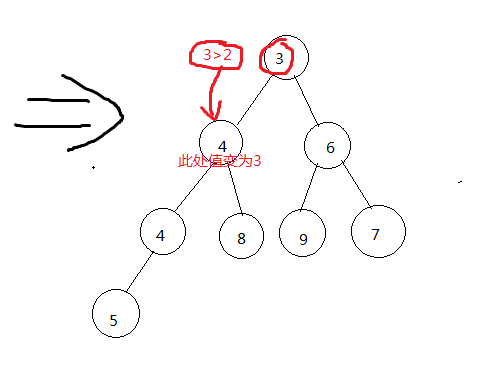
(2)取插入新节点的父节点(即位置为n/2)比较值与当前新节点的值的大小,若比插入的值小,则将父节点值赋值到位置为n节点处。若比插入的值大,则将要插入的节点值,赋值给n位置的节点上,然后结束上滤。
(3)取n/2位置的父节点,也就是(n/2)/2位置节点与插入的值比较大小,若比插入的值小,则将父节点值赋值到位置为n/2节点处。若比插入的值大,则将要插入的节点值,赋值给n/2位置的节点上,然后结束上滤。
(4)取(n/2)/2位置的父节点,也就是((n/2)/2)/2位置节点与插入的值比较大小,若比插入的值小,则将父节点值赋值到位置为(n/2)/2节点处。若比插入的值大,则将要插入的节点值,赋值给(n/2)/2位置的节点上,然后结束上滤。
.....一直重复上滤过程,也就父节点的值比插入的值小。
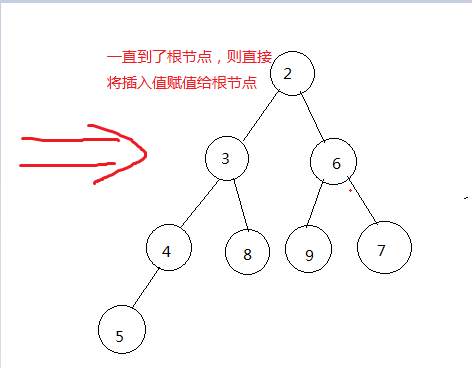
(5)直到最后根节点,将插入的节点值赋值给根节点,然后结束上滤。
例如:下图
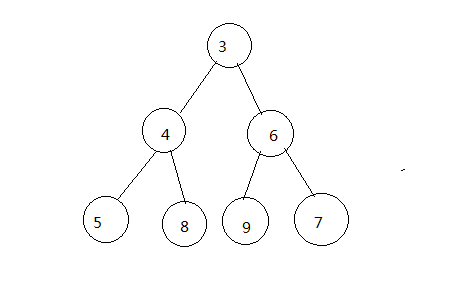
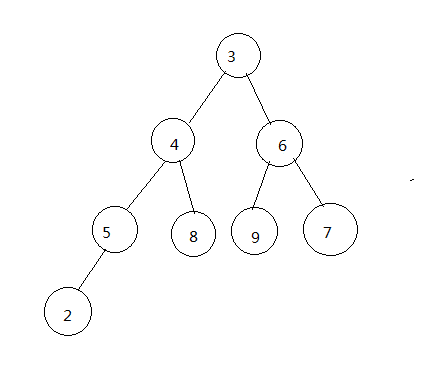
插入值为2的节点,操作入下:


2、下滤
说到下滤我觉得结合堆的删除操作一起来讲比较好理解。首先我们将删除的节点分类,无非两种一个是非叶子结点,也就是某一个子树的根,另一个为叶子结点。对于删除的是叶子结点直接删除,如果不是叶子结点则需要进行下滤操作。
删除操作分为以下几步:
(1)删除的节点是否是叶子元素,是叶子元素直接删除,删除的不是叶子节点,则需要进行下滤操作。
(2)下滤操作的具体:1)先找到要删除元素的位置,并记录该元素的位置n
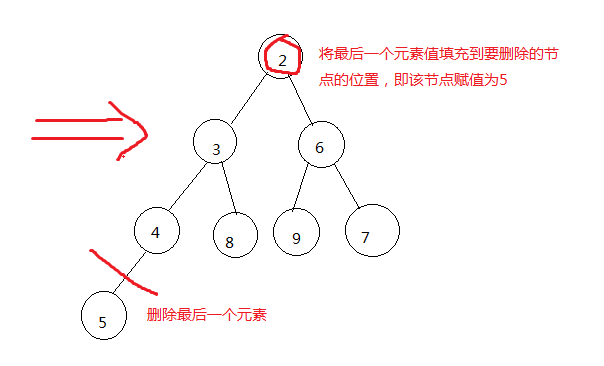
2)获取并删除该堆的最后一个元素,思想是前面的一个元素删除了,最后的元素必定会紧凑到前面的某一位置上,先将这个值暂且填充到删除的位置上,然 后调整位置
3)获取n位置的孩子节点中最小的值,记录该值的位置m,并且将该值与现在该位置的值比较大小,如果m位置的值比n位置值小的话,将m位置的值赋值 到n位置处,将n位置的值赋值 到m位置处;如果m位置的值比n位置值大的话,直接结束下溢过程。
4)获取m位置的孩子节点中最小的值,记录该值的位置k,并且将该值与现在该位置的值比较大小,如果k位置的值比m位置值小的话,将k位置的值赋值 到m位置处,将m位置的值赋值 到k位置处;如果k位置的值比m位置值大的话,直接结束下溢过程。
......一直重复上滤过程,也就孩子节点最小值比插入的值小,结束下溢过程。
5)直到最后叶节点,将插入的节点值赋值给叶节点,然后结束下滤。
例如:
删除值为2的节点


三、堆的删除(最小值删除)和插入操作代码(实质就是优先队列的相关操作)
以最小堆为例
代码示例:(Java)
1 public class PriorityQueue1 { 2 private final int DEFUALTSIZE=4;//默认的堆大小+1,即2的平方 3 private int []queue1;//默认底层的数组存储实现 4 private int nowQueueSize=0;//记录当前堆得元素的个数,队列的元素个数 5 //对优先队列进行相关的初始化,申请一些空间 6 public PriorityQueue1(){ 7 queue1=new int[DEFUALTSIZE]; 8 } 9 //给优先队列进行拓展空间存储大小 10 public void enlargeArray(int newSize){ 11 System.out.println("优先队列进行拓展一次空间"); 12 int []mark=queue1; 13 queue1=new int [newSize]; 14 for(int i=0;i<mark.length;i++){ 15 queue1[i]=mark[i]; 16 } 17 } 18 public void push(int m){ 19 //如果存储空间不够,申请新的空间 20 if(nowQueueSize==queue1.length-1){ 21 enlargeArray(queue1.length*2);//拓展的大小是拓展了堆(树)得下一层 22 } 23 //上溢操作 24 int markLocation=++nowQueueSize; 25 for(queue1[0]=m;queue1[markLocation/2]>m;markLocation/=2){ 26 queue1[markLocation]=queue1[markLocation/2]; 27 } 28 queue1[markLocation]=m; 29 //测试入队列后的数组元素分布 30 for(int i=1;i<=nowQueueSize;i++){ 31 System.out.print(queue1[i]+" "); 32 } 33 System.out.println(); 34 35 } 36 public int pop() throws Exception{ 37 if(nowQueueSize==0){ 38 throw new Exception("优先队列已空,不能进行出队列操作!"); 39 } 40 //优先队列的下溢操作 41 int mark=queue1[1]; 42 for(int i=1;i<nowQueueSize;){ 43 int markMin; 44 int markI; 45 if(2*i>nowQueueSize-1){ 46 queue1[i]=queue1[nowQueueSize]; 47 break; 48 }else if(2*i+1<=nowQueueSize-1){ 49 markMin=queue1[2*i]>queue1[2*i+1]?queue1[2*i+1]:queue1[2*i]; 50 markI=queue1[2*i]>queue1[2*i+1]?(2*i+1):(2*i); 51 if(queue1[nowQueueSize]<markMin){ 52 queue1[i]=queue1[nowQueueSize]; 53 break; 54 }else{ 55 queue1[i]=markMin; 56 i=markI; 57 } 58 }else{ 59 markMin=queue1[2*i]; 60 markI=2*i; 61 if(queue1[nowQueueSize]<markMin){ 62 queue1[i]=queue1[nowQueueSize]; 63 break; 64 }else{ 65 queue1[i]=markMin; 66 i=markI; 67 } 68 } 69 } 70 nowQueueSize--; 71 return mark; 72 } 73 public static void main(String[] args) throws Exception { 74 PriorityQueue1 queueTest=new PriorityQueue1(); 75 queueTest.push(2); 76 queueTest.push(4); 77 queueTest.push(3); 78 queueTest.push(1); 79 queueTest.push(6); 80 queueTest.push(5); 81 for(int i=1;i<=6;i++){ 82 System.out.print(queueTest.pop()+" "); 83 } 84 System.out.println(); 85 System.out.println(queueTest.pop()); 86 87 } 88 89 }
运行结果:
4 4 3 优先队列进行拓展一次空间 2 3 4 2 3 4 6 2 3 4 6 5 2 3 4 5 6 Exception in thread "main" java.lang.Exception: 优先队列已空,不能进行出队列操作! at Queue.PriorityQueue1.pop(PriorityQueue1.java:40) at Queue.PriorityQueue1.main(PriorityQueue1.java:87)
四、总结
其实堆也只是一种思想,思想上和数的结构很像,但是实现上我们可以有数组和链表实现,主要是了解这种思想。
关于的堆的合并操作,我找时间再补充吧!其实简单。