首先我们来讲讲什么是栈,主要是介绍我对栈的了解和认识:栈是一种用于存储数据的表,鲜明的特点是先进后出FILO,栈的实现分为数组实现和链表实现。学习栈看中学习栈的思想,通过栈的思想解决一些实际中的问题。Java中有Stack类实现栈的操作。这篇博客主要阐述,栈的基本实现,数组实现和链表实现。
一、栈的模型图
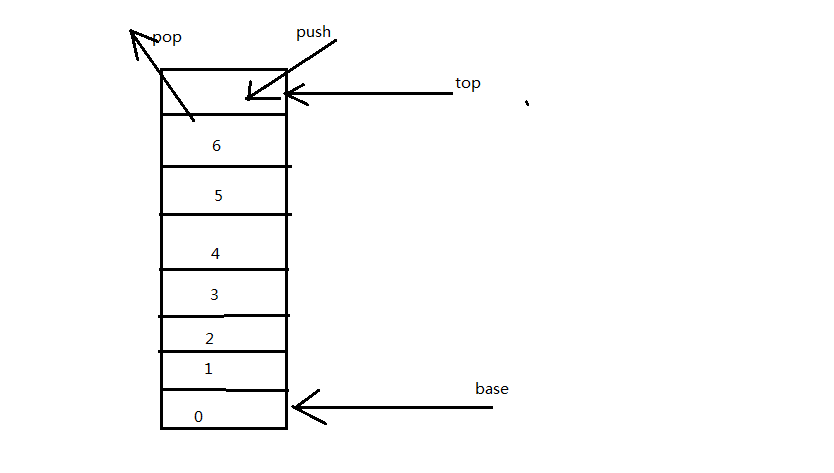
入栈的顺序为:0、1、2、3、 4、 5、6 出栈的顺序为6、5、4、3、2、1、0
二、栈的数组实现
这个栈的实现是通过数组实现的,通过动态的扩充数组的长度来实现无界栈。
代码实现:
1 package Stack; 2 3 public class Stack1 { 4 private int stack[];//用于存储栈内元素的数组 5 private int DEFAULTSIZE=5;//默认初始化栈的存储空间 6 private int top;//栈顶指针 7 private int base;//栈底指针 8 private int nowSize;//栈当前的元素个数 9 private int sumSizeFlag=1;//当前栈拓展的栈的空间为默认空间大小的倍数 10 //初始化栈,给栈分配内存,初始化一些参数 11 public Stack1() { 12 stack=new int[DEFAULTSIZE]; 13 top=0; 14 nowSize=0; 15 base=0; 16 } 17 //给栈进行拓展空间 18 private void enLargeSize(){ 19 int []mark=stack; 20 stack=new int[DEFAULTSIZE*sumSizeFlag]; 21 for(int i=0;i<nowSize;i++){ 22 stack[i]=mark[i]; 23 } 24 System.out.println("栈进行了一次存储空间的扩充!"); 25 } 26 //入栈操作 27 public void push(int m){ 28 if(nowSize==stack.length){ 29 sumSizeFlag++; 30 enLargeSize(); 31 } 32 stack[nowSize]=m; 33 nowSize++; 34 top++; 35 36 } 37 //出栈操作 38 public int pop() throws Exception{ 39 if(top==0) 40 throw new Exception("栈空,不能进行出栈操作!"); 41 top--; 42 int mark=stack[top]; 43 nowSize--; 44 return mark; 45 } 46 public static void main(String[] args) throws Exception { 47 Stack1 stack1=new Stack1(); 48 for(int i=0;i<6;i++){ 49 stack1.push(i); 50 } 51 52 for(int i=0;i<6;i++) 53 System.out.print(stack1.pop()+" "); 54 System.out.println(); 55 System.out.println(stack1.pop()); 56 } 57 }
运行结果:
1 栈进行了一次存储空间的扩充! 2 5 4 3 2 1 0 3 Exception in thread "main" java.lang.Exception: 栈空,不能进行出栈操作! 4 at Stack.Stack1.pop(Stack1.java:40) 5 at Stack.Stack1.main(Stack1.java:55)
三、栈的链表实现
这里链表实现栈的操作,需要设置两个(引用)指针,一个专门指向他的上一个节点,另一个指针专门指向它的下一个指针,链表实现栈其实在操作上还是听麻烦的,两个引用的设置还是得很小心的。所以相对于链表实现我跟喜欢数组实现。
代码实现:
1 //节点类 2 class Node{ 3 private int date;//存储数据 4 private Node next;//指向下一个节点 5 private Node prior;//指向上一个节点 6 public int getDate() { 7 return date; 8 } 9 public void setDate(int date) { 10 this.date = date; 11 } 12 public Node getNext() { 13 return next; 14 } 15 public void setNext(Node next) { 16 this.next = next; 17 } 18 public Node getPrior() { 19 return prior; 20 } 21 public void setPrior(Node prior) { 22 this.prior = prior; 23 } 24 25 } 26 public class Satck2 { 27 private Node top;//栈顶指针 28 private Node base;//栈底指针 29 private int nowSize;//栈当前的元素个数 30 //初始化栈,初始化一些参数 31 public Satck2() { 32 Node head=new Node(); 33 base=top=head; 34 nowSize=0; 35 head.setPrior(null); 36 head.setNext(null); 37 } 38 39 //入栈操作 40 public void push(int m){ 41 top.setDate(m); 42 top.setNext(new Node()); 43 top.getNext().setPrior(top);//这里需要帮助新创建的节点的prior指针指向前一个节点 44 top=top.getNext(); 45 nowSize++; 46 } 47 //出栈操作(出栈的时候相当于先获得栈顶指针的下一个元素的数据,将这个数据的节点删除) 48 public int pop() throws Exception{ 49 if(nowSize==0) 50 throw new Exception("栈空,没法进行出栈操作!"); 51 int mark=top.getPrior().getDate(); 52 if(top.getPrior().getPrior()!=null){ 53 top.getPrior().getPrior().setNext(top); 54 top.setPrior(top.getPrior().getPrior()); 55 }else if(top.getPrior().getPrior()==null){ 56 top.setNext(null); 57 top.setPrior(null); 58 } 59 nowSize--; 60 return mark; 61 } 62 63 public static void main(String[] args) throws Exception { 64 Satck2 stack1=new Satck2(); 65 for(int i=0;i<6;i++){ 66 stack1.push(i); 67 } 68 69 for(int i=0;i<6;i++) 70 System.out.print(stack1.pop()+" "); 71 System.out.println(); 72 System.out.println(stack1.pop()); 73 } 74 75 }
运行结果:
5 4 3 2 1 0 Exception in thread "main" java.lang.Exception: 栈空,没法进行出栈操作! at Stack.Satck2.pop(Satck2.java:51) at Stack.Satck2.main(Satck2.java:73)
三、通过栈思想实现的计算器(实现带括号的整数的加减乘除)
首先需要将中缀式通过栈转化为后缀式,然后使用后缀式通过栈计算算式的答案。
中缀式转化为后缀式的思想:建立一个stack,先对输入的字符串进行转化,转化成字符数组,遍历这个字符数组:
1、当遇到数字时候把他们按顺序存放在一个新的数组中,
2、当遇到符号时,先判断栈是否为空,为空直接进栈,否则判断是否栈中的元素的优先级是否比自己大,比自己大或相等,循环进行出栈操作,将出 栈的元素继续放在新的数组中,知道栈空或遇到栈中比自己优先级小的操作符,然后入栈。其中优先级顺序:'(' > '* '= '/' > '+' = '-' > ')' 。 这里必须强调一下当遇到‘)’则是一直出栈至‘(’为止。
后缀式计算算式答案的思想:建立一个stack,当遇到数字直接入入栈,当遇到符号,则先出栈两次,将两次出栈的数字进行进行相应的计算,然后将结果入栈,这样一直执行下 去,直到对数组遍历完成,然后出栈的结果即为答案。
例如:1*(1+2*3)+1
中缀式转为后缀式:
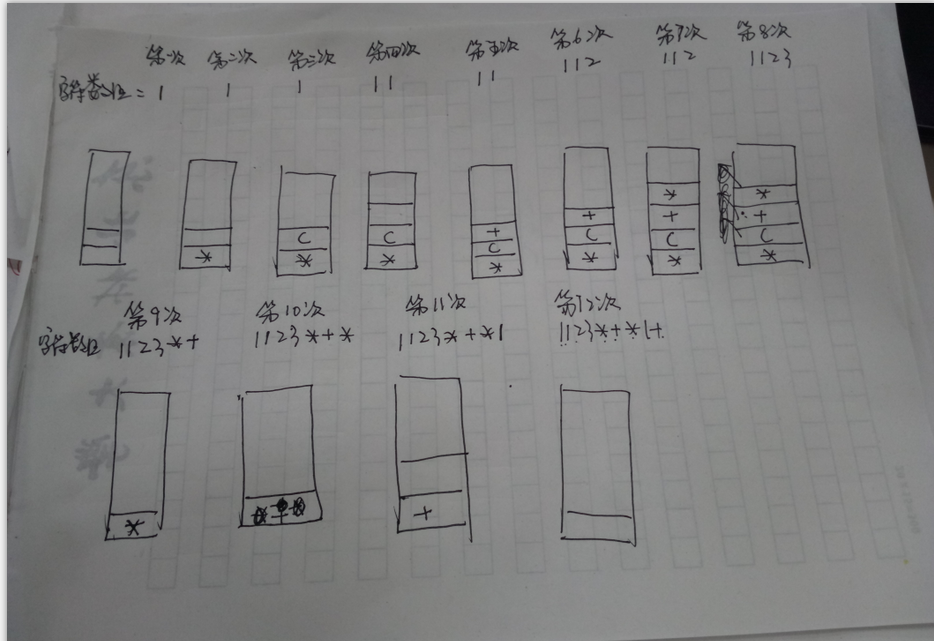
后缀式计算比较简单,这里就不画图了。。。
直接上代码:
1 package Stack; 2 3 import java.util.Scanner; 4 import java.util.Stack; 5 6 public class Calculator { 7 private int fixLength;//用于记录当前字符数组的元素个数 8 //将中缀式转化为后缀式 9 public String[] infixToPostfix(char []infix){ 10 String []st=new String[infix.length]; 11 Stack<Character> stack=new Stack<Character>(); 12 int nowLocationMark=0;//记录当前数组重新添加进去的元素个数 13 String str=""; 14 for(int i=0;i<infix.length;i++){ 15 //System.out.println(stack.size()); 16 if('0'<=infix[i]&&infix[i]<='9'){ 17 str=str+infix[i]; 18 if((i==infix.length-1)||('0'>infix[i+1]||infix[i+1]>'9')){ 19 st[nowLocationMark]=str; 20 str=""; 21 nowLocationMark++; 22 } 23 }else{ 24 if(stack.isEmpty()){ 25 stack.push(infix[i]); 26 }else{ 27 if(infix[i]=='('){ 28 stack.push(infix[i]); 29 }else if(infix[i]=='*'||infix[i]=='/'){ 30 if(stack.peek()=='*'||stack.peek()=='/'){ 31 while(!stack.isEmpty()&&(stack.peek()!='+'&&stack.peek()!='-')){ 32 str=str+stack.pop(); 33 st[nowLocationMark]=str; 34 str=""; 35 nowLocationMark++; 36 } 37 } 38 stack.push(infix[i]); 39 }else if(infix[i]==')'){ 40 char mark; 41 mark=stack.pop(); 42 do{ 43 44 str=str+mark; 45 mark=stack.pop(); 46 st[nowLocationMark]=str; 47 str=""; 48 nowLocationMark++; 49 }while(mark!='('); 50 //stack.pop();//这里讲'('从数组中删除 51 //fixLength=fixLength-2;//这里也需要知道字符数组的长度减小了2 52 }else if(infix[i]=='+'||infix[i]=='-'){ 53 if(stack.peek()=='+'||stack.peek()=='-'||stack.peek()=='*'||stack.peek()=='/'){ 54 while(!stack.isEmpty()&&stack.peek()!='('){ 55 str=str+stack.pop(); 56 st[nowLocationMark]=str; 57 str=""; 58 nowLocationMark++; 59 } 60 } 61 stack.push(infix[i]); 62 } 63 } 64 } 65 } 66 //将栈中还没输出的元素出栈操作 67 while(!stack.isEmpty()){ 68 str=str+stack.pop(); 69 st[nowLocationMark]=str; 70 str=""; 71 nowLocationMark++; 72 } 73 fixLength=nowLocationMark;//将当前字符数组的元素个数记录下来 74 return st; 75 } 76 //用于对后缀表达式进行处理,最后计算出一个答案 77 public int doPostfix(String []postfix){ 78 //System.out.println(fixLength); 79 double mark; 80 Stack<Integer> stack=new Stack<Integer>(); 81 for(int i=0;i<fixLength;i++){ 82 if(postfix[i].equals("*")||postfix[i].equals("/")||postfix[i].equals("+")||postfix[i].equals("-")){ 83 int mark1=stack.pop(); 84 int mark2=stack.pop(); 85 System.out.println(mark1+postfix[i]+mark2); 86 switch (postfix[i]) { 87 case "*": 88 stack.push(mark1*mark2); 89 break; 90 case "/": 91 stack.push(mark2/mark1); 92 break; 93 case "+": 94 stack.push(mark2+mark1); 95 break; 96 case "-": 97 stack.push(mark2-mark1); 98 break; 99 } 100 }else{ 101 stack.push(Integer.parseInt(postfix[i])); 102 } 103 } 104 105 return stack.pop(); 106 } 107 //计算器启动方法 108 public void startCalculator(){ 109 Scanner sc=new Scanner(System.in); 110 while(sc.hasNext()){ 111 //sc.nextLine(); 112 String str=sc.nextLine(); 113 char []fix=str.toCharArray(); 114 System.out.println(doPostfix(infixToPostfix(fix))); 115 } 116 } 117 public static void main(String[] args) { 118 Calculator calculator=new Calculator(); 119 calculator.startCalculator(); 120 //之前用于测试的代码 121 /*char []ch={'1','+','(','1','+','2','*','3','1',')','*','2','/','2'}; 122 String[] s=calculator.infixToPostfix(ch); 123 for(int i=0;i<s.length;i++){ 124 System.out.print(s[i]); 125 } 126 System.out.println(calculator.doPostfix(s));*/ 127 } 128 129 }
运行结果:
1+3*(1+2+3*4)+1 2+1 4*3 12+3 15*3 45+1 1+46 47
注:第一行为输入,第二行到第七行为运算过程,第八航为结果。
这个计算器的代码想的比较简单,可能有的可能没考虑到,只能进行带括号的加减乘除运算,甚至还不能进行浮数计算,以简单为主,主要思想就是通过栈的思想来实现计算器,主要是验证栈思想。