java二叉查找树实现:
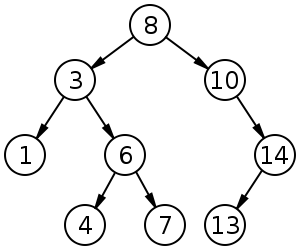
二叉查找树,上图:比根节点小者在其左边,比根节点大者在其右边。
抽象数据结构,上代码:
/** * 二叉查找树数据结构(非线程安全): * 范型类型须实现Comparable接口,用于比较操作 */ public class BinarySearchTree<T extends Comparable<T>> { private Node<T> root; // tree root private int count; // tree element counts /** * 内部节点类 */ private static class Node<E>{ E value; //元素对象 Node<E> parent; //父节点 Node<E> left; //左孩子节点 Node<E> right; //右孩子节点 public Node(E value, Node<E> parent, Node<E> left, Node<E> right) { this.value = value; this.parent = parent; this.left = left; this.right = right; } } }
一些基本操作实现:
- 插入(insert): 依次比较根元素,小者放左边,大者放右边:
/** * 插入元素 * @param t 待插入元素 * @return 插入成功返回true, 反之返回false */ public boolean insert(T t){ if (root == null){ //若为空树 root = new Node<T>(t, null, null, null); return true; } Node<T> newNode = new Node<T>(t, null, null, null); Node<T> pointer = root; while(true){ if (newNode.value.compareTo(pointer.value) > 0){ if (pointer.right == null){ //插入右边 newNode.parent = pointer; pointer.right = newNode; count++; return true; } else{ pointer = pointer.right; } } else if (newNode.value.compareTo(pointer.value) < 0){ if (pointer.left == null){ //插入左边 newNode.parent = pointer; pointer.left = newNode; count++; return true; } else{ pointer = pointer.left; } } else { //相等了 return false; } } }
- 查找(get):
/** * 查找元素 * @param t 待查找元素 * @return 对应元素或null */ public T get(T t) { Node<T> n = getN(t); return n == null? null : n.value; } /** * 查找节点 * @param t 待查找元素 * @return 元素对应节点或null */ private Node<T> getN(T t) { Node<T> cur = root; while (cur != null){ if (cur.value.compareTo(t) < 0){ //右边子树找 cur = cur.right; } else if(cur.value.compareTo(t) > 0){ //左边子树找 cur = cur.left; } else{ //找到该节点 break; } } return cur; }
- 查找最大,最小元素:
/** * 获取某节点为根的树的最小元素 */ public T min(Node<T> n){ Node<T> min = minN(n); return min == null ? null : min.value; } /** * 获取某节点为根的树的最小节点 * @param n 树根节点 * @return 该子树最小节点 */ private Node<T> minN(Node<T> n){ Node<T> min = n; while (min != null && min.left != null){ min = min.left; } return min; } /** * 获取某节点为根的树的最大元素 * @return 最大元素, 没有返回null */ public T max(Node<T> n){ Node<T> max = maxN(n); return max == null ? null : max.value; } /** * 获取某节点为根的树的最大节点 */ private Node<T> maxN(Node<T> n){ Node<T> max = n; while (max != null && max.right != null){ max = max.right; } return max; }
- 遍历树(中序遍历):
/** * 中序遍历 */ public void leftRootRight(){ printLRR(root); } /** * 中序遍历打印元素 */ private void printLRR(Node<T> node) { if (node != null){ printLRR(node.left); System.out.println(node.value); printLRR(node.right); } }
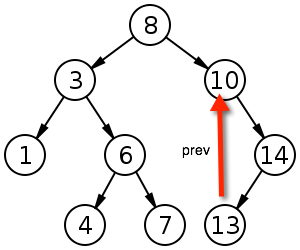
- 获取前驱(prev)元素:
主要有两种情况:
1.该节点左子树不为空:其前驱节点为其左子树的最大元素:
2.该节点左子树为空: 其前驱节点为其祖先节点(递归),且该祖先节点的右孩子也为其祖先节点(就是一直往其parent找,出现左拐后的那个祖先节点):
代码实现:
/** * 获取元素前驱(中序遍历) * @param t 指定元素 * @return 元素前驱,没有返回null */ public T prev(T t){ //先找到该元素 Node<T> cur = getN(t); if (cur != null){ return locatePrev(cur); } return null; } /** * 定位到前驱节点 * @param cur 当前节点 * @return 前驱节点,没有返回null */ private T locatePrev(Node<T> cur) { Node<T> prev = locatePrevN(cur); return prev == null ? null : prev.value; } /** * 定位到前驱节点 * @param cur 当前节点 * @return 当前节点的前驱节点 */ private Node<T> locatePrevN(Node<T> cur){ if (cur != null){ //1.如果该节点左子树不会空,则其前驱为其左子树的最大元素 if (cur.left != null) return maxN(cur.left); //2.该节点左子树为空, 则其前驱为:其祖先节点(递归), 且该祖先节点的右孩子也是其祖先节点 // 通俗的说,一直忘上找找到左拐后那个节点; Node<T> p = cur.parent; while(p != null && cur == p.left){ cur = p; p = p.parent; } return p == null ? null: p; } return null; }
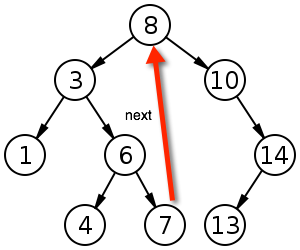
- 获取后继节点,也分两种情况:
1.该节点右子树不为空,其后继节点为其右子树的最小元素:
2.该节点右子树为空,其后继节点为其祖先节点(递归),且此祖先节点的左孩子也是该节点的祖先节点,就是说一直往上找其祖先节点,直到出现右拐后的那个祖先节点:
实现代码:
/** * 获取元素后继元素(中序遍历) * @param t 指定元素 * @return 后继元素,没有返回null */ public T next(T t){ //先找到该元素 Node<T> cur = getN(t); if (cur != null){ return locateNext(cur); } return null; } /** * 定位当前节点的后继元素 * @param cur 当前节点 * @return 其后继元素 */ private T locateNext(Node<T> cur) { Node<T> next = locateNextN(cur); return next == null ? null : next.value; } /** * 定位到当前节点的后继节点 * @param cur 当前节点 * @return 当前节点的后继节点 */ private Node<T> locateNextN(Node<T> cur) { if (cur == null) return null; //1.若其右子树不为空,那么其后继节点就是其右子树的最小元素 if (cur.right != null) return minN(cur.right); //2.若为空,应该为其祖先节点(递归),且该祖先节点的左孩子也是其祖先节点 // 通俗的说,一直忘上找,找到右拐后那个节点; Node<T> p = cur.parent; while (p != null && cur == p.right){ cur = p; p = p.parent; } return p; }
删除(remove), 可分为三种情况:
1.该节点为叶子节点,直接删除:
2.该节点有一个孩子,将其孩子接上其父节点:
3.该节点有2个孩子,先删除其右子树的最小元素(该元素最多只会有一个孩子),将这个最小元素去替换要删除的节点:
实现代码:
/** * 移除某元素 * @param t 待删除元素 * @return 删除成功返回true, 反之false */ public boolean remove(T t){ //找到该节点 Node<T> cur = getN(t); if (cur != null){ if (doRemove(cur)){ cur=null; count--; return true; } } return false; } /** * 执行删除操作 */ private boolean doRemove(Node<T> cur) { //该节点是否为根 boolean isRoot = cur == root; //1.该节点为叶子节点, 直接将其父节点对应(左或右)孩子置空 if (cur.left == null && cur.right == null){ if (isRoot) return true; //若树只有一个根节点 if (cur == cur.parent.right) //该节点为父节点的右孩子 cur.parent.right = null; else //该节点为父节点的左孩子 cur.parent.left = null; return true; } else if(cur.left != null && cur.right != null){ //2.该节点有2个孩子, 我们先找出一个替换节点(该节点的后继节点,后继节点没有则前驱节点) //找到其后继节点 Node<T> replaceNode = locateNextN(cur); if (replaceNode == null) //若没有后继节点则用前驱节点 replaceNode = locatePrevN(cur); doRemove(replaceNode); cur.value = replaceNode.value; return true; } else{ //3.该节点有1个孩子, 直接将其父节点对应(左或右)孩子接到其非空孩子 Node<T> needLinkedNode = null; if (cur.left == null && cur.right != null){ //该节点有右孩子 needLinkedNode = cur.right; } else if(cur.left != null && cur.right == null){ //该节点有左孩子 needLinkedNode = cur.left; } if(isRoot){ //若该节点为根 root = needLinkedNode; return true; } if (cur == cur.parent.right) //该节点为父节点右孩子 cur.parent.right = needLinkedNode; else cur.parent.left = needLinkedNode; return true; } }