三 图的遍历
遍历定义:从已给的连通图中某一顶点出发,沿着一些边访遍图中所有的顶点,且使每个顶点仅被访问一次,就叫做图的遍历,它是图的基本运算。
避免重复访问?
图中可能存在回路,且图的任一顶点都可能与其它顶点相通,在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的顶点。为了保证图中的各个顶点在遍历过程中访问且仅被访问一次,需要为每个顶点设一个访问标志,Vertex 类中的visited成员变量可以用来作为是否被访问过的标志。
3.1深度优先搜索( DFS )Depth First Search
深度优先搜索(depth firstsearch)遍历类似于树的先根遍历,是树的先根遍历的推广。
深度优先搜索的基本方法是:从图中某个顶点发v 出发,访问此顶点,然后依次从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
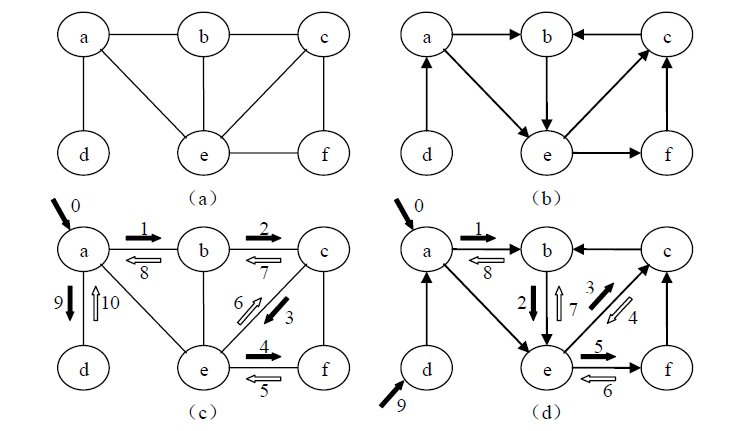
无向图(a)得到的遍历序列为:a , b ,c , e , f , d。
有向图(b)得到的遍历序列为:a , b ,e , c , f , d。
//对图进行深度优先遍历
public Iterator DFSTraverse(Vertex v) {
LinkedList traverseSeq = new LinkedListDLNode();//遍历结果
resetVexStatus(); //重置顶点状态
DFSRecursion(v, traverseSeq); //从v点出发深度优先搜索
Iterator it = getVertex(); //从图中未曾访问的其他顶点出发重新搜索
for(it.first(); !it.isDone(); it.next()){
Vertex u = (Vertex)it.currentItem();
if (!u.isVisited()) DFSRecursion(u, traverseSeq);
}
return traverseSeq.elements();
}
3.1.1 DFSTraverse递归实现
//深度优先的递归算法
private void DFSRecursion(Vertex v, LinkedList list){
v.setToVisited();
list.insertLast(v);
Iterator it = adjVertexs(v);//取得顶点v的所有邻接点
for(it.first(); !it.isDone(); it.next()){
Vertex u = (Vertex)it.currentItem();
if (!u.isVisited()) DFSRecursion(u,list);
}
}
3.1.2使用堆栈以非递归的形式实现
图的深度优先搜索算法也可以使用堆栈以非递归的形式实现,使用堆栈实现深度优先搜索的思想如下:
⑴ 首先将初始顶点v入栈;
⑵ 当堆栈不为空时,重复以下处理
栈顶元素出栈,若未访问,则访问之并设置访问标志,将其未曾访问的邻接点入栈;
⑶ 如果图中还有未曾访问的邻接点,选择一个重复以上过程。
算法DFS的非递归实现
//深度优先的非递归算法
private void DFS(Vertex v, LinkedList list){
Stack s = new StackSLinked();
s.push(v);
while (!s.isEmpty()){
Vertex u = (Vertex)s.pop();
if (!u.isVisited()){
u.setToVisited();
list.insertLast(u);
Iterator it = adjVertexs(u);
for(it.first(); !it.isDone(); it.next()){
Vertex adj = (Vertex)it.currentItem();
if (!adj.isVisited()) s.push(adj);
}
}//if
}//while
}
3.2广度优先搜索( BFS )Breadth First Search
广度优先搜索(breadth firstsearch) 遍历类似于树的层次遍历,它是树的按层遍历的推广。
假设从图中某顶点v 出发,在访问了v 之后依次访问v 的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”先被访问,直至图中所有已被访问的顶点的邻接点都被访问到。若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
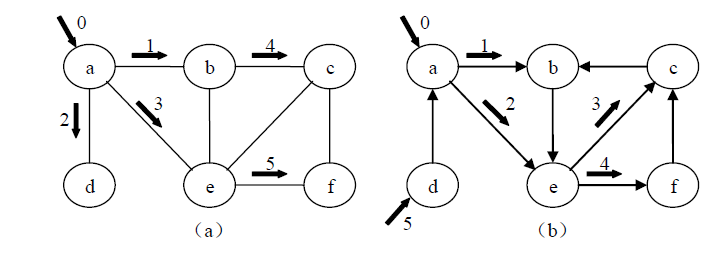
图(a)中无向图的广度优先搜索遍历序列为:a , b , d , e , c , f;
图(b)中有向图的广度优先搜索遍历序列为:a , b , e , c , f , d。
通过上述搜索过程,我们发现,广度优先搜索遍历图的过程实际上就是以起始点v 为起点,由近至远,依次访问从v 出发可达并且路径长度为1、2、…的顶点。
广度优先搜索遍历的实现与树的按层遍历实现一样都需要使用队列,使用队列实现广度优先搜索的思想如下:
① 首先访问初始顶点v 并入队;
② 当队列不为空时,重复以下处理
队首元素出队,访问其所有未曾访问的邻接点,并它们入队;
③ 如果图中还有未曾访问的邻接点,选择一个重复以上过程。
广度优先遍历BFSTraverse
//对图进行广度优先遍历
public Iterator BFSTraverse(Vertex v) {
LinkedList traverseSeq = new LinkedListDLNode();//遍历结果
resetVexStatus(); //重置顶点状态
BFS(v, traverseSeq); //从v点出发广度优先搜索
Iterator it = getVertex(); //从图中未曾访问的其他顶点出发重新搜索
for(it.first(); !it.isDone(); it.next()){
Vertex u = (Vertex)it.currentItem();
if (!u.isVisited()) BFS(u, traverseSeq);
}
return traverseSeq.elements();
}
private void BFS(Vertex v, LinkedList list){
Queue q = new QueueSLinked();
v.setToVisited();
list.insertLast(v);
q.enqueue(v);
while (!q.isEmpty()){
Vertex u = (Vertex)q.dequeue();
Iterator it = adjVertexs(u);
for(it.first(); !it.isDone(); it.next()){
Vertex adj = (Vertex)it.currentItem();
if (!adj.isVisited()){
adj.setToVisited();
list.insertLast(adj);
q.enqueue(adj);
}//if
}//for
}//while
}