数据结构>图的最短路径 小强斋

六、最短路径

典型用途：交通问题。如：城市A到城市B有多条线路，但每条线路的交通费（或所需时间）不同，那么，如何选择一条线路，使总费用（或总时间）最少？

问题抽象：在带权有向图中A点（源点）到达B点（终点）的多条路径中，寻找一条各边权值之和最小的路径，即最短路径。

两种常见的最短路径问题：一顶点到其余各顶点、任意两顶点之间

6.1、单源最短路径—--用Dijkstra（迪杰斯特拉）算法

设一有向图G=(V,E)，已知各边的权值，以某指定点v₀为源点，求从v₀到图的其余各点的最短路径。限定各边上的权值大于或等于0。

设置辅助数组Dist，其中每个分量Dist[k] 表示 当前所求得的从源点到其余各顶点 k 的最短路径。

一般情况下，Dist[k]= <源点到顶点 k的弧上的权值>

或者  = <源点到其它顶点的路径长度>+<其它顶点到顶点 k的弧上的权值>

即它或者是直接从源点到该点(只含一条弧)； 或者是从源点经过已求得最短路径的顶点，再到达该顶点。

迪杰斯特拉(Dijkstra)算法思想

按路径长度递增次序产生最短路径算法：

把V分成两组：

   (1) S：已求出最短路径的顶点的集合

   (2) V-S=T：尚未确定最短路径的顶点集合

将T中顶点按最短路径递增的次序加入到S中，保证

   (1) 从源点V0到S中各顶点的最短路径长度都不大于从V0到T中任何顶点的最短路径长度

   (2) 每个顶点对应一个距离值

         S中顶点：从V0到此顶点的最短路径长度

         T中顶点：从V0到此顶点的只包括S中顶点作中间顶点的最短路径长度

算法描述：

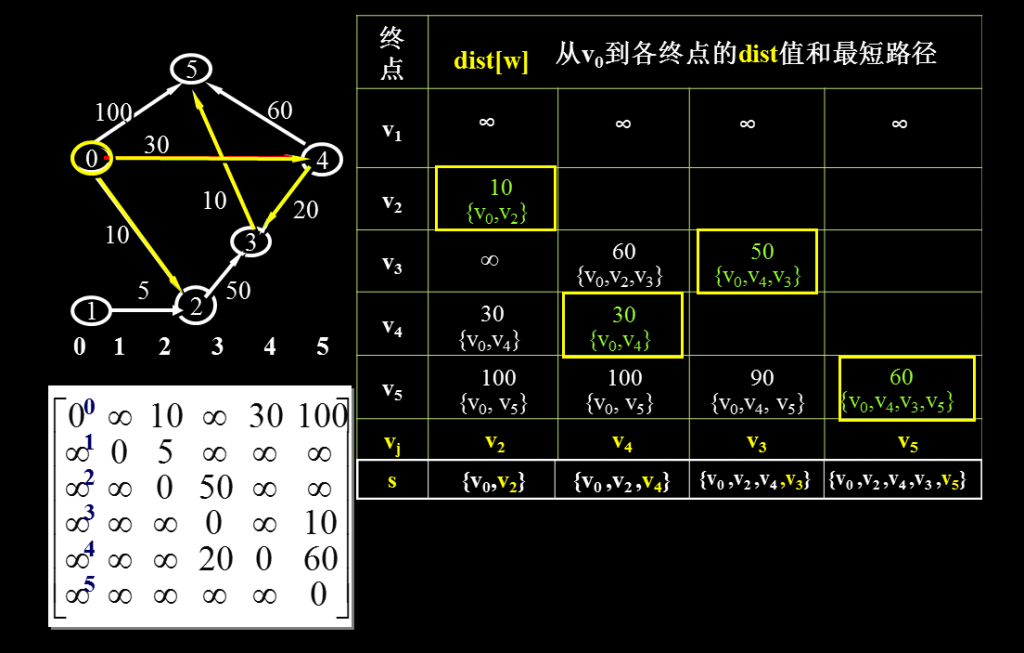
（1）设A[n][n]为有向网的带权邻接矩阵，A[i][j]表示弧（vi，vj )的权值，S为已找到从源点v0出发的最短路径的终点集合，它的初始状态为{v0}.辅助数组dist[n]为各终点当前找到的最短路径的长度，它的初始值为 dist[i]＝A[v0,i] 即邻接矩阵中第v0行的权值

（2）选择u，使得 dist[u]＝min{dist[w]|w∈V-S } ，即dist[u]是从源点v0到S集外所有顶点的弧中最短的一条,其中w是S集之外的顶点，将u加入S集  S=S∪{u}

（3）对于所有不在S中的终点w，若

     dist[u]+ A[u,w]< dist[w] ，即(v0,u)＋(u,w)<(v0,w)

     则修改dist[w]为： dist[w]＝dist[u]+ A[u,w]

（4）重复操作（2）、（3）共n-1次，由此求得从v0到各终点的最短路径。

Dijkstra算法求单源最短路径：

设 V 是该有向图的结点的集合、集合 S 是已求得最短路径的结点的集合, 求 V0 至其余各结点的最短距离。

1、S ＝  { 0 } ；// 结点 V0 最短路径已求得

2、for (  i=1; i<n; i++  )

3、{  D[i]=c[0][i];  P[v]=0; }

4、for (  i=1; i<n; i++  )

5、{  在V-S中选择一个结点VW；使得

          D[w] 最小。将W 加入集合S

6、    for (每一个在V-S中的结点V) {

6.5          if   (D[w]+C[w][v]<D[v])  P[v] =  w;

7、         D[v]=MIN(D[v],D[w]+C[w][v])

8        };

8、}

6.2、所有顶点间的最短路径—--用Floyd（弗洛伊德）算法

问题的提出：已知一个各边权值均大于0的带权有向图，对每一对顶点 v_i¹v_j，希望求出v_i与v_j之间的最短路径和最短路径长度。

解决思路：可以通过调用n次Dijkstra算法来完成，但时间复杂度为O(n³)。

改进： 弗洛伊德(Floyd)算法

算法思想：逐个顶点试探法

求最短路径步骤

1、初始时设置一个n阶方阵，令其对角线元素为0，若存在弧<V_i,V_j>，则对应元素为权值；否则为µ

2、逐步试着在原直接路径中增加中间顶点，若加入中间点后路径变短，则修改之；否则，维持原值

3、所有顶点试探完毕，算法结束

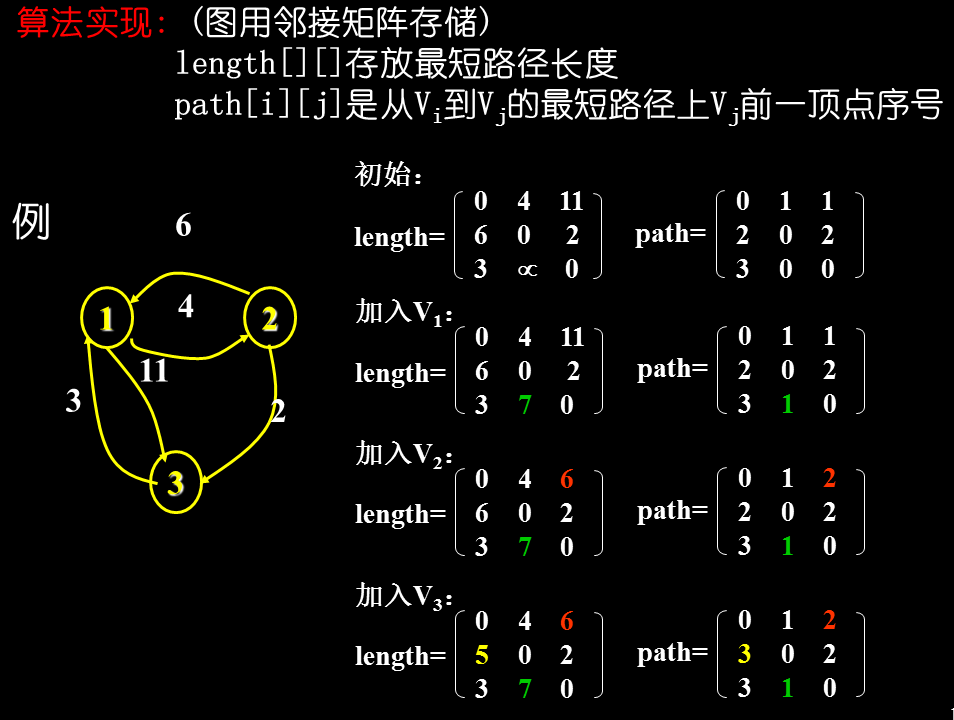
例子

Floyd 算法的程序的简单描述：

      int  i, j,k;  // 标识结点

      for (i=0; i<n; i++)

           for (j=0; j<n; j++) A[i,j] = C[i,j];

      for (i=0; i<n; i++ ) A[i,i] = 0;

      for (k=0; k<n; k++)

            for (i=0; i<n; i++)

                for (j=0; j<n; j++)

          if (A[i,k]+A[k,j]<A[i,j])

              A[i,j]=A[i,k]+A[k,j];