Codeforces Round #670 (Div. 2)/1406C Link Cut Centroids

题目链接：https://codeforces.com/contest/1406/problem/C

题目大意：对一棵树删去一条边，加上一条边，使树只保留一个重心

题目思路：树的重心是：删除这个点后最大连通块的结点数最小。以样例为例：

删除点1，点3为一个连通块，结点数为1，点2,4,5,为一个连通块，结点数为3 删除点2，点1,4,6分别为一个连通块，结点都是1 删除点3，点1,2,4,5为一个连通块，结点为4…………………… 这些点中，只有删除点2，才能使最大连通块的结点数最小，所以2为该树重心

如上步骤，发现点2，点3都是重心，这里需要知道树最多有2个重心

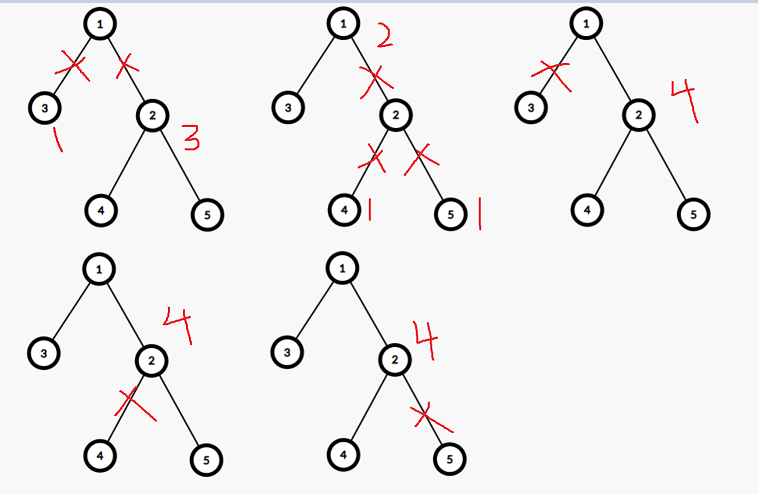
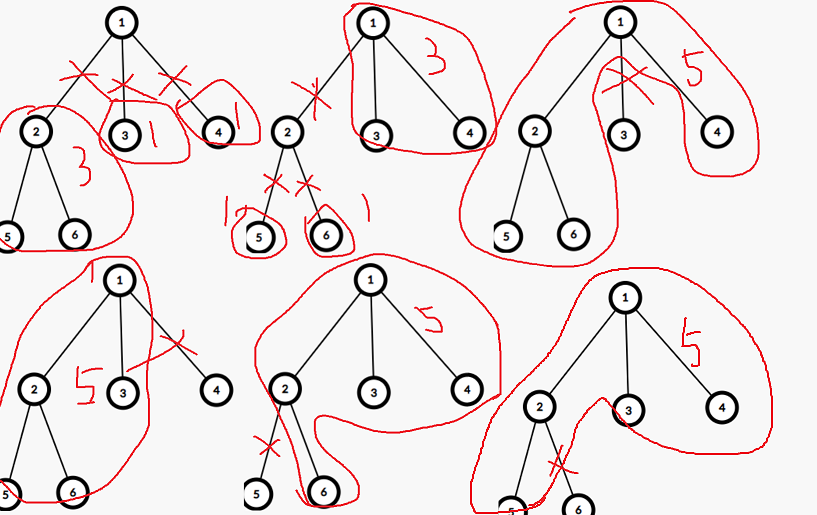
如果只有一个重心，那便删除、加上重心的任意一条边（删除加上是同一条），否则删除第2个重心的任意一条边（不能是与第1个重心相连的边，否则树还是有2个重心），然后将该边与第1个重心相连

接下来就是如何求重心了，我们知道树的重心是：删除这个点后最大连通块的结点数最小，所以我们对每个点求删除该点后最大联通块的最小值，首先通过dfs递归求出该点每个子树的最大连通块的数量，（同时对该点所有结点数求和，即1 + 该点所有子树的结点数，1为该点），然后与 `n - sum` 比较，求出该点的最大连通块的值

AC代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <map>
#include <string>
#include <cstring>
#include <set>
#include <stack>
#include <deque>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
typedef unsigned long long ull;
const int INF = 0x3f3f3f3f;
const int N = 1e6 + 10, M = 1e6 + 10;
const int base = 1e9;
const int P = 131;
const int MAX = 1e5;
int n, m, min_v = INF;
int h[N], e[M], ne[M], idx;
int son[N], siz[N];
bool st[N];
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dfs(int u)
{
    st[u] = true;
    int sum = 1, res = 0;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])//子节点未遍历过才加
        {
            siz[j] = dfs(j);//求子树的结点数
            res = max(res, siz[j]);//求子树中最大连通块的数量
            sum += siz[j];//对该点的结点求和
        }
    }
    res = max(res, n - sum);//n-sum为除掉子树的连通块的数量
    son[u] = res;
    min_v = min(min_v, son[u]);//计算最大联通块的最小值
    return sum;//返回子树的结点的和
}
int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
    {
        idx = 0, min_v = INF;
        scanf("%d", &n);
        for (int i = 1; i <= n; ++i)
            h[i] = -1;
        for (int i = 1; i <= n; ++i)
            st[i] = 0;
        for (int i = 1; i <= n - 1; ++i)
        {
            int a, b;
            scanf("%d%d", &a, &b);
            add(a, b), add(b, a);
        }
        dfs(1);
        int pos = 0, x1 = 0, x2 = 0;
        for (int i = 1; i <= n; ++i)//遍历找重心
        {
            if (son[i] == min_v)
            {
                if (x1 == 0)
                {
                    x1 = i;
                    ++pos;
                }
                else if (x2 == 0)
                {
                    x2 = i;
                    ++pos;
                    break;
                }
            }
        }
        if (pos == 1)//一个重心
        {
            int j = e[h[x1]];
            printf("%d %d\n", x1, j);
            printf("%d %d\n", x1, j);
        }
        else//两个重心
        {
            int j = 0;
            for (int i = h[x2]; i != -1; i = ne[i])
            {
                if (e[i] != x1)//不能是第1，2重心相连的边
                    j = e[i];
            }
            printf("%d %d\n", x2, j);
            printf("%d %d\n", x1, j);
        }
    }
    return 0;
}