https://undergroundmathematics.org/?tdsourcetag=s_pcqq_aiomsg
数学建模工具
1 Octave
2 Matlab
高数
第一章 函数、极限和连续
1 函数
单调增加
单调减少
2 极限
直接代入法
两个重要极限
解决诸如0/0、∞/∞、0x∞、∞-∞等问题使用洛必达法则
3 函数连续性
第二章 一元函数微分学
1 导数及微分的概念
2 导数及微分的计算
3 利用四则运算法则求导(必会)
4 复合函数的求导
5 二阶导数和高阶导数
6 求曲线在某点的切线方程或斜率
7 函数的特性(重要)
第三章 一元函数积分学
1 基本积分公式
2 换元积分法(常用的凑积分公式)
3 分部积分法
4 定积分
1 对称区间的定积分
2 变上限定积分
3 定积分计算
4 平面图形面积及旋转体体积
第四章 多元函数微分学
1 偏导的求法
2 全微分的求法
3 隐函数导数、偏导的求法
4 二阶偏导的求法
5 二元函数无条件极值的求法
6 二元函数条件极值的求法
高数(全)

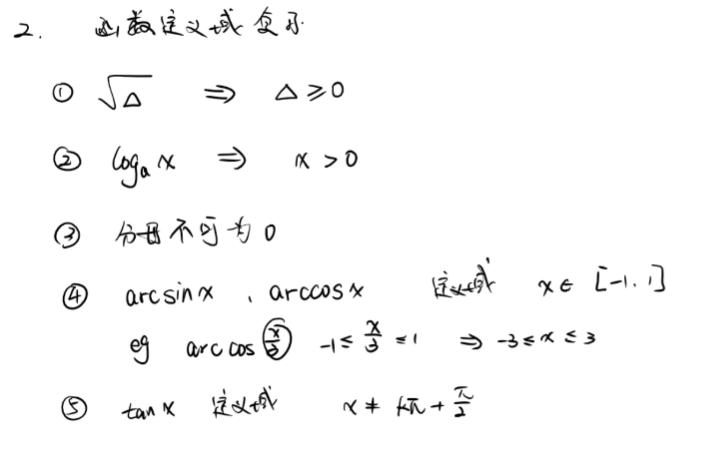

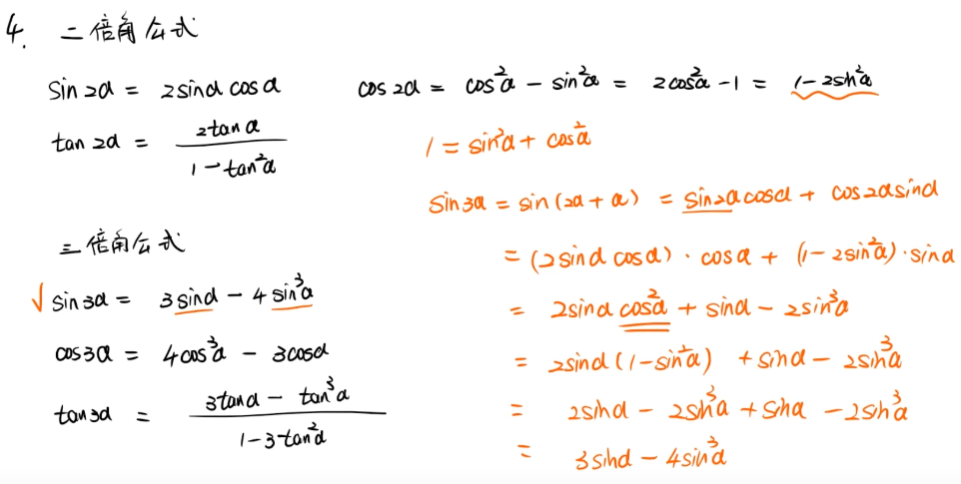
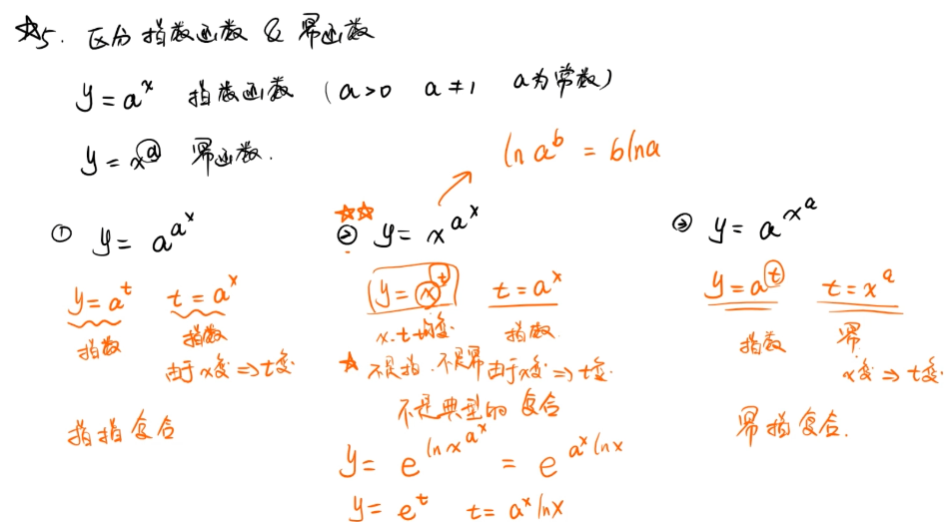
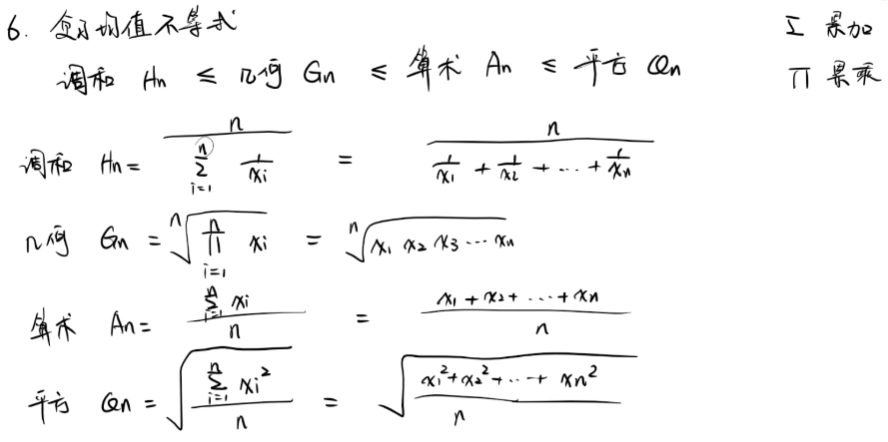


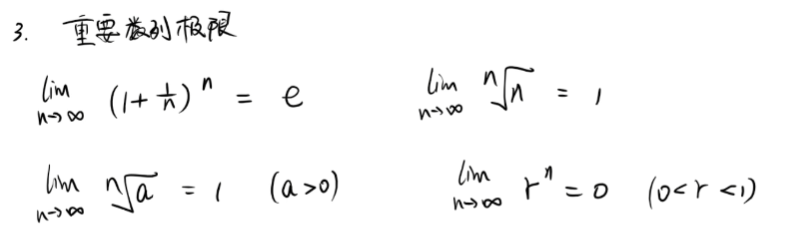
其他
提取公因式法
1
x^2-4x=0
x(x-4)=0
x=0,x-4=0
x=0 或 4
2
x(x-1)=6(x-1)
x(x-1)-6(x-1)=0
(x-6)(x-1)=0
x-6=0 或 x-1=0
x=6 或 x=1
去根号法则
√9=3
(√9)^2=9
(√a)^2=a
(√1/5)^2=1/5
√(-3)^2=|-3|=3 //开根号一定是非负的
√a^2=|a|
√(1/5)^2=|1/5|=1/5
√(-0.1)^2=|-0.1|=0.1
例:
√(-3)^2 + (√3)^2
= |-3| + 3
=3 + 3
=6