1.逻辑回归是怎么防止过拟合的?为什么正则化可以防止过拟合?(大家用自己的话介绍下)
在思考逻辑回归是如何防止过拟合的,首先了解一下什么是过拟合。
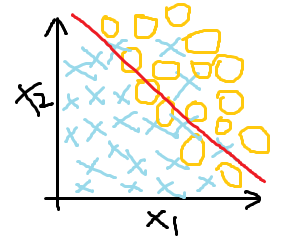
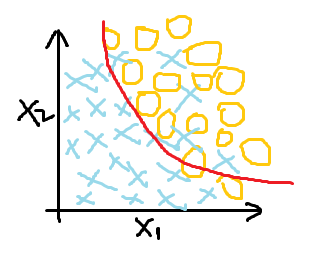
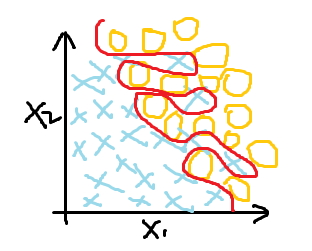
欠拟合(高偏差) 最好的拟合效果 过拟合(为了分类效果好,曲线过度曲折)
很明显,过拟合虽然达到了最好的分类效果,但在解决问题时并不实际,这时就需要找到过拟合产生的原因,针对性解决过拟合问题。
过拟合产生的原因是数据量太少,同时变量又比较多,虽然能够拟合所有的数据,但是造成了分类的曲线过度曲折。
既然是因为变量过多导致的,那么第一个想法就是将无用的变量去除,这就遇到下一个问题,什么样的变量才是无用变量,在我们无法判断什么变量是无用变量时,去除变量这种做法显然过于莽撞。于是就有了引进公式处理的方法,这就是正则化处理。
什么是正则化处理呢?
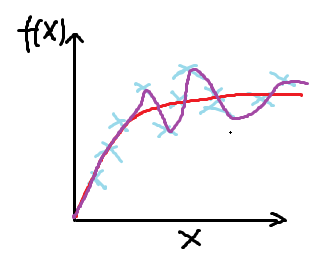
 θ0 + θ1x + θ2x2
θ0 + θ1x + θ2x2  θ0 + θ1x + θ2x2 + θ3x3 + θ4x4
θ0 + θ1x + θ2x2 + θ3x3 + θ4x4
在θ0 + θ1x + θ2x2 + θ3x3 + θ4x4 中,当 θ3、θ4足够小时, θ3x3 、θ4x4 可以忽略不计,函数十分接近二次方程。也就是说,θi 的减小使函数变得简单,但是我们并不知道哪些特征的参数应该减小,哪些特征时无用特征,因此引进了变量λ,同时缩小所有参数(θ1、θ2 、θ3……)。约定熟成,θ0作为最大值,并未接受任何的惩罚。

λ值过大会导致产生非常大的惩罚θ1、θ2 、θ3…θn,θ1 ≈ 0,θ2 ≈ 0,θ3 ≈ 0时是一条直线,会导致欠拟合。因此,选择合适的λ值才能使得正则化效果较好。
为什么采用正则化处理是最好的方式呢?
因为正则化处理保留了所有的特征,是通过参数θ进行调整,不管特征有多少,都能保留其对于结果的影响。并且利用λ值平衡了拟合效果。
2.用logistic回归来进行实践操作,数据不限。
肿瘤预测
1 import pandas as pd 2 import numpy as np 3 4 ''' 5 导入肿瘤数据 6 ''' 7 columns = ['id', 'feature_1', 'feature_2', 'feature_3', 'feature_4', 'feature_5', 'feature_6', 'feature_7', 'feature_8', 'feature_9', 'label'] 8 data_cancer = pd.read_csv("./data/breast-cancer-wisconsin.csv", header=None, names=columns) 9 data_cancer.head() 10 ''' 11 数据预处理 12 ''' 13 # 查看数据类型 14 data_cancer.dtypes 15 # 将feature_6列出现的?用空值代替,并将其转换类型 16 data_cancer['feature_6'] = data_cancer['feature_6'].replace(to_replace='?', value=np.nan) 17 data_cancer = data_cancer.dropna() 18 data_cancer['feature_6'] = data_cancer['feature_6'].astype('int64') 19 ''' 20 切分数据集:训练集/测试集 21 ''' 22 from sklearn.model_selection import train_test_split 23 X_train, X_test, y_train, y_test = train_test_split(data_cancer.iloc[:, 1:10], data_cancer.iloc[:, 10], test_size=0.3) 24 ''' 25 数据标准化处理 26 ''' 27 from sklearn.preprocessing import StandardScaler 28 std = StandardScaler() 29 X_train = std.fit_transform(X_train) 30 X_test = std.fit_transform(X_test) 31 ''' 32 构建模型 33 ''' 34 from sklearn.linear_model import LogisticRegression 35 lg_model = LogisticRegression() 36 ''' 37 训练模型 38 ''' 39 lg_model.fit(X_train, y_train) 40 ''' 41 测试模型 42 ''' 43 from sklearn.metrics import classification_report 44 y_pre = lg_model.predict(X_test) 45 print("准确率为:", lg_model.score(X_test, y_test)) 46 print("召回率为:", classification_report(y_test, y_pre, labels=[2, 4], target_names=['良性', '恶性']))


银行机构客户定期存款购买预测
场景:某银行机构的直接营销活动数据。
目的:通过现有数据预测客户是否购买定期存款
1.导入数据文件
1 ''' 2 导入银行数据 3 ''' 4 import pandas as pd 5 6 data_bank = pd.read_csv("./data/bank_data/bank.csv", sep=';', encoding='utf-8') 7 print("原始数据集维度:", data_bank.shape) 8 print("原始数据集的数据字段: ", data_bank.columns)
数据集有4521行记录,17个属性,属性内容如下:
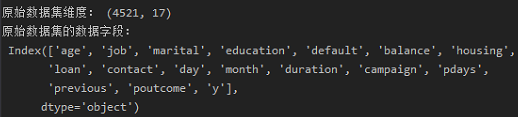

2.数据处理
1 ''' 2 数据预处理 3 ''' 4 # 查看数据类型 5 print("数据类型 ", data_bank.dtypes) 6 # 查看标签列 7 print("查看标签列: ", data_bank['y'].unique()) 8 # y列为标签列,将标签列转换为数值型 9 data_bank.loc[data_bank['y'] == 'yes', 'y'] = 1 10 data_bank.loc[data_bank['y'] == 'no', 'y'] = 0 11 # 查看两种类别的数量分布 12 print('两种类比的数量:', data_bank['y'].value_counts())


3.分析类别
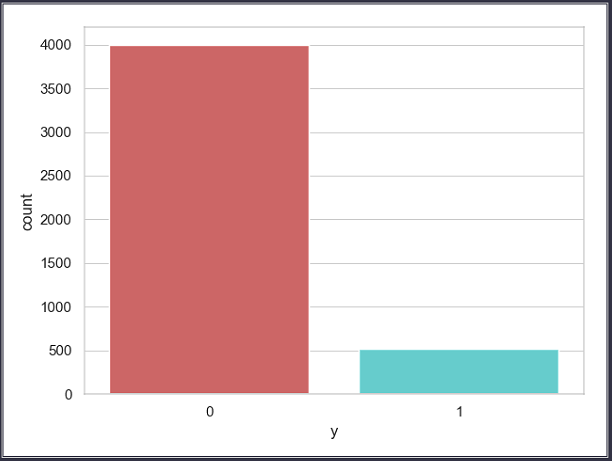
1 ''' 2 将标签类别数量通过柱形图展示出来 3 ''' 4 import matplotlib.pyplot as plt 5 import seaborn as sns 6 7 sns.set(style="white") 8 sns.set(style="whitegrid", color_codes=True) 9 sns.countplot(x='y', data=data_bank, palette='hls') 10 plt.show()
通过柱形图可以直观看出,两种类别的标签总数:
''' 分析两种类别 ''' data_bank.groupby('y').mean()
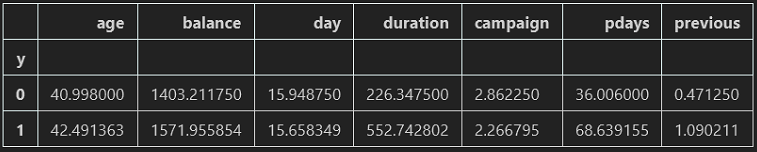
通过数据展示可以看出:
- 在银行购买定期存款的客户的平均年龄高于未购买定期存款的客户的平均年龄;
- 对于购买银行定期存款的客户来说,pdays(自上次银行联系客户以来的日子)值较低。也就说明了,pdays越低,客户对最后一次通话的记忆越好,销售的机会就越大;
- 购买银行定期存款的客户的广告系列(campaign当前广告系列期间与联系人通话次数)值较低。
为了能够更加详细了解数据,以及后续的模型构建及预测,对于数据集中的各个字段价值需要进行一定程度的分析,判断字段属性的舍取。
4.分析各种变量对于类别的影响(可视化展示)
1 ''' 2 可视化展示--job(工作职位)与y的关系 3 ''' 4 pd.crosstab(data_bank.job, data_bank.y).plot(kind='bar') 5 plt.title("工作不同的情况下购买存款的频率") 6 plt.xlabel("工作") 7 plt.ylabel("购买频率") 8 plt.show()

从上图可以看出,客户购买定期存款的频率很大程度上取决于其职业,因此,job是一个很好的预测因子。
1 ''' 2 可视化展示--marital(婚姻状况)与y的关系 3 ''' 4 tab = pd.crosstab(data_bank.marital, data_bank.y) 5 tab.div(tab.sum(axis=1).astype(float), axis=0).plot(kind='bar', stacked=True) 6 plt.title("婚姻状况与购买情况的堆积条形图") 7 plt.xlabel("婚姻状况") 8 plt.ylabel("客户比例") 9 plt.show()

由上图可以看出,婚姻状况对于客户是否购买定期存款影响不大,因此可以判断出婚姻状况似乎并不是预测因子。
1 ''' 2 可视化展示--education(教育)与y的关系 3 ''' 4 tab = pd.crosstab(data_bank.education, data_bank.y) 5 tab.div(tab.sum(axis=1).astype(float), axis=0).plot(kind='bar', stacked=True) 6 plt.title("受教育状况与购买情况的堆积条形图") 7 plt.xlabel("教育状况") 8 plt.ylabel("客户比例") 9 plt.show()
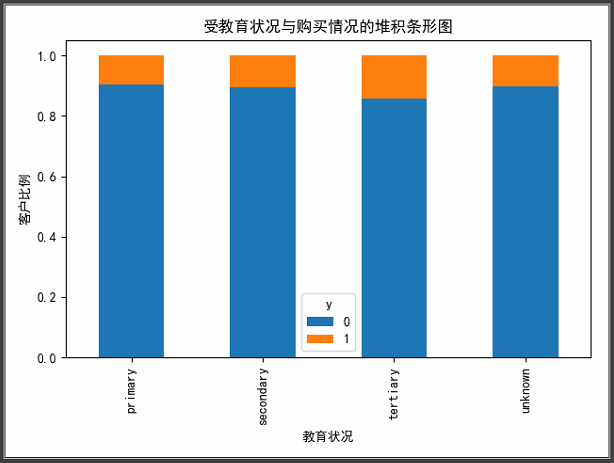
由上图可知,受教育状况似乎对客户购买定期存款有着一定的影响力。
1 ''' 2 可视化展示--month( last contact month of year) 3 ''' 4 pd.crosstab(data_bank.month, data_bank.y).plot(kind='bar') 5 plt.title("每月的购买频率") 6 plt.xlabel("月份") 7 plt.ylabel("购买频率") 8 plt.show()

由上图可以看出,month是一个良好的预测指标。
1 ''' 2 可视化展示--poutcome(先前营销活动的结果) 3 ''' 4 pd.crosstab(data_bank.poutcome, data_bank.y).plot(kind='bar') 5 plt.title("先前营销的购买结果") 6 plt.xlabel("先前营销活动的结果") 7 plt.ylabel("购买频率") 8 plt.show()
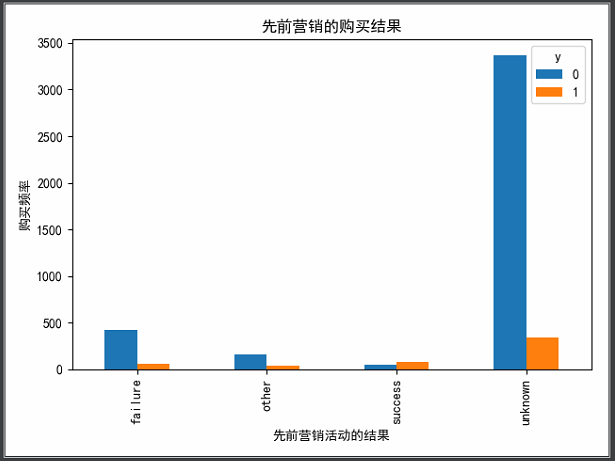
由上图可知,poutcome是一个良好的预测指标。
1 ''' 2 可视化展示--年龄分布 3 ''' 4 data_bank.age.hist() 5 plt.title("年龄直方图") 6 plt.xlabel("年龄") 7 plt.ylabel("人数") 8 plt.show()
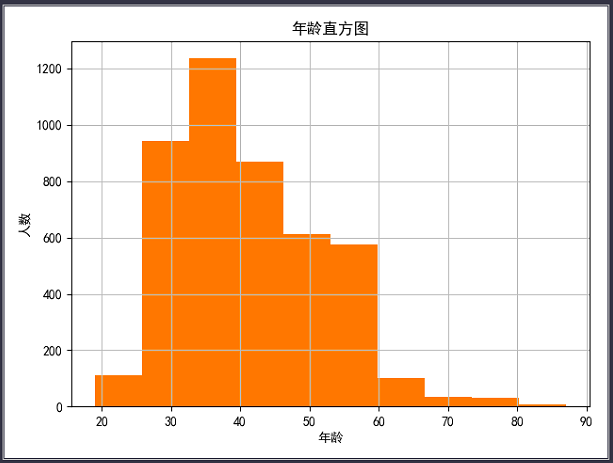
根据上面的直方图可以看出,该数据集中银行的客户年龄集中分布在27~60岁之间。
5.对变量进行处理
1 ''' 2 变量进行one-hot处理 3 ''' 4 variable = ['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'poutcome'] 5 for var in variable: 6 var_list = pd.get_dummies(data_bank[var], prefix=var) 7 bank = data_bank.join(var_list) 8 data_bank = bank 9 data_vars = data_bank.columns.values.tolist() 10 variables = [i for i in data_vars if i not in variable] 11 data_last = data_bank[variables] 12 data_last.columns.values
处理后的数据集字段:
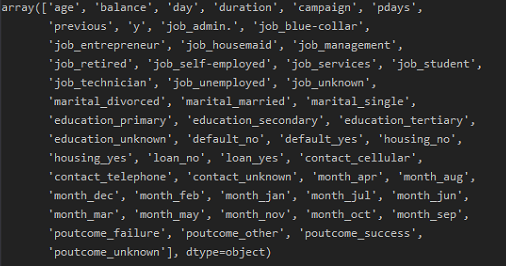
1 ''' 2 分离特征与目标变量 3 ''' 4 data_last_vars = data_last.columns.values.tolist() 5 y = ['y'] 6 X = [i for i in data_last_vars if i not in y] 7 ''' 8 特征选择: 9 在初始特征集上训练估计器,通过coef_属性或通过feature_importances_属性获得每个特征的重要性。 10 从当前的一组特征中删除最不重要的特征。在修剪的集合上递归地重复该过程,直到最终到达所需数量的要选择的特征。 11 ''' 12 from sklearn.linear_model import LogisticRegression 13 from sklearn.feature_selection import RFE 14 15 lg_model = LogisticRegression() 16 rfe = RFE(lg_model, 18) # 递归特征消除 17 rfe = rfe.fit(data_last[X], data_last[y]) 18 print("rfe.support_: ", rfe.support_) 19 print("rfe.ranking_ ", rfe.ranking_) 20 21 # 根据布尔值筛选要的特征 22 from itertools import compress 23 24 cols = list(compress(X, rfe.support_)) 25 print(cols)
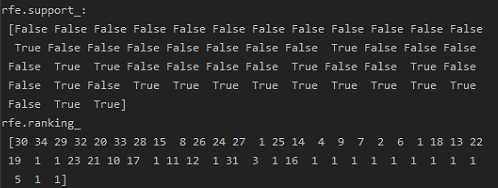
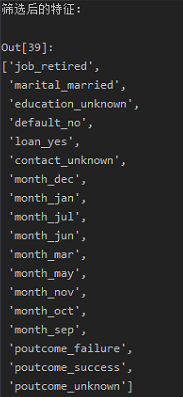
1 # 执行模型 2 import statsmodels.api as sm 3 4 X = data_last[cols] 5 y = data_last[y] 6 logi_model = sm.Logit(y, X) 7 logi_model.raise_on_perfect_prediction = False 8 result = logi_model.fit() 9 print(result.summary().as_text)

大多数变量的p值小于0.05,因此,大多数变量对模型都很重要。
6.逻辑回归模型
1 ''' 2 Logistic Regression模型的拟合 3 ''' 4 from sklearn.model_selection import train_test_split 5 from sklearn.metrics import classification_report 6 from sklearn.metrics import f1_score 7 8 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3) 9 logistic_model = LogisticRegression() 10 logistic_model.fit(X_train, y_train) 11 y_pre = logistic_model.predict(X_test) 12 print("逻辑回归模型的准确率为:", logistic_model.score(X_test, y_test)) 13 print("逻辑回归模型的召回率为: ", classification_report(y_test, y_pre, labels=[0, 1], target_names=['客户不购买定期存款', '客户购买定期存款'])) 14 print("f1-score:", f1_score(y_test, y_pre, average='macro'))
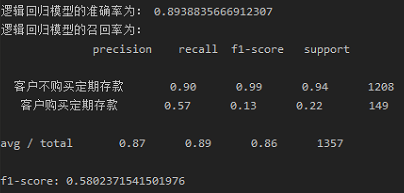
从结果可以看到,在整个测试集中,87%的促销定期存款是客户喜欢的定期存款;89%的客户首选定期存款。
7.交叉验证
1 ''' 2 交叉验证 3 ''' 4 from sklearn import model_selection 5 6 kfold = model_selection.KFold(n_splits=10) 7 modelCV = LogisticRegression() 8 results = model_selection.cross_val_score(modelCV, X_train, y_train, cv=kfold, scoring='accuracy') 9 print("10折交叉验证预测准确率:%.3f" % (results.mean()))

平均精确度非常接近逻辑回归模型的准确度; 因此,可以得出结论,模型很好拟合了数据。
8.ROC曲线验证
1 ''' 2 ROC曲线: 3 ROC曲线是与二元分类器一起使用的另一种常用工具。 4 虚线表示纯随机分类器的ROC曲线; 一个好的分类器尽可能远离该线(朝左上角) 5 ''' 6 from sklearn.metrics import roc_auc_score, roc_curve 7 8 logistic_roc_auc = roc_auc_score(y_test, logistic_model.predict(X_test)) 9 fpr, tpr, thresholds = roc_curve(y_test, logistic_model.predict_proba(X_test)[:, 1]) 10 plt.figure() 11 plt.plot(fpr, tpr, label="Logistic Regression(area = %0.2f)" % logistic_roc_auc) 12 plt.plot([0, 1], [0, 1], 'r--') 13 plt.xlim([0.0, 1.0]) 14 plt.ylim([0.0, 1.05]) 15 plt.xlabel('False Positive Rate') 16 plt.ylabel('True Positive Rate') 17 plt.title('Receiver operating characteristic') 18 plt.legend(loc="lower right") 19 plt.show()
