3.作业要求:
1)贴上视频学习笔记,要求真实,不要抄袭,可以手写拍照。
1)P2 概率论与贝叶斯先验
一、概率论与贝叶斯先验


不管n取值多少,首位数字的分布趋势总是一致。
当1到n!中n=100时,从1~9,出现的各个数字的频率分布折线图:

当1到n!中n=1000时,从1~9,出现的各个数字的频率分布折线图:
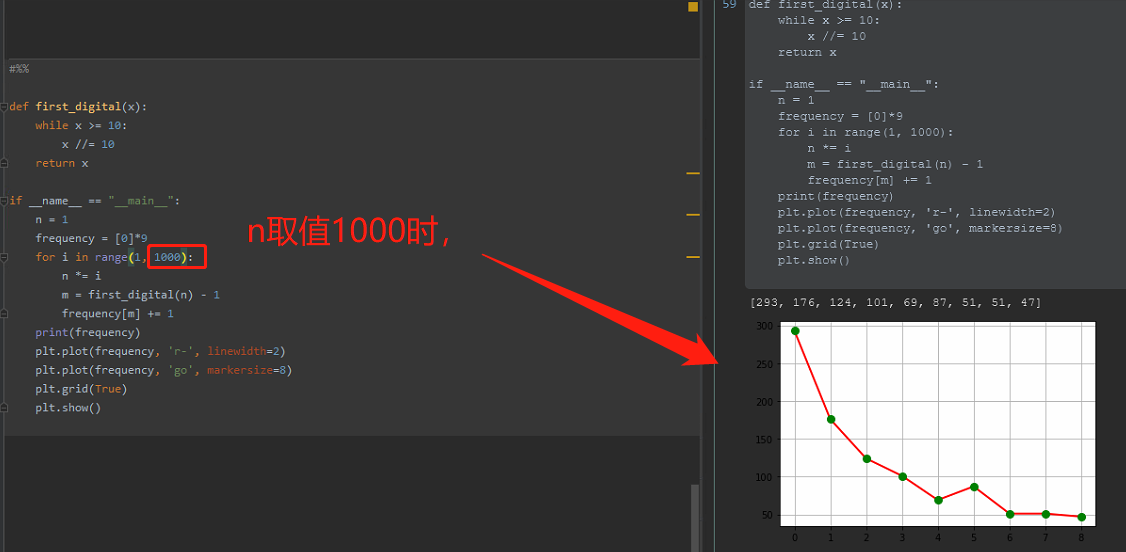
当1到n!中n=10000时,从1~9,出现的各个数字的频率分布折线图:
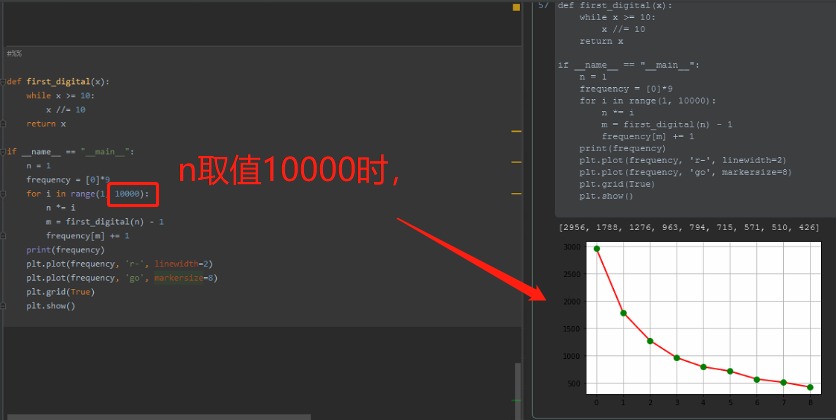
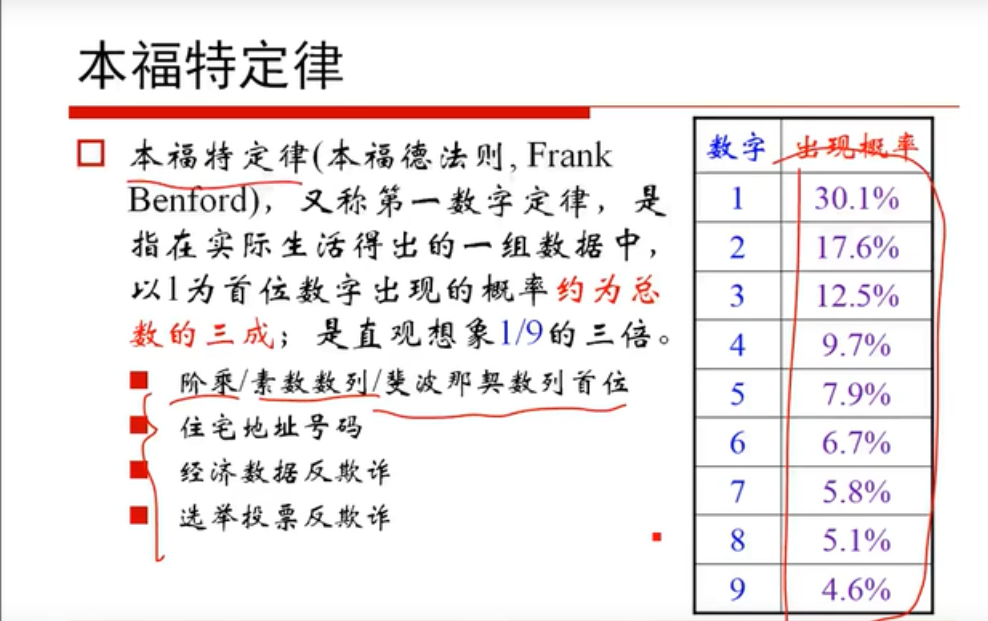
由以上的实验截图说明,在实际生活中得出的一组数据中,以1为首位数字出现的概率约为总数的三成;是直观想象1/9的三倍。
此定律即为“本福特定律”,又称第一数字定律。
举例:
-
商品推荐(阿里笔试题)
-
公路堵车概率模型(Nagel-Schreckenberg交通流模型)


分布:
-
两点分布
-
二项分布(Bernoulli distribution)
-
泊松分布(Poisson distribution)
-
均匀分布
-
指数分布(无记忆性)
-
正态分布(二元正态分布)
- Beta分布
- 指数簇分布
- 伯努利分布(Bernoulli distribution)
- 高斯分布(Gaussian distrubution)






协方差为0定义为不相关。
不相关,说明线性独立。

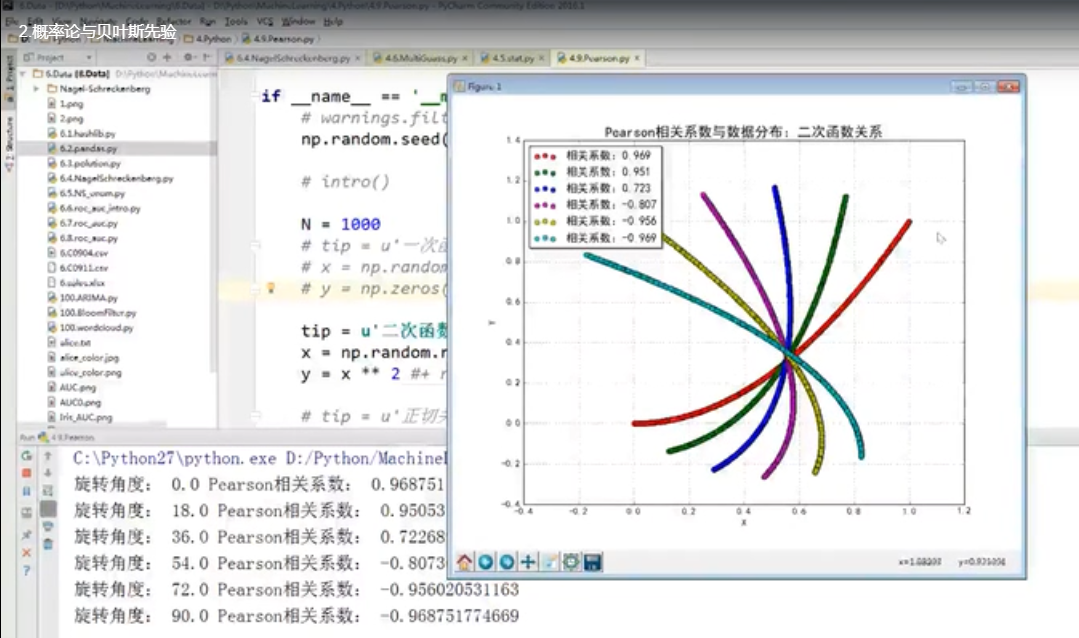

2)P3 矩阵和线性代数
二、矩阵和线性代数
了解SVD
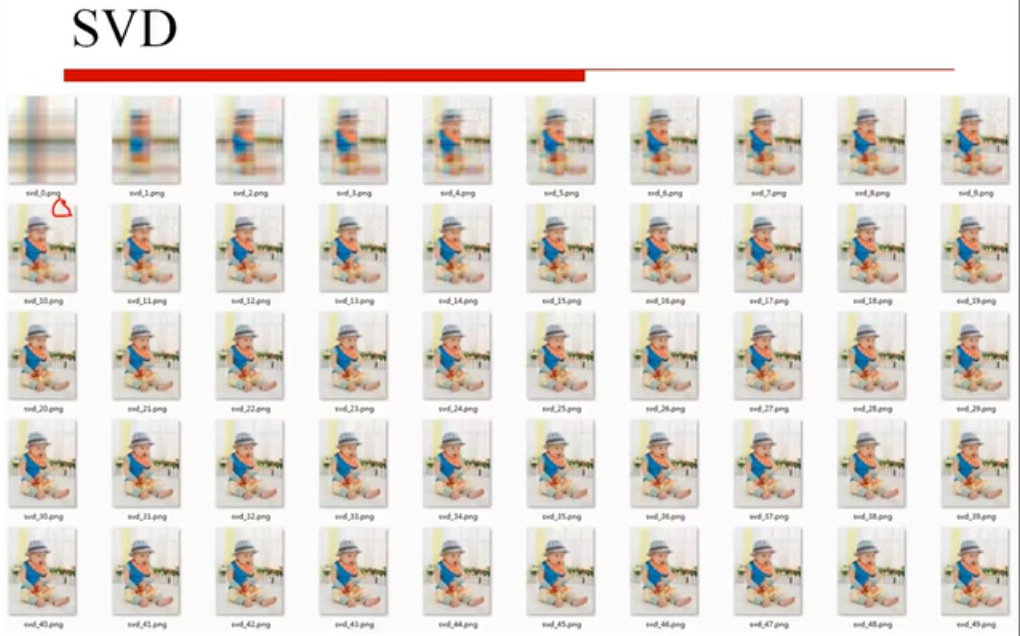

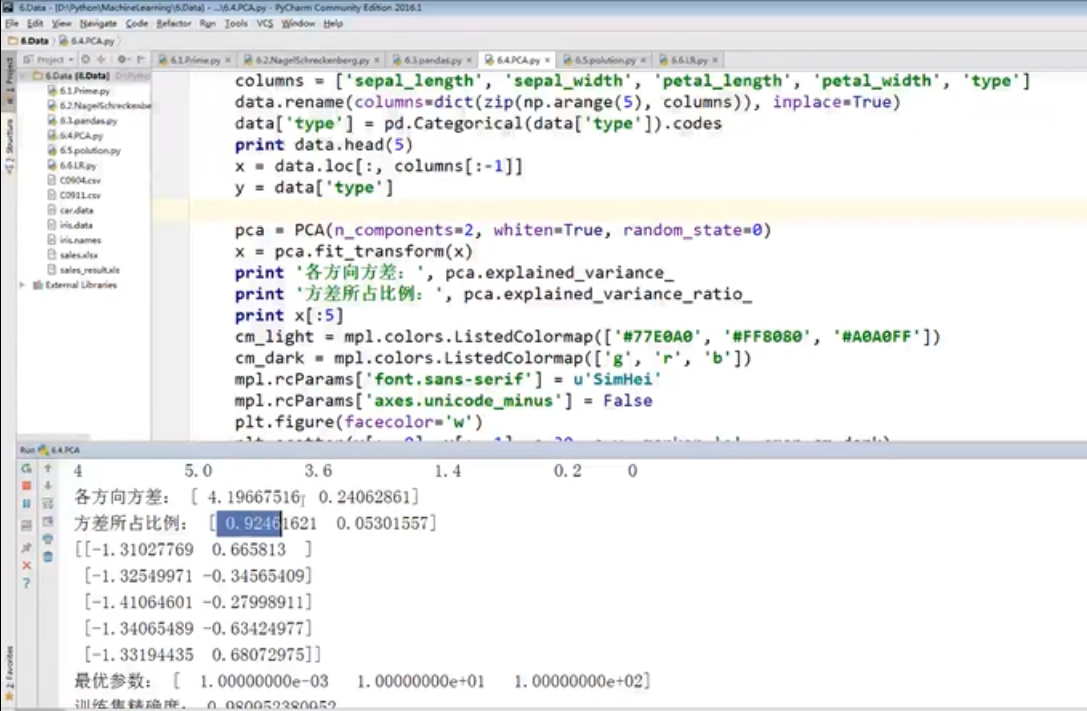

线性代数
- 方阵的行列式
- 代数余子式
- 伴随矩阵
- 方针的逆
- 范德蒙行列式(数学归纳法)
- 矩阵的乘法
- 矩阵模型
- 概率转移矩阵
- 平稳分布
- 矩阵和向量的乘法应用
- 矩阵的秩
- nXn的可逆矩阵,秩为n
- 可逆矩阵又称满秩矩阵
- 矩阵的秩等于它行(列)向量组的秩
- 秩与线性方程组的解的关系
- 向量组等价
- 系数矩阵
- 正交阵

- 特征值和特征向量

- 特征值的性质

- 不同特征值对应的特征向量

- 实对称阵不同特征值的特征向量正交(★)


白化/漂白whitening



- 正定阵(类似还有负定阵,半负定阵)
正定阵的判定:
- 对称阵A为正定阵
- A的特征值都为正
- A的顺序主子式大于0
- 以上三个命题等价

QR分解


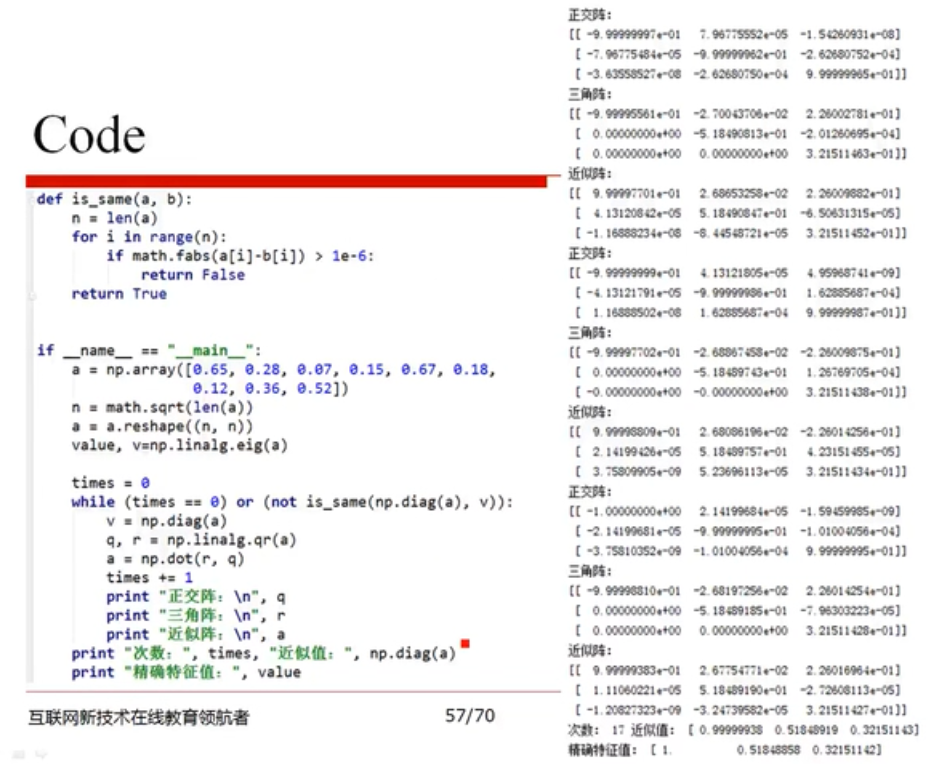


- 向量的导数



- 标量对向量导数

- 标量对方阵的导数
2)用自己的话总结“梯度”,“梯度下降”和“贝叶斯定理”,可以word编辑,可做思维导图,可以手写拍照,要求言简意赅、排版整洁。
一元函数:

y = x 在点 x = 2 处的梯度就是![]()
二元函数:

二元函数求梯度如上图所示。
结论:对多元函数的各个自变量求偏导数,并把求得的这些偏导数写成向量的形式,就是梯度。
- 梯度是一个向量
- 梯度的方向是函数增长最快的方向,梯度的反方向是函数降低最快的方向
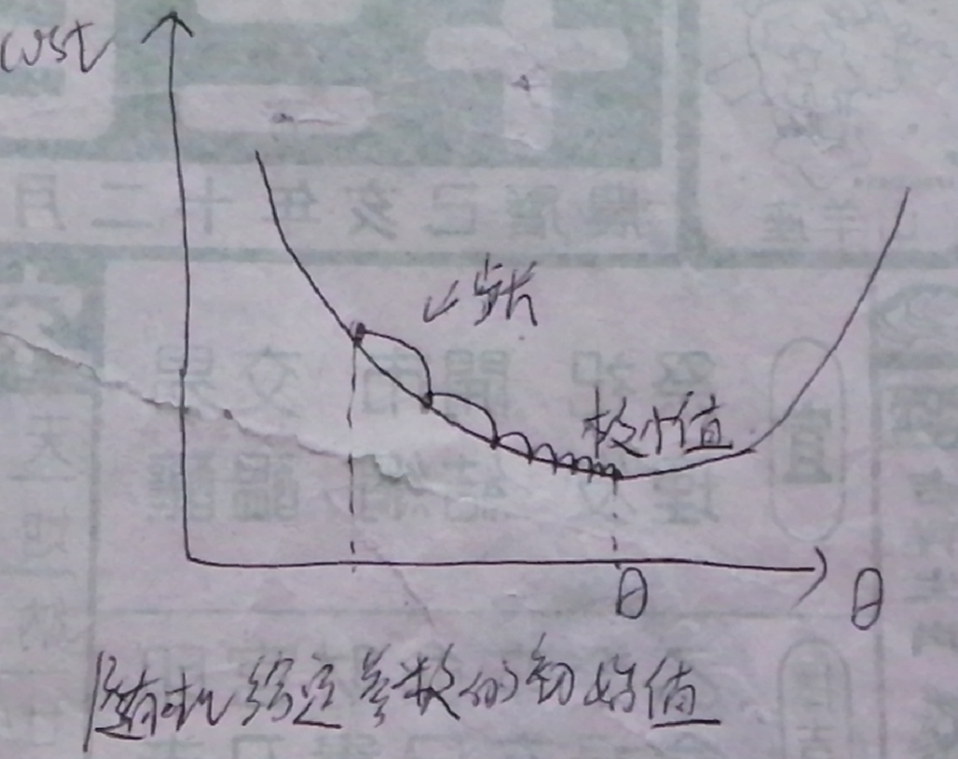
梯度下降
假如攀登一座山峰,从山脚到达顶峰的路径必定有许多条可以选择,如果我想要以最快的方式到达顶峰,我就必须清楚的规划路线,这个时候,我可以利用梯度下降算法来让自己爬到顶峰。具体做法就是我需要根据我当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着最陡峭的方向往上走,同理,下山也如此,只要一直重复这个过程,那么我到达顶峰以及下山的路径,将会是最优路径。
以数学的角度来说,梯度下降算法实际上是一种寻找函数极小值的方法,普遍的做法就是,在已知参数当前值的情况下,按照当前点对应的梯度向量的反方向及事先给定的步长大小,对参数进行调整。
贝叶斯定理
假设有一种疾病的患病率是千分之一,医院一项诊断技术有5%的误诊率(也就是说这5%里面的人没有病但是可能被诊断为有病。。)。
场景:现在有一个人到医院看病,诊断结果也说他有病,那他真的有病是多大的概率?
解题思路是这样子的:
我们普遍人认为的概率:
P(有病)=0.001
P(没病)=0.999
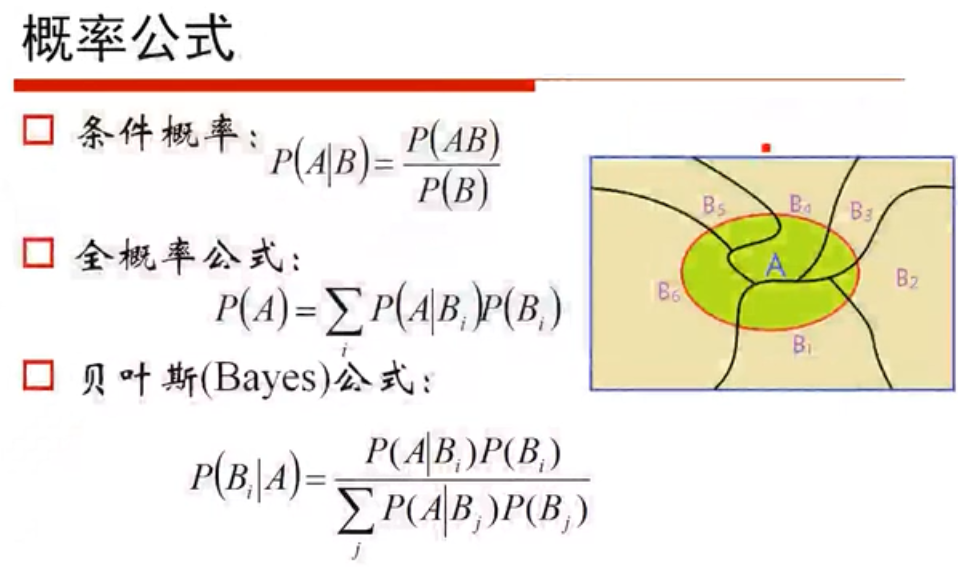
根据贝叶斯定理,实行的条件概率:
P(准确率)=1.00;准确率(患病者100%被检出)。
P(误诊率)=0.05;误诊率(正常人有5%被误检)。
综上,这个人确实患病的概率为:
P(有病 | 阳性) = P(有病) × P(准确率) / [(P(有病) × P(准确率) + P(没病) × P(误诊率)]
= 0.001 × 1.00 / (0.001 × 1.00 + 0.999 × 0.05)
= 0.0198
= 2%
根据结果来看,实际上这个人患病的可能性只有2%,如果体检有问题,还是再去检查一遍看看吧,说不定真没病,嘻嘻。