MDP又称马尔可夫决策过程。
MDP提供了一种结果部分随机部分可控的决策制定框架,具体而言,马尔可夫决策过程是离散时间点的随机控制过程。 在每一步,过程在特定的状态S,而决策者可能选择任何在状态S下可用的行动 a,过程在下一个时间点随机的进入S'状态,并且给予决策者奖励 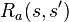 。
。
过程选择行为a 进入  状态的可能性由状态转移函数
状态的可能性由状态转移函数  决定,然而下一个状态S'只依赖于当前状态,而与以前的状态无关,换句话说,马尔科夫决策过程的状态转移具有markov性。
决定,然而下一个状态S'只依赖于当前状态,而与以前的状态无关,换句话说,马尔科夫决策过程的状态转移具有markov性。
马尔可夫决策过程是一个四元组。 其中
其中
 是有限的状态集合
是有限的状态集合 有限行动集合(或者,
有限行动集合(或者,  是在状态s下可以选择的行动的集合),
是在状态s下可以选择的行动的集合),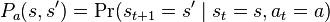 是在状态s下时间点t执行行动a在时间点t + 1进入s'状态的概率。
是在状态s下时间点t执行行动a在时间点t + 1进入s'状态的概率。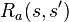 是由状态s到s'的立即回报(或者预期立即回报)。
是由状态s到s'的立即回报(或者预期立即回报)。最主要的问题是如何找到一个策略使总预期回报最大。
选择一个策略

-
 (where we choose
(where we choose 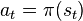 )
) -
当中
 是折扣因子,
是折扣因子, 。
。
下面介绍二种解决算法
其中
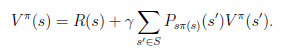
值迭代算法。
|
1、 将每一个s的V(s)初始化为0 2、 循环直到收敛 { 对于每一个状态s,对V(s)做更新 } |
|
2、 循环直到收敛 { } |