常用排序算法
我们通常说的排序都是内部排序,就是数据在内存中进行排序
一种是比较排序,时间复杂度O(nlogn) ~ O(n^2),主要有:冒泡排序,选择排序,插入排序,归并排序,堆排序,快速排序等。
另一种是非比较排序,时间复杂度可以达到O(n),主要有:计数排序,基数排序,桶排序等。

特殊记法:
平均时间复杂度:军训教练说快些以nlog2n的速度归队, 就是快些归队(快排,希尔,归并,堆排)nlog2n
其他的都是O(n2),有个特殊的是基数排序
稳定性:考研复习痛苦啊,情绪不稳定, 快些选一堆好友聊天(快排,希尔,选择,堆)
空间复杂度:快排是O(nlog2n),归并是O(n)基数是O(n+k), 其他都是O(1)
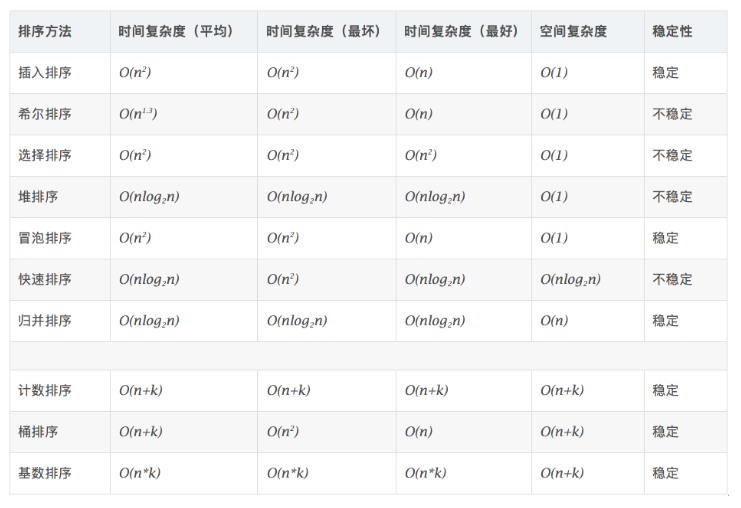
常用排序的比较
算法复杂度
冒泡排序
冒泡排序可以说是最简单的一种排序了,我们学习的第一种排序算法,
排序思想:
- 比较相邻的元素,如果前一个比后一个大,就把它们两个调换位置。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
-
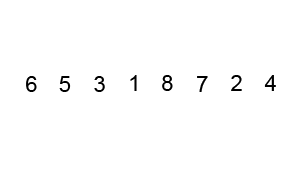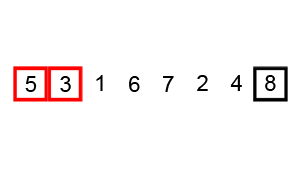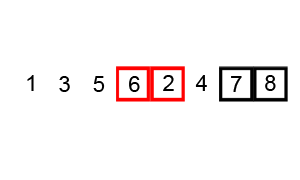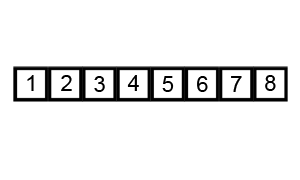
代码:

1 #include <iostream> 2 using namespace std; 3 4 void print(int arr[], int n) 5 { 6 for (int i = 0; i < n; i++) 7 { 8 cout << arr[i]<<" "; 9 } 10 cout << endl; 11 } 12 13 void Swap(int *a, int *b) 14 { 15 int t; 16 t = *a; 17 *a = *b; 18 *b = t; 19 } 20 21 void maoSort(int arr[], int n) 22 { 23 int i, j; 24 for(i = 0; i < n; i++) 25 { 26 for(j = 0; j < n-1-i; j++) 27 { 28 if (arr[j] > arr[j+1]) 29 { 30 Swap(&arr[j], &arr[j+1]); 31 } 32 } 33 } 34 35 } 36 37 int main() { 38 int arr[10] = {1,3,5,7,9,2,4,6,0,-5}; 39 maoSort(arr, 10); 40 print(arr, 10); 41 return 0; 42 }
稳定性:稳定排序。 时间复杂度: O(n)至O(n2),平均时间复杂度为O(n2)。 最好的情况:如果待排序数据序列为正序,则一趟冒泡就可完成排序,排序码的比较次数为n-1次,且没有移动,时间复杂度为O(n)。 最坏的情况:如果待排序数据序列为逆序,则冒泡排序需要n-1次趟起泡,每趟进行n-i次排序码的比较和移动,即比较和移动次数均达到最大值: 比较次数:Cmax=∑i=1n−1(n−i)=n(n−1)/2=O(n2) 移动次数等于比较次数,因此最坏时间复杂度为O(n2)。
插入排序
插入排序是将一个记录插入到已经有序的序列中,得到一个新的元素加一的有序序列, 实际上即将第一个元素看成一个有序的序列,
从第二个元素开始逐个插入得到一个完整的有序序列,插入过程如下:
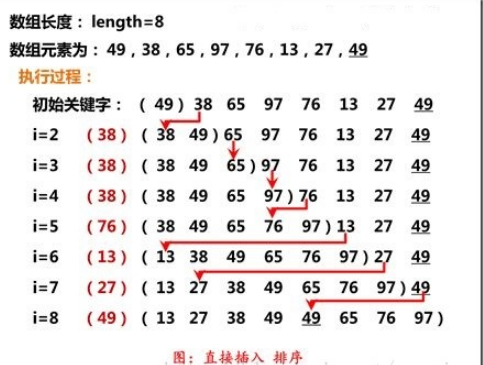
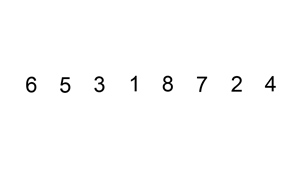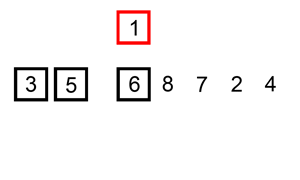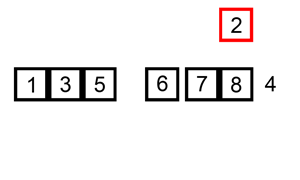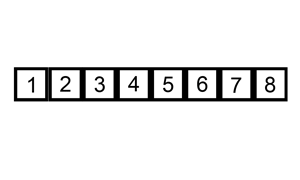

#include <iostream> using namespace std; // 平均时间复杂度 ---- O(n^2) // 所需辅助空间 ------ O(1) // 稳定性 ------------ 稳定 // 思路:每一趟将一个待排序的记录,按照其关键字的大小插入到已经拍好序的一组数据中, // 将第一个看成已经排好序的,然后每次来一个,与前面排好序的进行比较,然后插入。 // 就像打牌一样,每次来一张牌,比较后然后插入进去。 void InsertSort(int arr[], int n) { for (int i = 1; i < n; i++) // 类似扑克牌 排序 { int get = arr[i]; // 右手拿到一张牌 int j = i - 1; // 左手上的牌总是排序好的, while (get < arr[j] && j >= 0) // 将右手的牌与左手的牌 从右向左比较 { arr[j+1] = arr[j]; // 如果左手的牌比抓到的大,将其右移动 j--; } arr[j+1] = get; // 直到左手牌比抓到的牌小(或二者相等),将抓到的牌插入到左手牌右边 // (相等元素的相对次序未变,所以插入排序是稳定的) } } void print(int arr[], int n); int main() { int arr[10] = {1,3,5,7,9,2,4,6,0,-5}; InsertSort(arr, 10); print(arr, 10); return 0; } void print(int arr[], int n) { for (int i = 0; i < n; i++) { cout << arr[i]<<" "; } cout << endl; }
https://www.cnblogs.com/eniac12/p/5329396.html
快速排序
该方法的基本思想是:
1.先从数列中取出一个数作为基准数。
2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
3.再对左右区间重复第二步,直到各区间只有一个数
自己总结的快排思想:
// 思路:先找一个基准(挖坑),然后从后向前找比他小的,然后把这个数填那个(坑)
// 在从前往后找个比他大的,把这个数填进上一个坑,
// 循环一轮后,这个基准就是最终的位置(基准左边都比他小,右边比他大)
推荐博客
https://blog.csdn.net/morewindows/article/details/6684558

#include <iostream> #include <vector> using namespace std; class Solution { // 思路:先找一个基准(挖坑),然后从后向前找比他小的,然后把这个数填那个(坑) // 在从前往后找个比他大的,把这个数填进上一个坑, // 循环一轮后,这个基准就是最终的位置(基准左边都比他小,右边比他大) public: int quick_sort(vector<int>&vec, int left, int right) { int i = left, j = right; int temp; if (left < right) { temp = vec[left]; // 这个循环完成一趟排序,小于temp的数在左边,大于的在右边 while(i < j) { // 从后向前找比temp小的 while(i < j && vec[j] >= temp) --j; if (i < j) vec[i++] = vec[j]; //找到那个比他小的了,把他填在前面坑里 // 从前向后找比temp大的 while(i < j && vec[i] < temp) ++i; // 找到那个比temp大的数,让他填到后面的坑 if (i < j) vec[j--] = vec[i]; } vec[i] = temp; // 把temp放在最终的位置 // 此时i的位置就是temp的位置 quick_sort(vec, left, i-1); // 对temp左边递归调用 quick_sort(vec, i+1, right); //对temp右边递归调用 } } }; int main() { vector<int> vec = {3,5,6,32,35,56,3}; Solution s; s.quick_sort(vec,0, vec.size()-1); for(int i = 0; i< vec.size(); i++) cout << vec[i] << " "; return 0; }
感觉代码乱,这是核心代码

1 int quick_sort(vector<int>&vec, int left, int right) 2 { 3 if (left < right) 4 { 5 int i = left, j = right; 6 int temp = vec[i]; 7 while(i < j) 8 { 9 // 从后向前找比temp小的 10 while(i < j && vec[j] >= temp) 11 --j; 12 if (i < j) 13 vec[i++] = vec[j]; 14 15 // 从前向后找比temp大的 16 while(i < j && vec[i] < temp) 17 ++i; 18 if (i < j) 19 vec[j--] = vec[i]; 20 } 21 22 vec[i] = temp; // 把temp放在最终的位置 23 quick_sort(vec, left, i-1); // 对temp左边递归调用 24 quick_sort(vec, i+1, right); //对temp右边递归调用 25 26 } 27 }
