连续子数组的最大和

HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，你会不会被他忽悠住？(子向量的长度至少是1)

第一眼看到想到的就是暴力解法，把所有的结果都计算出来，但是太复杂了，略了

思路二：一般方法：O(n）

// 思路:用一个maxSum记录累加子数组最大和,用CurSum记录当前累加数组和
//当前累加子数组之和如果大于0就继续累加，如果小于0就剔除原来的累加和，重新开始

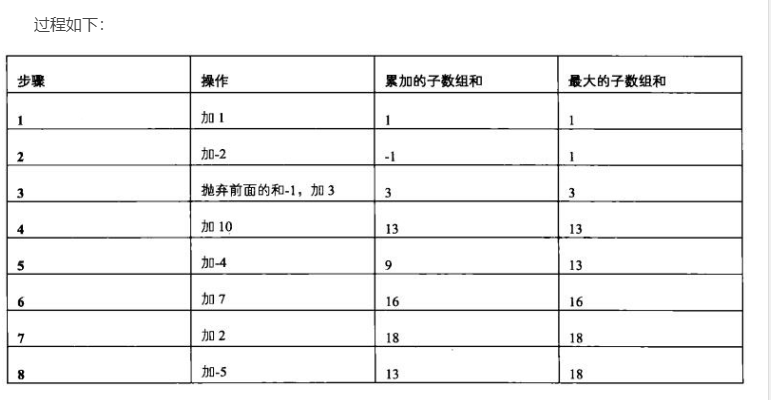
我们对{1,-2,3,10,-4,7,2,-5}进行分析

 代码：

#include <iostream>
#include <vector>
using namespace std;
// 思路:用一个maxSum记录累加子数组最大和,用CurSum记录当前累加数组和
//当前累加子数组之和如果大于0就继续累加，如果小于0就剔除原来的累加和，重新开始
class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
 
    int len = array.size();
    if (len <= 0)
        return 0;
    int MaxSum = array[0];
    int CurSum = array[0];
    for (int i = 1; i < len; i++)
    {
        // 如果当前和小于等于0，说明前面是负数，抛弃前面的和重新计算
        if(CurSum <= 0)
        {
            CurSum = array[i];
        }
        else  // 如果没问题，直接累加
            CurSum += array[i];
 
         // 更新最大和
         if(CurSum >  MaxSum)
                MaxSum = CurSum;
    }
    return MaxSum;
 
    }
};
int main()
{
    Solution s;
    vector<int> vec = {1,-2,3,10,-4,7,2,-5};
    cout << s.FindGreatestSumOfSubArray(vec);
    return 0;
}

思路三：动态规划法

状态方程 dp[i] 表示前i个连续子序列的最大和

动态规划思想。状态方程 

max(dp[i])= getMax( max(dp[i-1]) + arr[i], arr[i]) 。

上面式子的意义是：
我们从头开始遍历数组，遍历到数组元素 arr[ i ] 时，
连续的最大的和 可能为 max(dp[i-1]) + arr[i]，也可能为 arr[i] ，
做比较即可得出哪个更大，取最大值。时间复杂度为 n

#include <iostream>
#include <vector>
using namespace std;

class Solution {
public:
    int getMax(int a, int b)
    {
        return a > b ? a:b;
    }
//    max(dp[i])= getMax( max(dp[i-1]) + arr[i], arr[i])
    int FindGreatestSumOfSubArray(vector<int> array)
    {
        int len = array.size();
        if (len <= 0)
            return 0;
        int sum = array[0];
        int max = array[0];
        for(int i = 1; i < len; i++)
        {
            sum = getMax(sum+array[i], array[i]);

            if (sum >= max)
                max = sum;
        }
        return max;
    }
};
int main()
{
    Solution s;
    vector<int> vec = {1,-2,3,10,-4,7,2,-5};
    cout << s.FindGreatestSumOfSubArray(vec);
    return 0;
}