布隆过滤器及其数学推导

目录

• 布隆过滤器
  • 什么是布隆过滤器
  • 原理简介
  • 数学推导
  • 空间占用情况

布隆过滤器

昨天突然看到了一个布隆过滤器的介绍和一些用法，感觉很新奇，也很有意思，刚好趁着周末来写一篇博客。

什么是布隆过滤器

布隆过滤器？难道是这个？E起来，然后阻挡地方的飞行道具并减少伤害？

NO！NO！NO！当然不是这个，一篇技术博客怎么会扯到游戏呢？来来来，让我们先看一下布隆的E技能。

坚不可摧	E	消耗法力：30/35/40/45/50冷却时间：18/16/14/12/10	布隆朝一个方向举起盾牌，持续3/3.25/3.5/3.75/4秒，并使来自目标方向的第一次攻击变得无效。布隆还将拦截敌方的飞行道具，并将它们摧毁，减少30/32.5/35/37.5/40%的后续伤害。在举盾期间，布隆获得10%移动速度加成。

首先，我们设想一个场景，在某次开发中，你被要求你的网站的用户名不能重复，你应该怎么做？第一感觉当然就是将用户名存到数据库中间，然后当用户注册的时候，查看数据库是否存在这个用户名即可。可是，当你的网站用户量很大的时候比如说一亿，查询数据库毋庸置疑是一个耗时的操作，这个时候，你突然想到了哈希表，因为你知道哈希表的查询时间复杂度是O(1)，可是我们可以算一下，一个用户名为四个汉字，一个汉字占用两个字节（Unicode情况下），那么一共有八亿个字节。一共占用763M的内存（这个里面不包括对象占用的空间，也不包括哈希表中浪费的空间），而实际情况占用的空间会比这个多得多。

那么有什么好方法解决这个问题呢？这个就是我们要讲的布隆过滤器。首先我们以布隆的技能来形象的解释下布隆过滤器的优缺点：

• 并使来自目标方向的第一次攻击变得无效：如果布隆过滤器判断数据不存在则数据绝对不存在。
• 布隆还将拦截敌方的飞行道具：这个就是布隆过滤器的特点，数据先经过布隆过滤器，查询数据是否已经存在。如果布隆过滤器判断用户名不存在/或者存在，数据才能够继续向下走。
• 减少30/32.5/35/37.5/40%的后续伤害：在前面的判断中，可以判断数据绝对不存在，但是如果判断数据存在，则数据也可能不存在。
• 技能加点是不能取消的：布隆过滤器只能插入数据，而不能删除数据。

原理简介

布隆过滤器的原理和哈希表的原理有点类似，同样需要使用hash函数，但是在布隆过滤器中，需要使用多个hash函数。布隆过滤器的原理还是比较简单的。

我们有一个位数组bitArray，对，就是一个位数组，长度位m。只存0和1那种。此时我们有一个key，和k个hash函数，因此我们可以得到k个key被hash过后的数。然后我们分别对hash过后的值取余（对m取余）得到x，然后将bitArray中x位置置为1。

原理图片如下所示（图片来源）

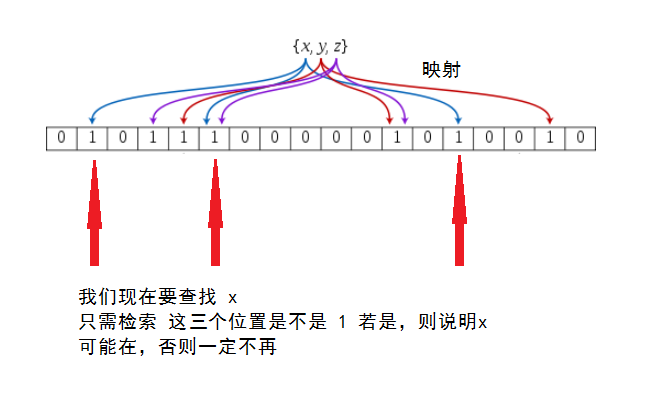
在前面我们介绍过布隆过滤器如果判断数据存在，实际上数据也可能不存在。如果将布隆过滤器应用于垃圾邮件过滤系统，则就会出现“宁可错杀一千，也决不放过一个”的这种情况。那么为什么会造成这种情况呢？实际上，这就和哈希表中哈希冲突的情况一样，因为可能会出现两个key值经过k个hash函数之后，取余之后的结果是一样的。所以，在布隆过滤器中可能会出现误判，所以有一个概念叫做误算率。

数学推导

上面我们知道布隆过滤器中，有一个误算率，当然我们是想将误判降低到最小（key的数量和数组bitArray的长度都是确定的）。so，让我们用数学公式来推导一下。

首先我们有n个key，bitArray的长度位m，hash函数的个数是k，失误率是p（一般很小），推导如下：

1. 误判的概率：

   如果hash函数足够优秀（每一个key都等概率的分配到数组中的某一个位置）。对于一个hash函数来说，bitArray中某个位置被置1的概率是(frac{1}{m})，则不被置1的概率是(1-frac{1}{m})，因为我们有k个hash函数，所以在k个hash函数中，某个位置不被置1的概率是：

   [(1-frac{1}{m})^k ]

   因为插入了n个key，某个位置置1的概率是：（不被置1的概率是((1-frac{1}{m})^{kn})）

   [1-(1-frac{1}{m})^{kn} ]

   如果我们此时去查询某个key是否存在，出现误判（也就是说在bitArray中k个位置都出现了1）的概率是：

   [[1-(1-frac{1}{m})^{kn}]^{k} ]

2. 选择最小的误判概率：

   根据数学知识我们知道：

[ lim_{x ightarrow infty}(1+frac{1}{x})^{x} = e \ 等价于：\ lim_{a ightarrow 0}(1+a)^{frac{1}{a}} = e \ ]

​ 所以：

[[1-(1-frac{1}{m})^{kn}]^{k} = [1-(1-frac{1}{m})^{-mfrac{-kn}{m}}]^{k} = [1-e^{frac{-kn}{m}}]^k ]

​ 然后令(a=e^{frac{-n}{m}}) ,因此概率是：

[f(k)=(1-a^{k})^k ]

我们需要求得便是(f(k))的最小值。对(f(k))进行变换求导：

[egin{align}&f(k) = (1-a^k)^k \&lnf(k) = kln(1-a^k) \&然后进行求导\ &frac{1}{f(k)}f'(k) = ln(1-a^k) - frac{ka^klna}{1-a^k}\&ecause a=e^{frac{-n}{m}} \& herefore a < 1\& herefore 0< f(k)=(1-a^{k})^k <1\&令f'(k) = 0,则 ln(1-a^k) - frac{ka^klna}{1-a^k} =0\& herefore (1-a^k)ln(1-a^k) = ka^klna = a^kln{a^k}\& herefore (1-a^k) = a^k \& herefore a^k = frac{1}{2}\& herefore e^{frac{-nk}{m}} = frac{1}{2} \& herefore frac{nk}{m} = ln2 \& herefore k = frac{mln2}{n} = 0.7frac{m}{n}\&所以误判率p是：\&[1-e^{frac{-kn}{m}}]^k = (1-e^{lnfrac{1}{2}})^{frac{mln2}{n}} \&=(frac{1}{2})^{-ln2frac{m}{n}}\&≈0.6185^frac{m}{n}&end{align} ]

从上面我们可以知道，如果想让误判率一直维持稳定，那么则m和n要维持线性增加。当然，如果是其他变量保持不变，也可以用上面的方法进行求出。

空间占用情况

在这里我们可以很简单的看出来，使用布隆过滤器之后，空间占用率还是蛮低的，还是以上面的例子举例：有一亿个用户，在我们保证保证错误率位0.01%的情况下，我们需要大概19亿位的空间来保存数据（大约是230M的空间）。其中需要的散列函数的个数(k=13)。相比前面还是节省了蛮多的空间。

markdown 写数学公式还是蛮爽的(●'◡'●)