ADMM与one-pass multi-view learning

现在终于开始看论文了，机器学习基础部分的更新可能以后会慢一点了，当然还是那句话宁愿慢点，也做自己原创的，自己思考的东西。现在开辟一个新的模块----多视图学习相关论文笔记，就是分享大牛的paper，然后写出自己的反思，希望大家多多交流。

现在来说说周志华老师的opmv算法。

一摘要

：多视图学习已经成为机器学习非常重要的组成部分，很多得到的效果都比单视图学习要好的多，但是这些方法经常被用在小的和低维的数据集上，主要原因是因为这些算法都占用了，大量的计算内存。最近几年，这些算法有了长足的进步，比如每分钟在youtobe上更新的视频文件中包括视频，音频，和文本文件，要想对如此大的数据量进行分类。传统的多视图学习算法，可能行不通。所以周老师想出了opmv框架---一个不存储整个训练样本集，仅仅完成一次训练。这个方法是通过对不同视图的线性约束复合功能函数进行优化，然后周老师从理论上和经验上对这个算法进行论证。

二介绍

现在越来越多的数据都有两个视图，比如上文说的youtube视频，现在每天的新闻报道可能被写成好几种语言，还有我们以后发表的paper有txt content也有citation linkes。所以说多视图学习会有很大的用武之地的。

然后简要说了一些，多视图的发展历史和最近大牛提出的方法。比如Blum和Mitcgell在1998年提出的co-training算法。

下面我给出co-training算法的工作流程：

Opmv可以看成一个一般形式的在线ADMM优化框架，但是不同点是，以前的ADMM只考虑不变的线性约束，而opmv考虑的是可变的线性约束，比如Y=X+B,以前B是常数，先在变成Y=X+T，T是自变量，所以可以说：opmv包括ADMM?当然这是我猜测，所以不好说。哈哈。。关于ADMM我这里作个补充：

一：ADMM为Alternating Direction Method of Multipliers 交替方向乘子法的缩写，主要是为了求解大规模分布式凸优化问题。

二 凸函数。

2.1形如f(ax+by)<=af(x)+bf(y) 的f(X)函数 其中a+b=1。

2.2 凸函数表达式

    

三：ADMM求解最优化问题

    Min     f(X)+g(Z)

    s.t.    Ax+Bz=C,

        X∈C₁ z∈C₂

其中x∈Rⁿ,z∈R^m,且A∈R^P*n,B∈R^P*m C∈R^P,f(X)和g(X)都是属于凸函数。C₁ C₂属于非空集合。那么我们如何求解这个最优化问题呢，很多人说用拉格朗日乘子法吧，但是经过很多大牛的验证啊，乘子法没有我们下面说的优化方法好，下面我们来看看增量拉格朗日函数。

3.1增量拉格朗日函数

式子如下：

这其实就是在拉格朗日乘子法的基础上加了一个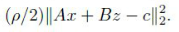其中p是惩罚系数，||Ax+Bz-C||₂²是Ax+Bz-C向量的长度范数，就是内积相乘，在相加，最后开方。

我们可以把上个式子看成：

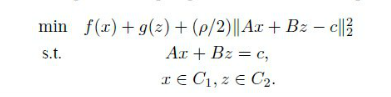
现在可以用迭代的方法分别对这个对偶问题求解：

求解步骤如下：

这样一直迭代下去，直到满足下列条件为止：

其中p和n表示样本的维度和样本量，阈值包含了绝对容忍度（absolute tolerance）和相对容忍度（relative tolerance），这个设置是很烦的，但是貌似大家都认为10-3貌似是比较靠谱的。、

ADMM算法就补充到这里了。

说到这里，one-pass的思想已经说完了，关于推导过程周老师已经推导的很详细了，下面给出他这篇文章的连接，大家自己研究然后互相交流。http://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/acml15opmv.pdf