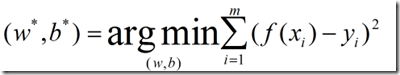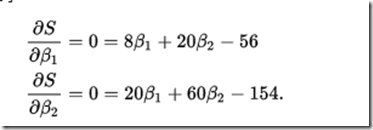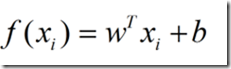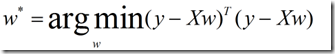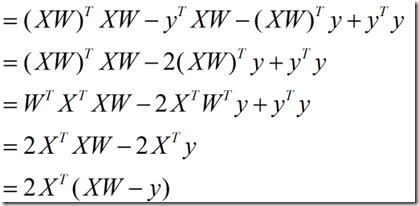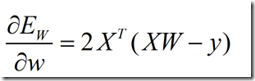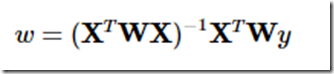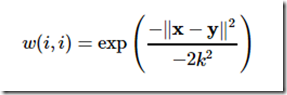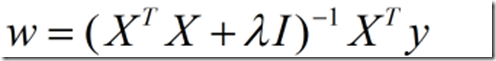机器学习笔记----最小二乘法，局部加权，岭回归讲解

前情提要：关于logistic regression，其实本来这章我是不想说的，但是刚看到岭回归了，我感觉还是有必要来说一下。

一:最小二乘法

最小二乘法的基本思想：基于均方误差最小化来进行模型求解的方法。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小。就是说让你现在追一个女生，你希望女生喜欢你是f(x_i),而女生喜欢你的程度是y_i,你是不是想让你们这两个值相差最少？我们的最小二乘法也是这个原理，但是他引入方差的概念，方差的几何意义对应着欧氏距离。其实大同小异，公式如下：

补充说下维基百科的一个小例子：

某次实验得到了四个数据点（x,y）,分别为（1,6），（2,5），（3,7），（4,10）我们希望找出一条和这四个点最匹配的直线：y=B₁+B₂X, 即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的B₁和B_2：

最小二乘法采用的手段是尽量使得等号两边的方差最小，也就是找出这个函数的最小值：

最小值可以分别求B₁ 和B₂的偏导数，然后使它们等于零得到：

如此就得到了一个只有两个未知数的方程组，很容易就可以解出：

也就是说直线y=3.5+1.4x7yy是最佳的。

好，现在我们接着上面讲，我们的目标是得到：

，且f(x_i)与y_i相差越小越好。

为了方面，我们把b和我w写在一起，构成新的w=(w,b),这个w是一个向量，然后x写成一个矩阵，形如：

再把，样本原先的标记搞成向量模式： ，那么可得出：

可以改编成：

下面我们对w求导。

好像很多人对这种求导公式很烦。我来补充点公式吧。

f(w)	导数
WTX	X
XTW	X
WTX	2W
WTCW	2CW
C是矩阵

求导过程如下：

结果：

当X^TX为满秩矩阵的时候，或者正定矩阵，可得：

所以线性回归模型为：

f(x)=x^TW

下面给出，最小二乘法回归的代码：

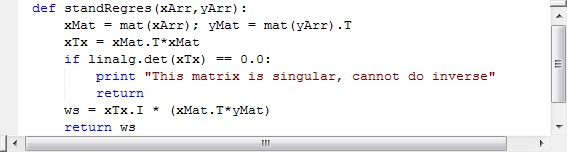
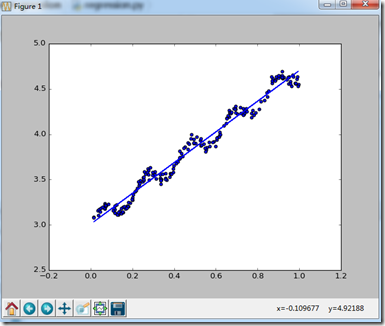
执行效果图：

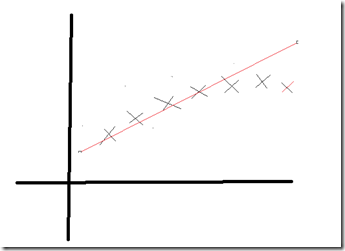
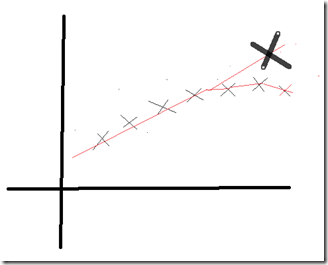
如果单纯的任何情况都用这种线性划分，很容易出现欠拟合现象，什么是欠拟合现象呢，如图：

由上图片可知：最后的几个点，没有拟合在直线上，这就叫做欠拟合现象。那如何解决呢。

二 局部加权线性回归

思路：如果要想解决这个问题，是不是这样就可以了，如下图：

既然方向已经明确，那么来解决问题。

要想解决上述问题，我们可不可以给每个点加一个权重，让这些权重去影响本来的直线，改变他们的方向。该算法给出的回归系数如下：

，W是一个矩阵，是为了给每个点赋予权重。

那估计小伙伴会问，这个权重还能让我们自己凭空yy？我可不想yy了。哈哈。

好，那么我们就引入核的概念，说白了，就是对附近的点让他有更高的权重，这里的核，我们在以后接着svm慢慢和大家说。

最常用的核如下：

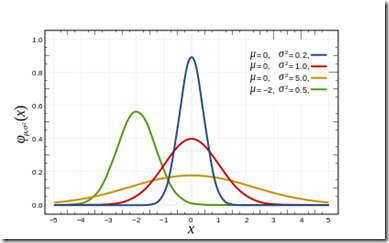
2.1高斯核

高斯核权重：

高斯核分布如下：

2.2 其他核函数，暂时就不赘述了，内容太多，等我另外开一章节再讲。

2.3用高斯核对w进行赋值，

代码实现如下：

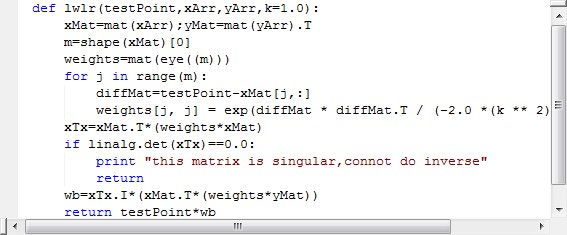
2.4效果图：

感觉效果还行。注意那个K参数，不容易选择，以我现在的水平，我都是试着给的，等我水平上升了，我在来和大家说，哈哈。互相进步，互相伤害啊。

三 岭回归

回去看，是不是我给的代码中总有这样一段：

这句话用数据来说，就是特征比样本还多，所以如果出现这种情况的话，前面的方法，是不是总是print this matrix is singular,cannot do inverse?这是因为X不是满秩矩阵了，不是满秩矩阵不可以求逆，你懂得。

那我们如何解决呢，既然不是，那我们就让他是不就完了吗，现在我们给X^TX加一个矩阵，然后在对这个新的矩阵求逆，不就完了吗。回归系数公式如下：

岭回归是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

本文总结：讲到了最小二乘法，局部加权回归，岭回归这些方法的优缺点，及推导。其实机器学习就这样，给出什么方法，然后为什么用这个方法，这就是算法+优化的过程。送给大家一句话，没有最好的算法，只有适合的算法，要让数据去选择算法。共勉。