AcWing09. 分组背包问题

有(N)组物品和一个容量是(V)的背包。

每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是(v_{ij})，价值是(w_{ij})，其中(i)是组号，(j)是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式
第一行有两个整数(N)，(V)，用空格隔开，分别表示物品组数和背包容量。

接下来有(N)组数据：

每组数据第一行有一个整数(S_i)，表示第(i)个物品组的物品数量；
每组数据接下来有(S_i)行，每行有两个整数(v_{ij}),(w_{ij})，用空格隔开，分别表示第(i)个物品组的第(j)个物品的体积和价值；
输出格式
输出一个整数，表示最大价值。

数据范围
(0<N,V≤100)
(0<S_i≤100)
(0<v_{ij},w_{ij}≤100)
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例：
8

---

思路：

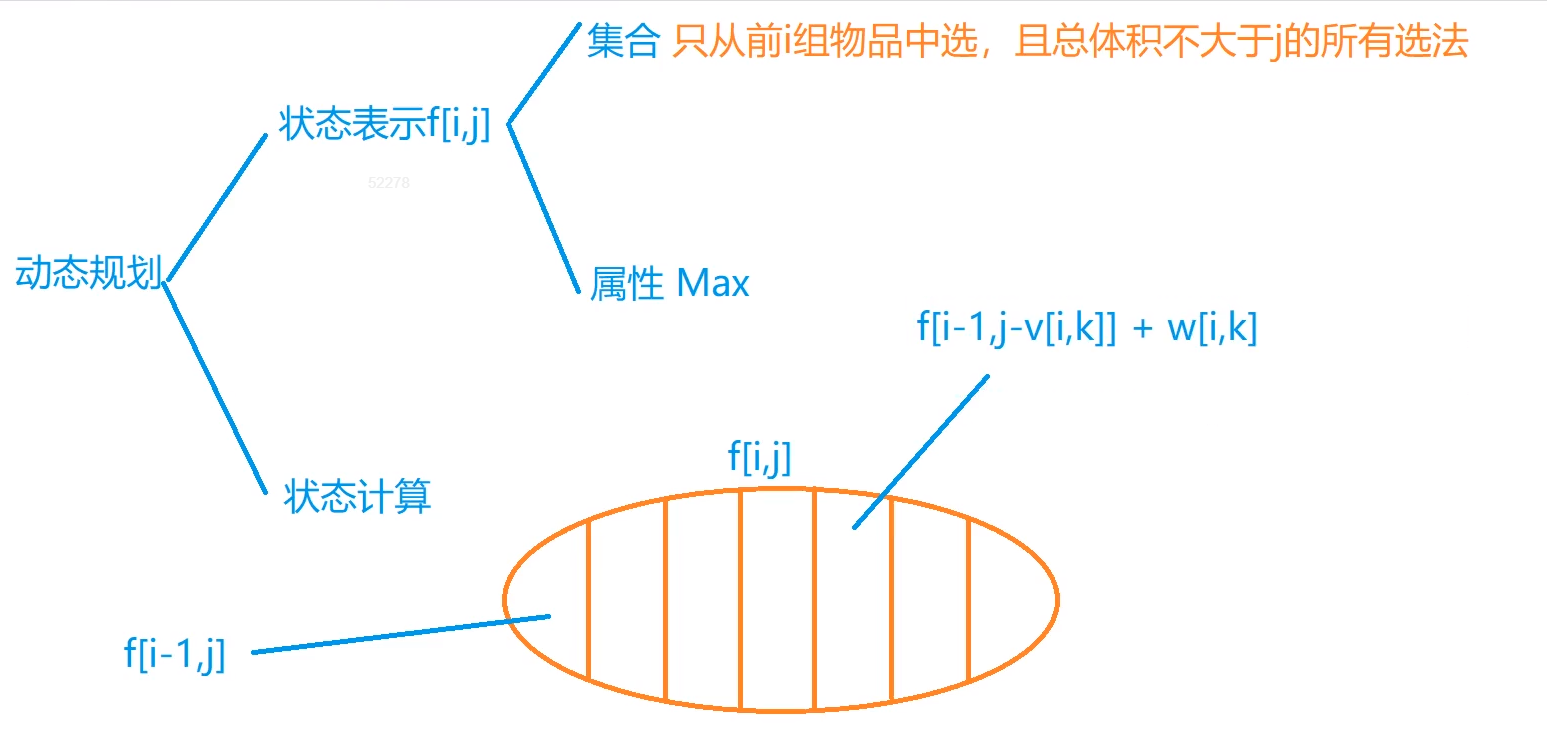
按照如上图所示的方式、对该集合进行集合划分、不难得出、不选(i)的状态表示为(f[i - 1, j])、选(i)的状态表示为(f[i - 1, j - v[i , k]] + w[i , k])，分析过程在我之前的01背包有过类似的
分析、此处不再赘述。指路链接

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int f[N][N], v[N][N], w[N][N];
int s[N];

int main()
{
    int n, m;
    cin >> n >> m;
    
    // input
    for(int i = 1 ; i <= n ; i ++ )
    {
        cin >> s[i];
        for(int j = 0 ; j < s[i] ; j ++ )
            cin >> v[i][j] >> w[i][j];
    }
    
    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = 0 ; j <= m ; j ++ )
        {
            // 不选的情况
            f[i][j] = f[i - 1][j];
            // 选的情况
            for(int k = 0 ; k < s[i] ; k ++ ){
                // 大于的时候才是这个状态
                if( j >= v[i][k])
                {
                    f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
                }
            }
        }
    }
    
    // output
    cout << f[n][m] << endl;
    
    return 0;
}