(一)前缀和算法
概念:前缀和就是数组的前i项之和
一维前缀和
s[1]=a[1]
s[2]=a[1]+a[2]
s[3]=a[1]+a[2]+a[3]
s[4]=a[1]+a[2]+a[3]+a[4]
s[5]=a[1]+a[2]+a[3]+a[4]+a[5]
①.前缀和
输入一个长度为n的整数序列。
接下来再输入m个询问,每个询问输入一对l, r。
对于每个询问,输出原序列中从第l个数到第r个数的和。
输入格式
第一行包含两个整数n和m。
第二行包含n个整数,表示整数数列。
接下来m行,每行包含两个整数l和r,表示一个询问的区间范围。
输出格式
共m行,每行输出一个询问的结果。
数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例:
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例:
3
6
10
#include<iostream> using namespace std; int main() { int sum,n,i,j,x,m,l,r; int s[100009]; cin>>n>>m; sum=0; for(i=1;i<=n;i++) { cin>>x; sum+=x; s[i]=sum; } for(i=0;i<m;i++) { cin>>l>>r; cout<<s[r]-s[l-1]<<endl; } return 0; }
在做题中我们会经常用到他的二维的前缀和数组
最常见的案例:求子矩阵的和
2.子矩阵的和
输入一个n行m列的整数矩阵,再输入q个询问,每个询问包含四个整数x1, y1, x2, y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数n,m,q。
接下来n行,每行包含m个整数,表示整数矩阵。
接下来q行,每行包含四个整数x1, y1, x2, y2,表示一组询问。
输出格式
共q行,每行输出一个询问的结果。
数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例:
17
27
21
对于二维前缀和问题,首先我们先求出他的前缀和数组,如何求呢?
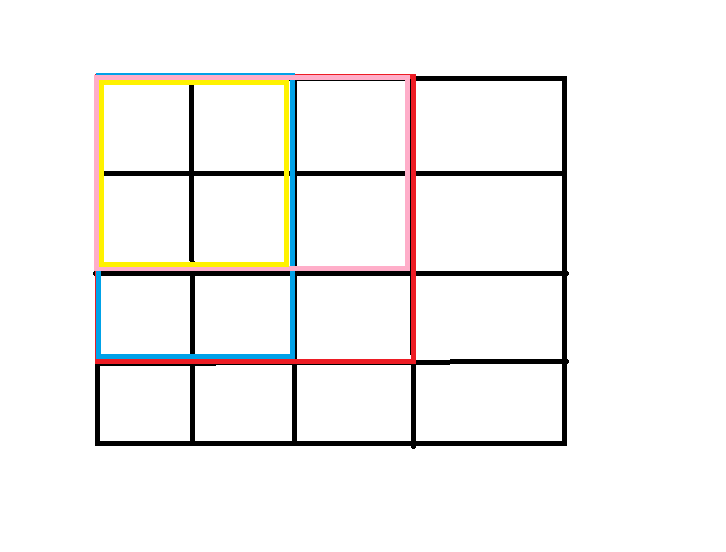
对于(i,j)该点的前缀和数组求解:看图,求红色部分的前缀和
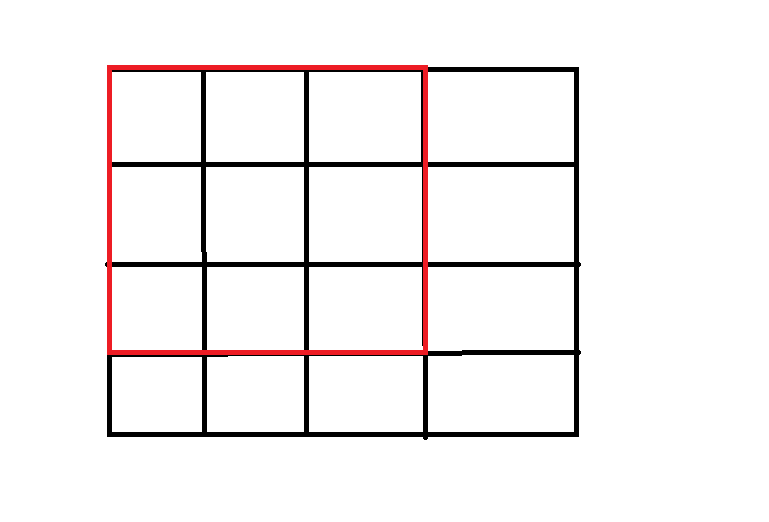
就可以看成是蓝色前缀和+粉色前缀和-黄色前缀和+自己本身
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]
求完前缀和数组后,在分析一下如果要求两个点之间的子矩阵的和应该怎么办?
再画图分析一下:
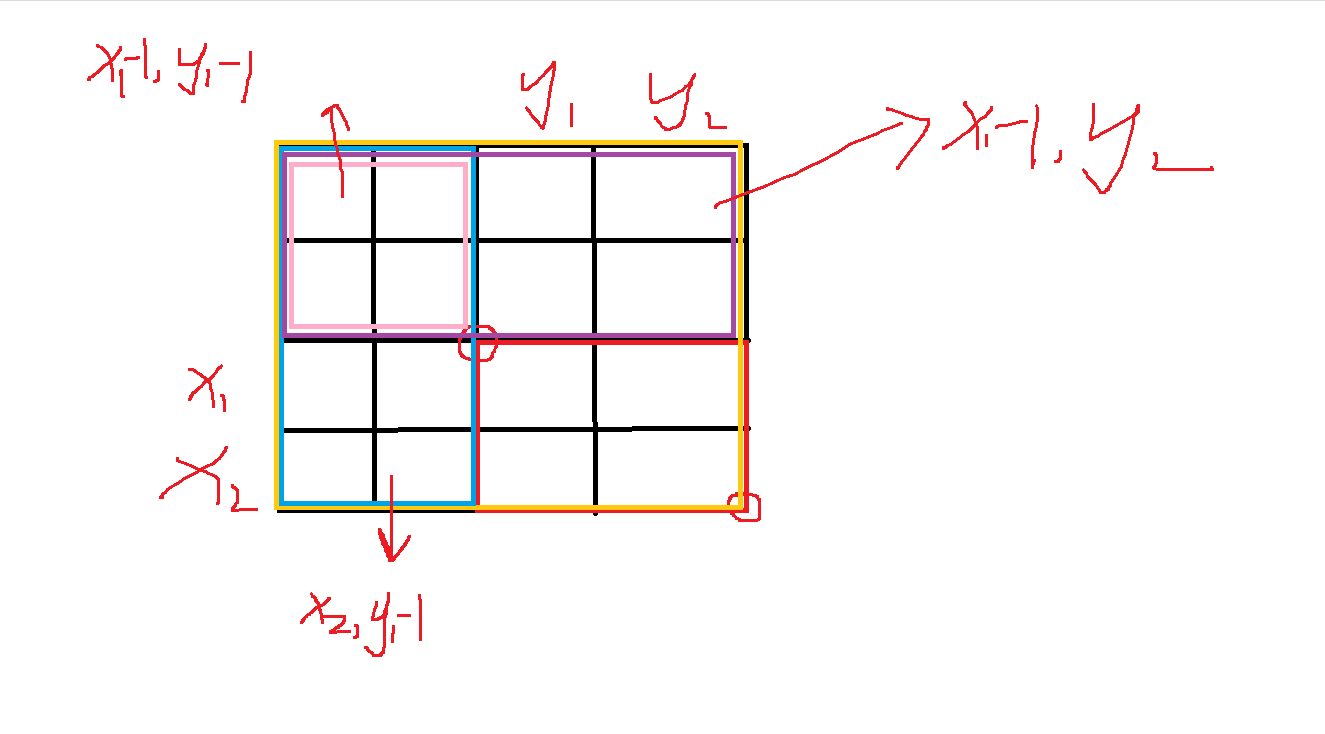
求解两个圆圈之间的子矩阵:黄色面积-蓝色面积-紫色面积+粉色面积
ans=s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]
代码:
#include<iostream> #include<cstdio> using namespace std; int n,m,q,x1,x2,y1,y2; int s[1010][1010],a[1010][1010]; int main() { int i,j; scanf("%d%d%d",&n,&m,&q); for(i=1;i<=n;i++) { for(j=1;j<=m;j++) { scanf("%d",&a[i][j]); s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]; } } while(q--) { scanf("%d%d%d%d",&x1,&y1,&x2,&y2); printf("%d ",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]); } return 0; }