今天,阳光正好,适合敲代码,诸事皆宜。
先来两道简单的模拟题。
第一道
机器翻译
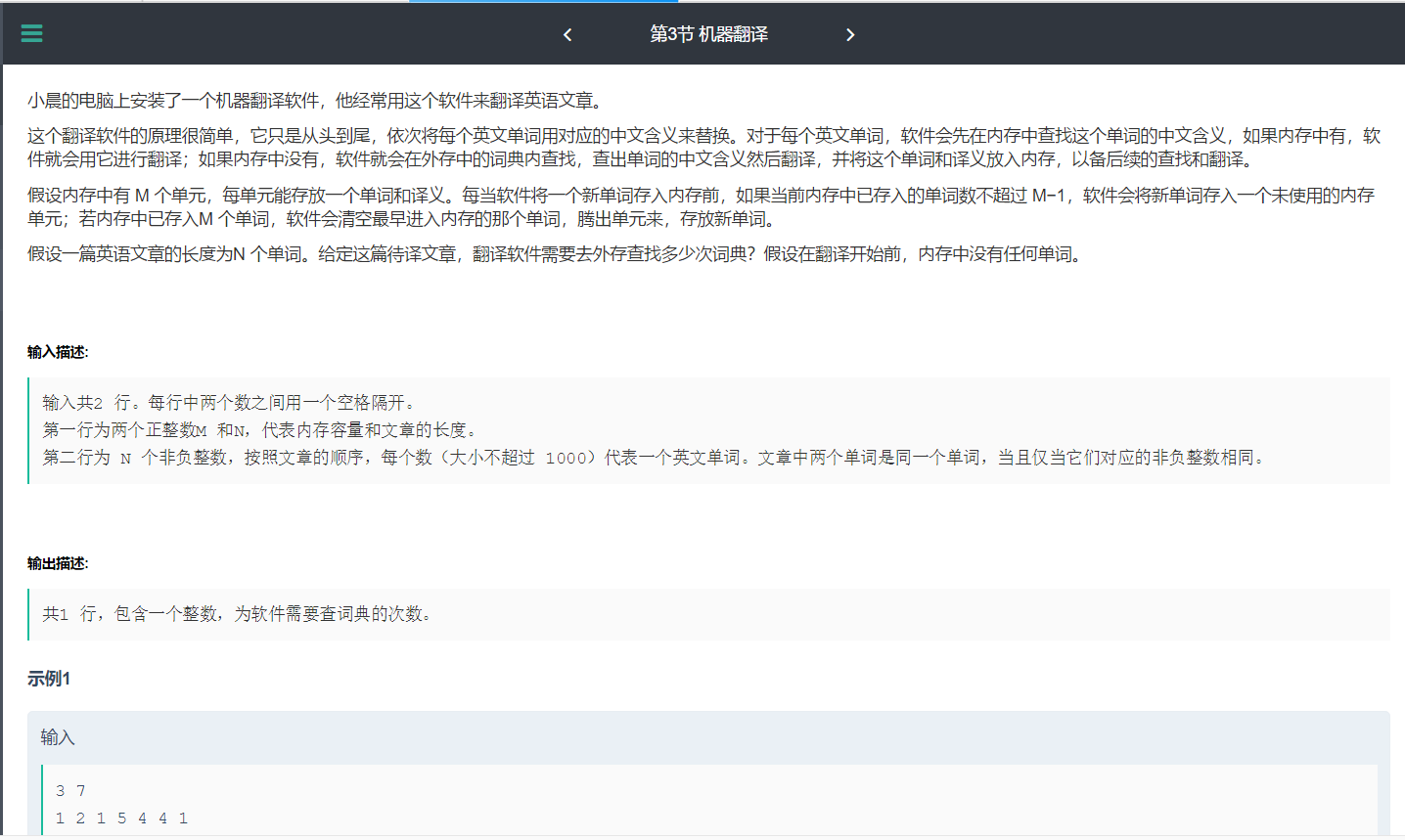
输出为5.
代码思路:很明显需要用到队列来存单词,在建立一个bool数组来存储队列中有没有这个单词,需不需要向外界查询,如果需要并且队列可以容下,则加入队列并将bool数组标记在队列中有该单词,如果队列容不下,则将队头弹出,并用bool数组标记弹出的数字在该队列中没有。
代码:
#include<bits/stdc++.h> using namespace std; queue<int> ss; bool mp[1010]; int n,m; int main() { int i,j,t,ans=0; cin>>m>>n; for(i=0;i<n;i++) { cin>>t; if(ss.size()>m) { int f=ss.front(); mp[f]=0; ss.pop(); } if(mp[t]==0) { ss.push(t); ans++; mp[t]=1; } } cout<<ans<<endl; return 0; }
第二道
神奇的幻方
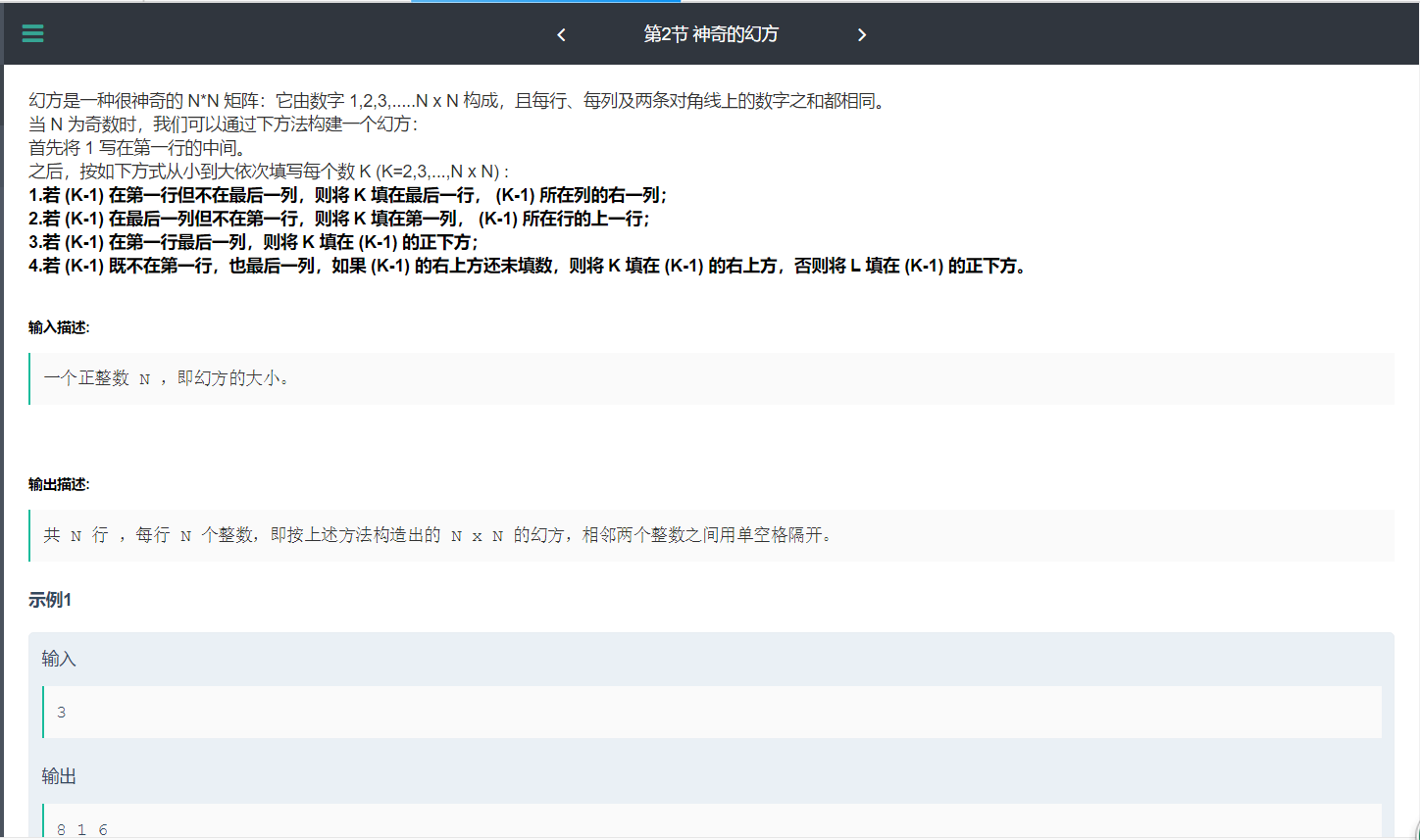
输出为:
8 1 6 3 5 7 4 9 2
思路:按题中步骤执行即可
首先找到1的位置,他在x=1,y=n/2+1;
然后判断若x在第一行,但不在最后一列,就让下一个数在x=n,y++的位置;
若不在第一行,在最后一列,就让下一个数在x--,y=1的位置;
若在第一行最后一列,就让下一个数在x++,y的位置;
若既不在最后一行也不在最后一列,并且右上方没有数字,则下一个数在x--,y++的位置;
以上四个都不满足就在x++,y的位置;
代码:
#include<bits/stdc++.h> using namespace std; int a[111][111]; int main() { int n,i,j,x,y; cin>>n; x=1;y=n/2+1; for(i=1;i<=n*n;i++) { a[x][y]=i; if(x==1&&y!=n) { x=n;y++; } else if(y==n&&x!=1) { y=1;x--; } else if(x==1&&y==n) { x++; } else if(a[x-1][y+1]==0) { x--;y++; } else x++; } for(i=1;i<=n;i++) { for(j=1;j<=n;j++) cout<<a[i][j]<<" "; cout<<endl; } return 0; }
一道二分的题
灵能探索
链接:https://ac.nowcoder.com/acm/contest/639/A
来源:牛客网
思路:二分边界是从[灵能的最小值,灵能总和],check()函数的书写:循环数组,累加如果大于等于mid的值,则让con++,s=0,继续循环直到结束。判断con的值是否大于等于题中输入的组数,大于返回1,证明mid的值还可以在大,就让l=mid+1,ans=mid,如果con的值不大于,证明mid的值大了,则需要r=mid-1,在进行判断找出合适的mid的值。
代码:
#include<bits/stdc++.h> using namespace std; const long long N=100005; long long n,k,ans,a[N]; long long check(long long x) { long long i,j,s=0,con=0; for(i=0;i<n;i++) { s+=a[i]; if(s>=x) { con++; s=0; } } if(con>=k) return 1; return 0; } int main() { long long i,j,minx=100005,sum=0; long long l,r,mid; cin>>n>>k; for(i=0;i<n;i++) { cin>>a[i]; minx=min(minx,a[i]); sum+=a[i]; } l=minx;r=sum; while(l<=r) { mid=(l+r)/2; if(check(mid)) { l=mid+1; ans=mid; } else r=mid-1; } cout<<ans<<endl; }
一个乍一看是一道bfs搜索题,然而他却是到递推题。
好心酸。。。。。
过河卒
链接:https://ac.nowcoder.com/acm/contest/639/B
来源:牛客网
先说说bfs的思路:从(1,1)开始搜索,遇到马或者超界就不放入队列里,最后如果队列到达了终点则ans++;
代码:可惜只过了75%的数据
#include<bits/stdc++.h> using namespace std; const int mod=10000007; int n,m,x,y,ans; int xx[2]={1,0},yy[2]={0,1}; int v[1000][1000]; int vis[1000][1000]; struct node { int a,b; }; void bfs(int X,int Y) { vis[X][Y]=1; node t; t.a=X;t.b=Y; queue<node> p; p.push(t); while(!p.empty()) { node g=p.front(); p.pop(); if(g.a==n&&g.b==m) { ans++; continue; } for(int i=0;i<2;i++) { int w=g.a+xx[i]; int l=g.b+yy[i]; if(v[w][l]!=1&&vis[w][l]!=1&&w>=1&&w<=n&&l>=1&&l<=m) { p.push(node{w,l}); } } } return ; } int main() { int i,j; cin>>n>>m>>x>>y; v[x][y]=1; v[x-1][y-2]=1; v[x-2][y-1]=1; v[x-2][y+1]=1; v[x-1][y+2]=1; v[x+1][y-2]=1; v[x+2][y-1]=1; v[x+1][y+2]=1; v[x+2][y+1]=1; bfs(1,1); cout<<ans%mod<<endl; return 0; }
正解:递推dp[i][j]=dp[i-1][j]+dp[i][j-1]
现将马的所有可去的位置用v[][]的二维数组标记上,然后将表格的第一行和第一列dp[][]赋值为1,如果途中遇到马的位置,则停下结束循环,马下面的将不会走故而可以结束循环,最终用二重循环从(2,2)开始计算如果不是马的位置则dp[i][j]=(dp[i-1][j]+dp[i][j-1])%mod,否则dp[i][j]=0;
最终输出dp[n][m]%mod的值,在这里特别声明一定要在计算dp[i][j]的时候也要取mod,因为数字很大容易超限,导致错误。
代码:
#include<bits/stdc++.h> using namespace std; typedef long long ll; const ll mod=10000007; ll n,m,ans,x,y; int x1[9]={0,-2,-1,1,2,2,1,-1,-2}; int yy[9]={0,1,2,2,1,-1,-2,-2,-1}; ll dp[1004][1004]; ll v[1004][1004]; int main() { ll i,j; cin>>n>>m>>x>>y; v[x][y]=1; for(i=1;i<=8;i++) { if(x+x1[i]>=1&&y+yy[i]>=1) v[x+x1[i]][y+yy[i]]=1; } for(i=1;i<=n;i++) { if(v[i][1]==0) dp[i][1]=1; else break; } for(j=1;j<=m;j++) { if(v[1][j]==0) dp[1][j]=1; else break; } for(i=2;i<=n;i++) { for(j=2;j<=m;j++) { if(v[i][j]==0) dp[i][j]=(dp[i-1][j]+dp[i][j-1])%mod; else dp[i][j]=0; } } cout<<dp[n][m]%mod<<endl; return 0; }
ACM之旅仍在继续,加油!!少年